题目链接：12. 整数转罗马数字 - 力扣（LeetCode）

普通版本（模拟）

条件分析：罗马数字由 7 个不同的单字母符号组成，每个符号对应一个具体的数值。此外，减法规则还给出了额外的 6 个复合符号，且输入的数字满足1 <= num <= 3999

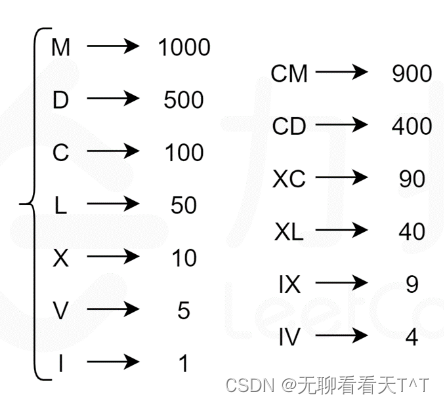
解法分析：为了表示一个给定的整数 num，我们寻找不超过 num 的最大符号值，将 num 减去该符号值，然后继续寻找不超过 num 的最大符号值，将该符号拼接在上一个找到的符号之后，循环直至 num 为 0。最后得到的字符串即为 num 的罗马数字表示

class Solution {
public:string intToRoman(int num) {int values[] = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};string reps[] = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};string res;//最终结果for (int i = 0; i < 13; i++ ){ while(num >= values[i]){num -= values[i];res += reps[i];}}return res;}
};

时间复杂度：O（1）（由于 valueSymbols 长度是固定的，且这 13 字符中的每个字符的出现次数均不会超过 3，因此循环次数有一个确定的上限。对于本题给出的数据范围，循环次数不会超过 15 次）

空间复杂度：O（1）

也是普通版本（硬编码）

由上述内容可得：

千位数字只能由 M 表示
百位数字只能由 C，CD，D 和 CM表示
十位数字只能由 X，XL，L 和 XC 表示
个位数字只能由 I，IV，V 和 IX表示

结论：这恰好把这 13 个符号分为四组，且组与组之间没有公共的符号。因此，整数 num的十进制表示中的每一个数字都是可以单独处理的。

进一步地，我们可以计算出每个数字在每个位上的表示形式，整理成一张硬编码表，利用模运算和除法运算，我们可以得到 num 每个位上的数字（且不违反题目中说的I, X, C, M最多可以附加三次， V、L、D只能被附加一次）：

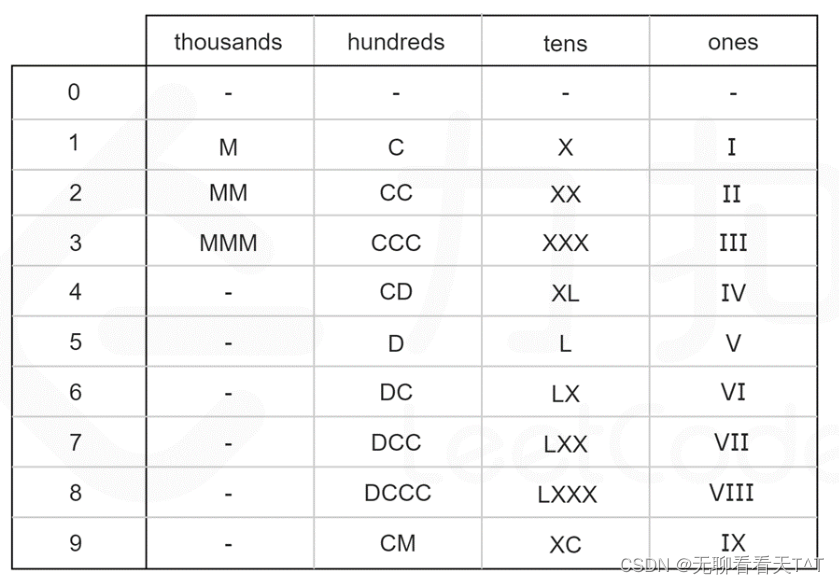
const string thousands[] = {"", "M", "MM", "MMM"};
const string hundreds[]  = {"", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"};
const string tens[]      = {"", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"};
const string ones[]      = {"", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"};class Solution {
public:string intToRoman(int num) {return thousands[num / 1000] + hundreds[num % 1000 / 100] + tens[num % 100 / 10] + ones[num % 10];}
};

时间复杂度：O（1）（由于 valueSymbols 长度是固定的，且这 13 字符中的每个字符的出现次数均不会超过 3，因此循环次数有一个确定的上限。对于本题给出的数据范围，循环次数不会超过 15 次）

空间复杂度：O（1）

~over~