基于STM32的各种数学函数优化计算方法（代码开源）

前言：本文为手把手教学 STM32 的数学计算公式优化方法的教程，本教程的 MCU 使用 STM32F103ZET6 。本篇博客将使用非传统数学库计算手段进行各种数学函数的计算，优化的数学计算包括：sin()、cos()、arctan()、arcsin() 与 1/sqrt()。作为研发的项目产品，实现产品功能往往是很容易的，最重要的核心其实是产品功能的优化，以最优的控制亦或是消耗时间去完成制定的任务，算法优化就是如此。本篇博客将给作者们提供嵌入式工程中常用的数学函数优化代码，希望该博文能给读者朋友的工程项目给予些许帮助（代码开源）。

算法应用平台：STM32F103ZET6；

算法优化情况：

sin() 函数优化：

Q_rsqrt() 函数优化：

一、STM32的数学计算

1.1 STM32数学计算概述

STM32 是 STMicroelectronics 生产的一系列 32 位 ARM Cortex-M 微控制器。它们广泛应用于工业、消费和医疗等领域。STM32 微控制器支持各种数学计算，包括但不限于：

1、算术运算：加法、减法、乘法、除法等基本运算。

2、浮点运算：STM32F系列微控制器支持单精度和双精度浮点运算。

3、三角函数：正弦、余弦、正切等。

4、指数和对数函数：e的x次幂、自然对数、常用对数等。

5、根号和幂运算：平方根、立方根、x的y次幂等。

针对这些数学计算，STM32 通常提供硬件浮点单元 FPU 和一些数学库。使用这些功能可以大大提高计算速度和精度。

本篇博客的数学函数优化与传统 STM32 的 Math 库的数学函数进行对比！！！

1.2 算法优化作用

算法优化是指在保证算法结果正确的前提下，通过改进算法的效率、资源消耗、可读性等方面，使得算法在执行速度、内存使用、能耗等方面得到提升的过程。算法优化的作用主要体现在以下几个方面：

1、提高执行速度：优化算法可以减少不必要的计算步骤，提高算法的执行效率，从而减少程序的运行时间。

2、增强用户体验：在用户界面和交互式应用中，算法优化可以减少等待时间，提高用户体验。

3、提高稳定性：优化算法可以减少程序的出错概率，提高系统的稳定性。

4、提高可维护性：优化后的算法结构更加清晰，逻辑更加简单，便于后续的维护和升级。

5、增强竞争力：在商业应用中，算法优化可以提高产品的性能，增强企业的市场竞争力。

6、节能环保：对于嵌入式系统和移动设备，算法优化可以减少能耗，延长电池寿命，符合节能减排的要求。

如今，各种项目中都需要涉及到算法优化，包括：巡线小车、送药小车竞赛、电源设计、自动驾驶的智驾、目标追踪与飞行器。

二、STM32使用定时器实现＜获取代码块运算时间＞的功能

2.1 STM32的代码块消耗时间

STM32 的代码都是利用 CPU 进行计算和实现的，故代码每步都需要消耗一定的时间才能完成该指定任务。各种代码亦或是算法需要消耗的时间是完全完全不相同的，本篇博客利用 STM32 的定时器来计算 <代码块的运行时间>，从而判断算法或代码的优劣情况！

统计 <代码块的运行时间> 的手段：(1)、逻辑分析仪；（2）、定时器读取时间；（3）、打断点记录时间；

1、利用逻辑分析仪去统计；

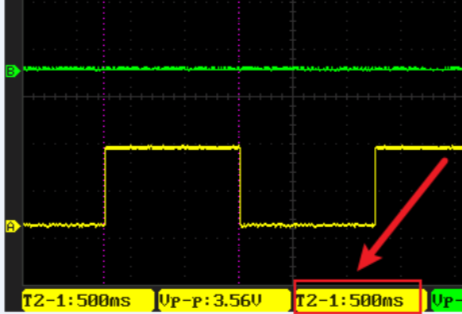
在待测程序段的开始阶段使单片机的一个GPIO输出高电平，在待测程序段的结尾阶段再令这个GPIO输出低电平。用示波器或者逻辑分析仪通过检查高电平的时间长度，就知道了这段代码的运行时间。

while(1){HAL_GPIO_WritePin(GPIOB,GPIO_PIN_1,GPIO_PIN_SET); //PB1置1delay_ms(500);HAL_GPIO_WritePin(GPIOB,GPIO_PIN_1,GPIO_PIN_RESET);	//PB1置0delay_ms(500);
}

延时500ms时波形如下:

修改延时为100ms；

while(1){HAL_GPIO_WritePin(GPIOB,GPIO_PIN_1,GPIO_PIN_SET); //PB1置1delay_ms(100);HAL_GPIO_WritePin(GPIOB,GPIO_PIN_1,GPIO_PIN_RESET);	//PB1置0delay_ms(100);}

波形如下

总结：

使用示波器测量较为准确，缺点是需要单独的示波器或者逻辑分析仪等，示波器一般体积较大的还需要供电，并且还要连接GPIO口，还是有点麻烦的

2、利用定时器读取时间；

利用 TIM2->CNT 与 TIM2 的需要时间来统计代码块消耗的时间；

3、打断点记录时间；

推荐博客地址：http://t.csdnimg.cn/K9fyE

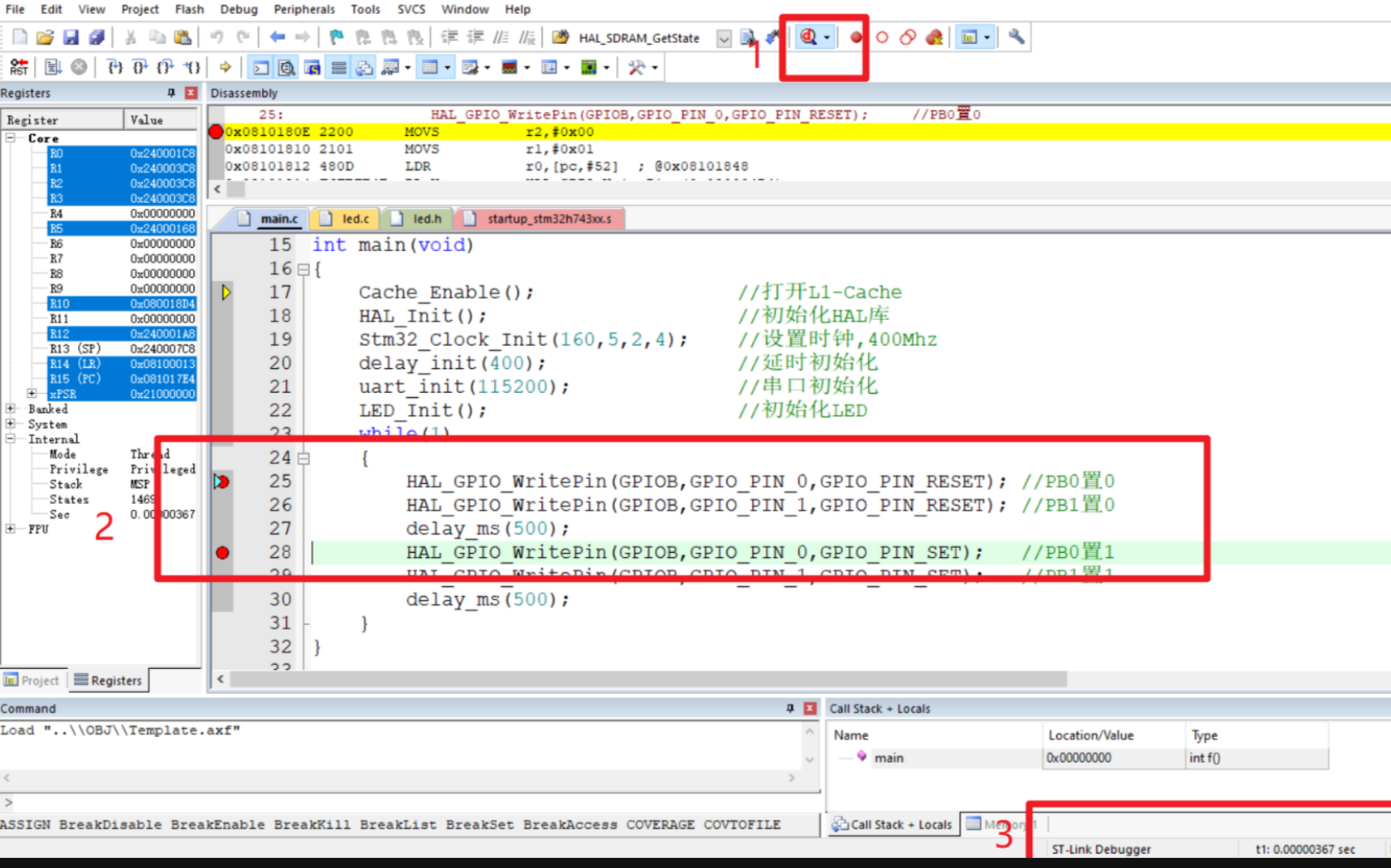
利用J-LINK或者ST-link 等仿真器，实现对代码运行时间的测量，首先要设置仿真器仿真的实际频率；

点击 Settings 设置

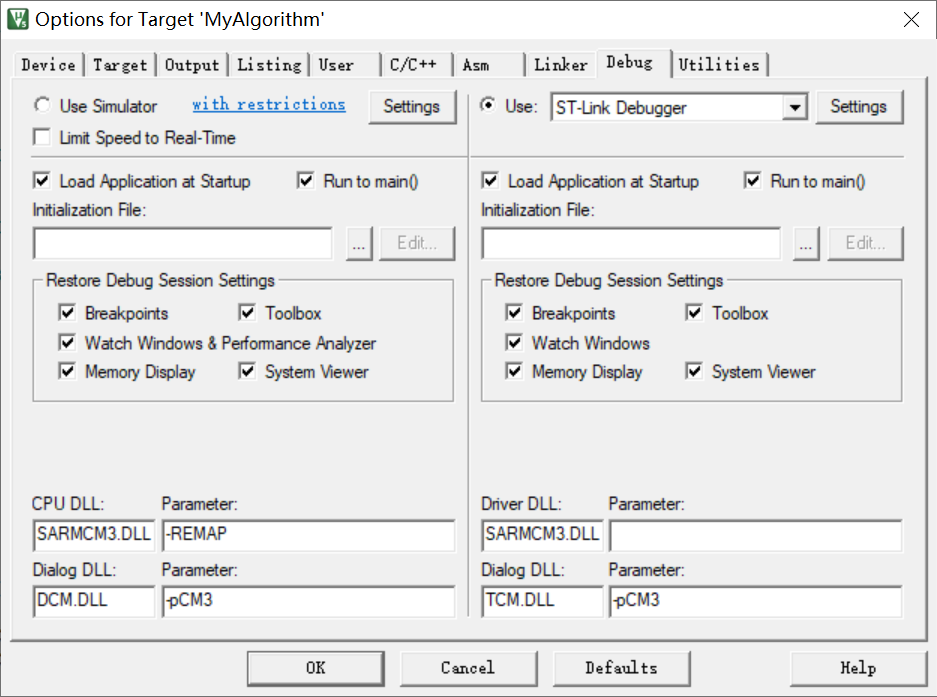
然后点击Trace 设置我们芯片的系统频率，点击Teace Enable 使能

如果工作频率设置不正确，则会造成测量的时间不正确。

仿真器默认采用的是10MHz的工作频率

点击 DEBUG 模式；

2.2 CubeMX配置

本篇博客使用 STM32 的 TIM2 来统计代码块的消耗时间

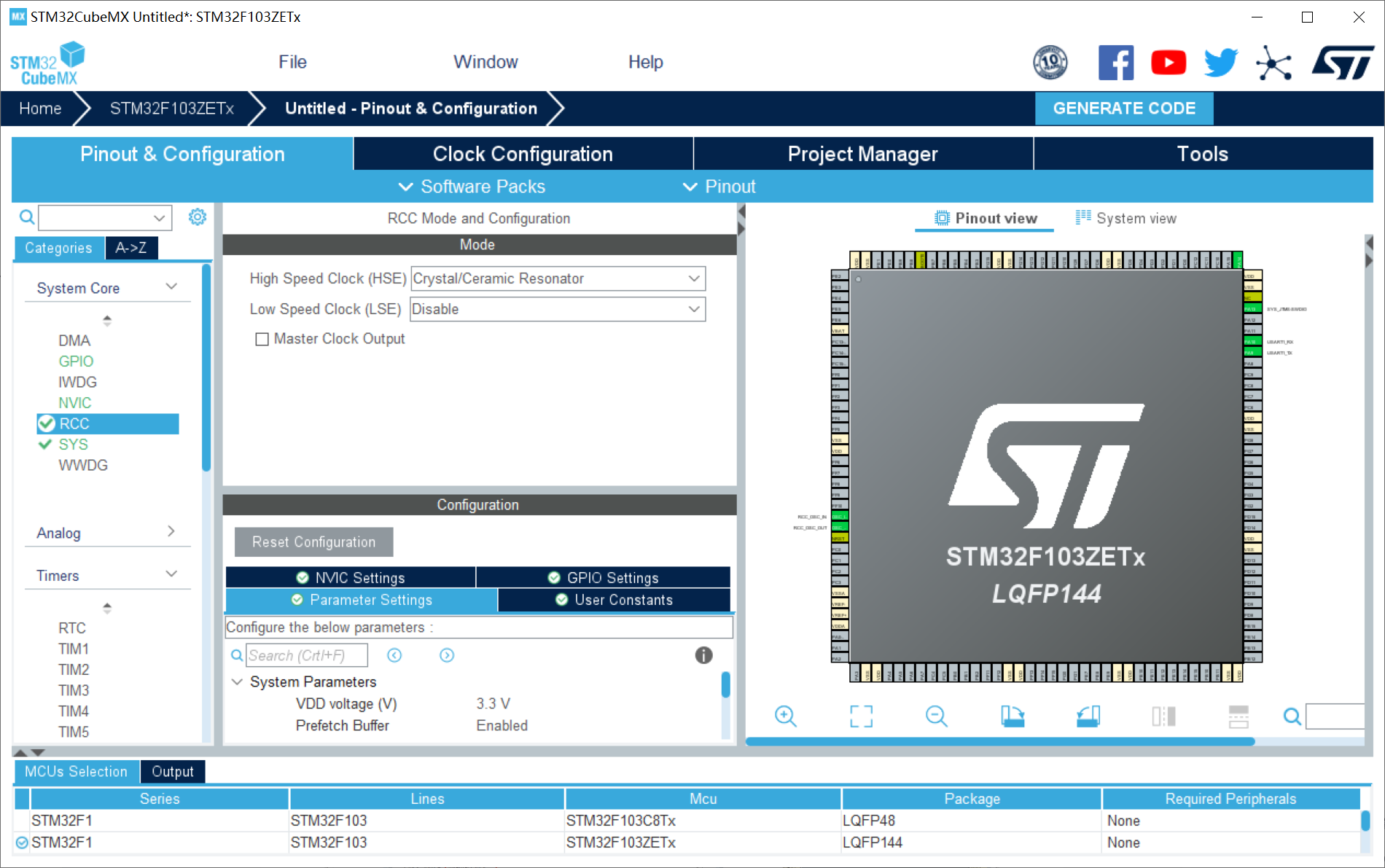
1、RCC配置外部高速晶振（精度更高）——HSE；

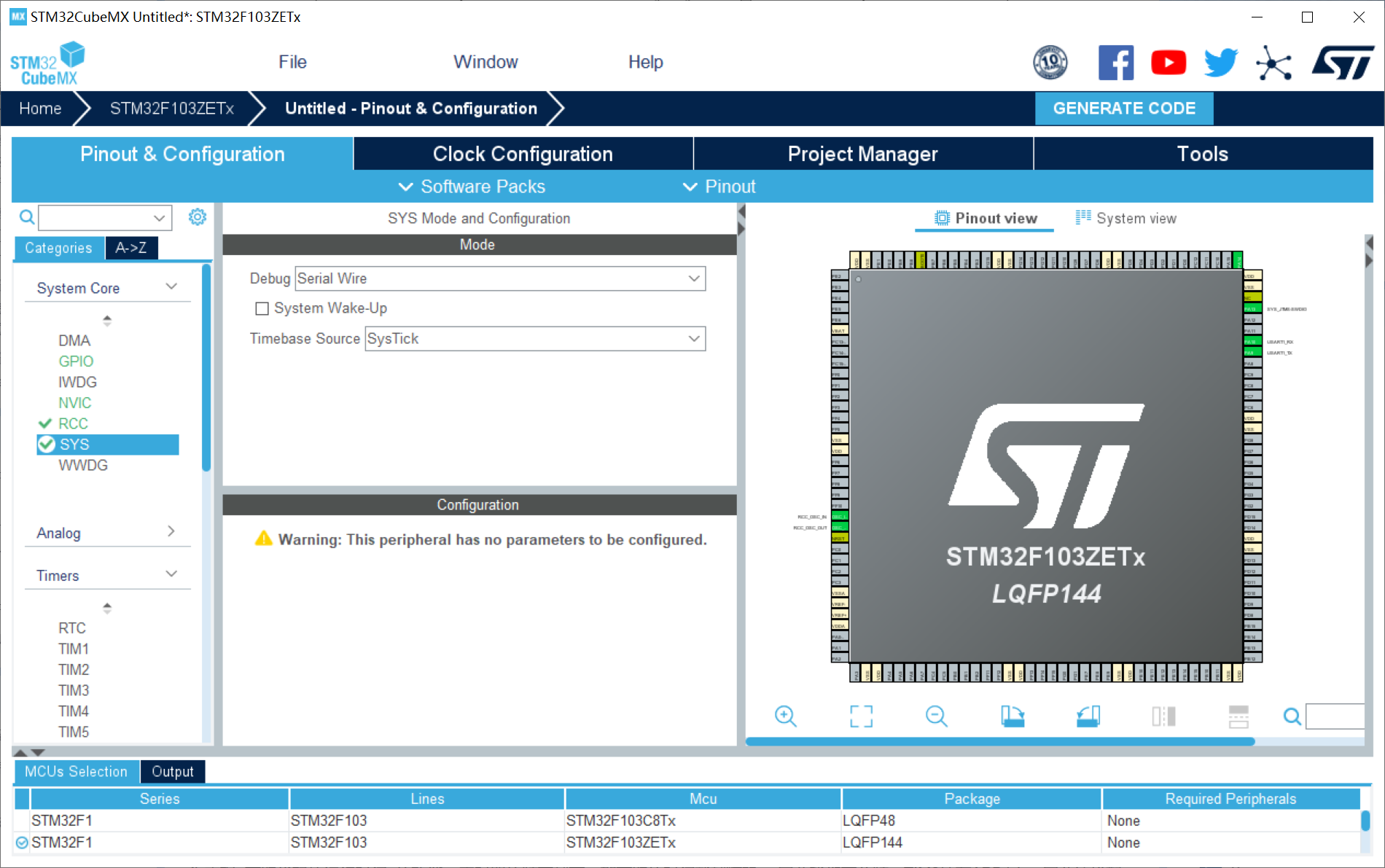
2、SYS配置：Debug设置成Serial Wire（否则可能导致芯片自锁）；

3、TIM配置：利用TIM2来读取代码块的消耗时间；

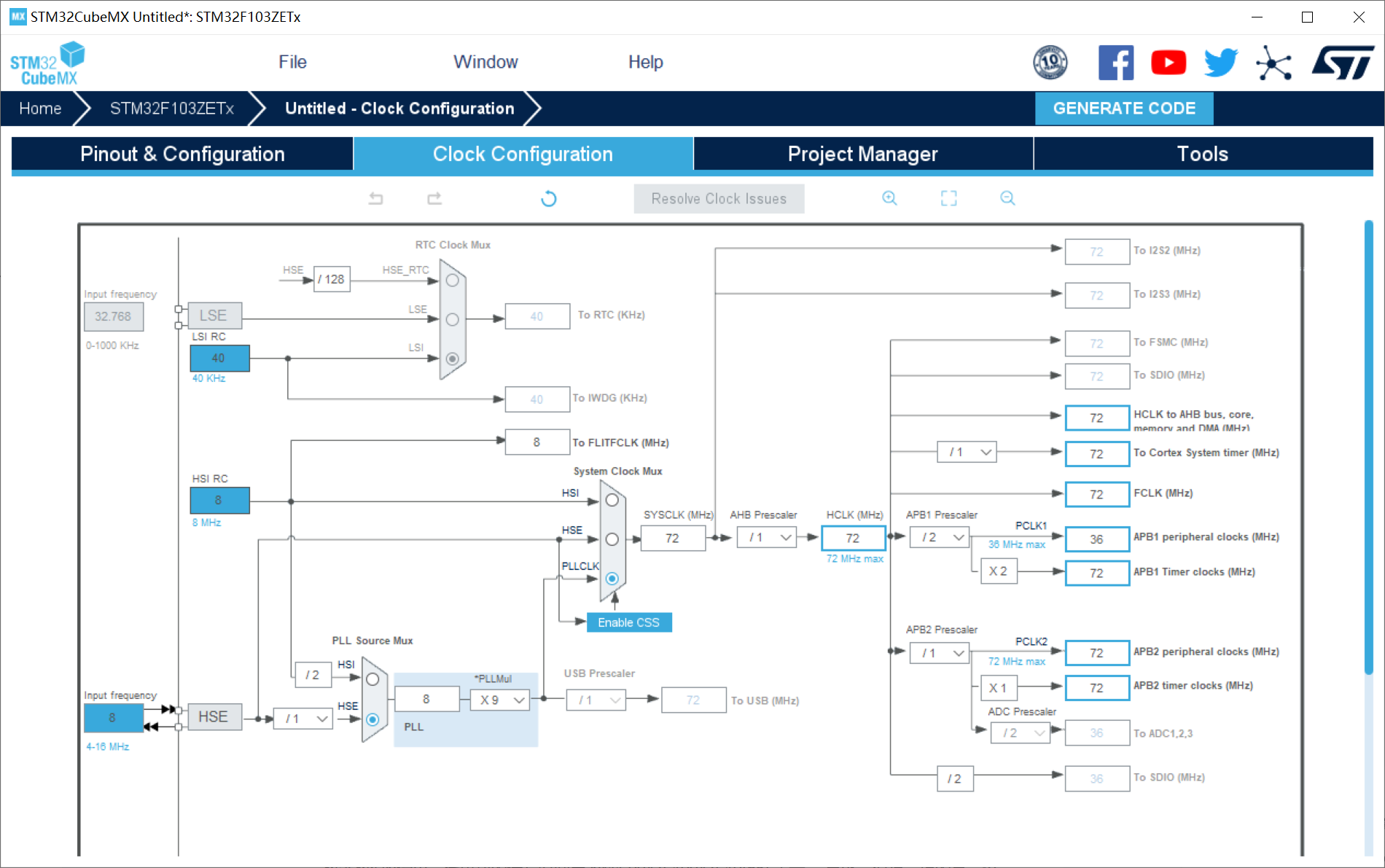
为实现<获取代码块运行时间>的功能，定时器的频率越高，那获取的时间就越精确。因此我们不分频，TIM2 挂在 APB1 上，因此这样配置TIM2的时钟频率是 72MHz。也就是说，定时器每计一个数，代表过去时间 1/72Mhz s，即 13.8888888888889 ns。本例中TIM2的计数周期设为最大，即 (2^16)-1。即，每过 (2^16) * (1/72Mhz) s ≈ 0.00091s，才会触发定时器计数溢出的中断。通常我们认为需测试的代码块运行时间是us级的，是肯定不会超过 0.00091s 的（读者可以自己改为 2^32 来增加上限）。因此实现<获取代码块运行时间>的功能，是需要在代码块运行开始前，将TIM2的计数器设置为0。在代码块运行结束时，把 TIM2 的计数器数值 N 读出。代码块的运行时间用 N*13.8888888888889(ns) 表示。另外，值得一提的是，这个定时器，只有在使用时才会工作，测试运行时间完毕后，可以关闭，定时器各类中断也完没有必要开启。即，仅使用占用少量的CPU资源，不使用时，完全不会占用CPU资源。

4、USART1 配置：利用串口 1 打印出代码块消耗的时间；

5、工程配置：

2.3 代码

这段代码的核心是利用 TIM2 的每次触发时间（作者的 TIM2 每次触发周期时间为 13.8888888888889 ns），通过计算代码块开始与结束时候的 TIM2 触发次数 TIM->CNT 与 TIM2 的触发时间来得到代码块所需消耗的时间。

runtime.h

/********************************* (C) COPYRIGHT **********************************
* File Name						: runtime.h
* Author						: 混分巨兽龙某某
* Version						: V1.0.0
* Data							: 2024/04/12
* Contact						: QQ:1178305328
* Description					: A function that calculates the running time of a block of code
***********************************************************************************/
#ifndef __USERPROGRAM_RUNTIME_H
#define __USERPROGRAM_RUNTIME_Hextern float runtime;void runtime_start(void);
void runtime_stop(void);#endif

runtime.c

/********************************* (C) COPYRIGHT **********************************
* File Name						: runtime.c
* Author						: 混分巨兽龙某某
* Version						: V1.0.0
* Data							: 2024/04/12
* Contact						: QQ:1178305328
* Description					: A function that calculates the running time of a block of code
***********************************************************************************/
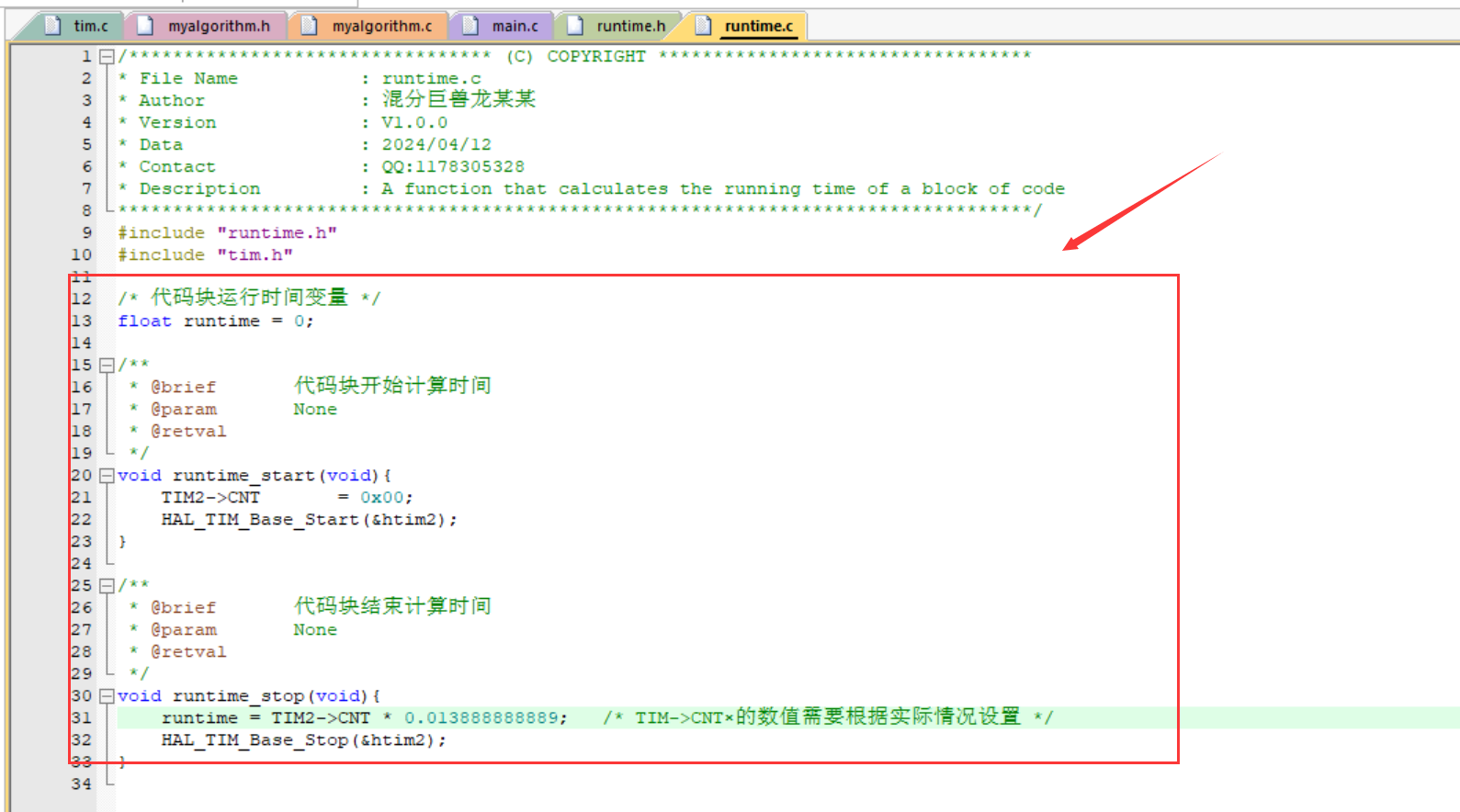
#include "runtime.h"
#include "tim.h"/* 代码块运行时间变量 */
float runtime = 0;/*** @brief       代码块开始计算时间* @param       None* @retval      */
void runtime_start(void){TIM2->CNT       = 0x00;HAL_TIM_Base_Start(&htim2);
}/*** @brief       代码块结束计算时间* @param       None* @retval      */
void runtime_stop(void){    runtime = TIM2->CNT * 0.013888888889;		/* TIM->CNT×的数值需要根据实际情况设置 */HAL_TIM_Base_Stop(&htim2);
}

2.4 代码块耗时实例

三、优化三角函数算法

3.1 sin函数优化

本篇博客利用泰勒级数展开来进行 sin() 函数的优化！！！

勒级数是一种数学上用无限多项的序列来表示函数的方法，这里使用的是正弦函数在0点附近的泰勒展开。

sin() 函数的泰勒级数展开是：

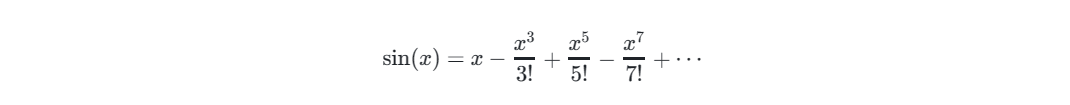
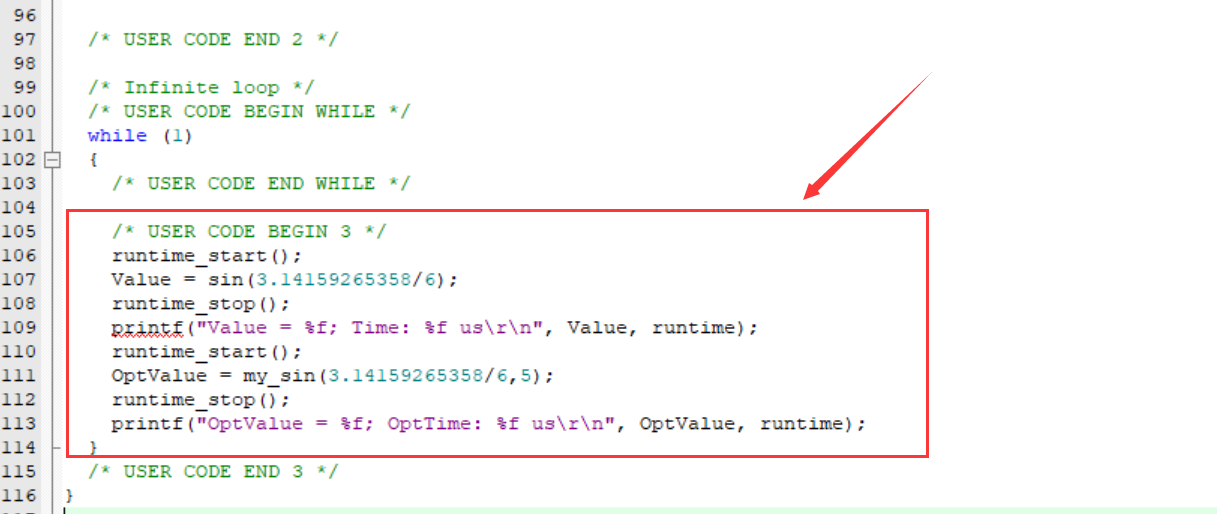
sin_code：

/*** @brief       利用泰勒级数计算sin(x)的近似值* @param       x: 计算的弧度* @param       n: 泰勒级数的项数* @retval      sin函数数值*/
float my_sin(float x,int n) 
{float term = x; // 第一项是 xfloat sin_x = 0.0; // sin(x)的累加结果for (int i = 1; i <= n; i++) {sin_x += term; // 累加当前项term *= -x * x / ((2 * i) * (2 * i + 1)); // 计算下一项}return sin_x;
}

sin() 函数优化的对比：

算法中的 n 也就是泰勒级数的阶数，该数值将影响 sin（）函数的最终输出精度，但是 n 的数值越大，算法计算消耗的时间也越长！

3.2 cos函数优化

本篇博客利用泰勒级数展开来进行 cos() 函数的优化！！！

勒级数是一种数学上用无限多项的序列来表示函数的方法，这里使用的是余弦函数在0点附近的泰勒展开。

cos() 函数的泰勒级数展开是：

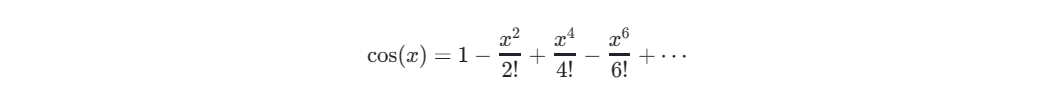
cos_code：

/*** @brief       利用泰勒级数计算cos(x)的近似值* @param       x: 计算的弧度* @param       n: 泰勒级数的项数* @retval      cos函数数值*/
float my_cos(float x,int n) 
{return my_sin(x+M_PI/2,n);//奇变偶不变，符号看象限
}

cos() 函数优化的对比：

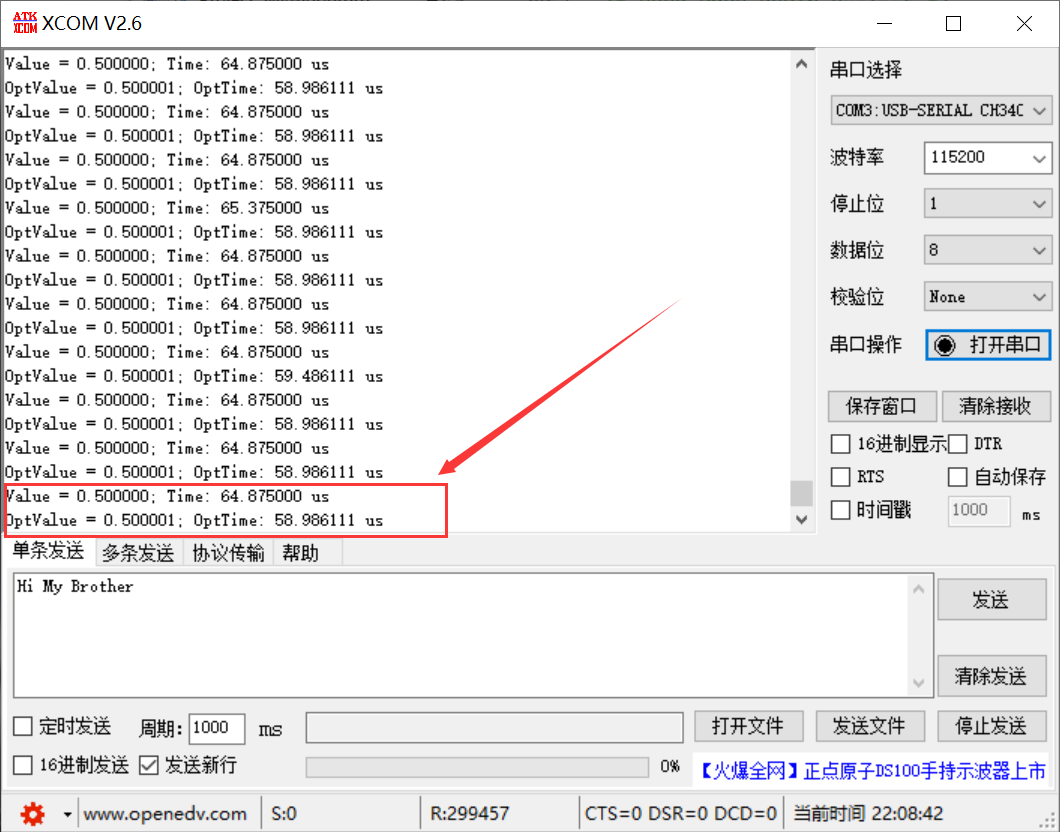
算法中的 n 也就是泰勒级数的阶数，该数值将影响 cos（）函数的最终输出精度，但是 n 的数值越大，算法计算消耗的时间也越长！

3.3 arctan函数优化

反三角函数中的反正切函数（arctan或atan）可以使用麦克劳林级数（Taylor series at 0）来近似计算。反正切函数的麦克劳林级数展开是：

对于接近 0 的 x 值，这个级数是收敛的。

arctan_code：

/*** @brief       利用反正切麦克劳林展开式求解arctan * @param       x: 计算的数值，范围（-1，1）* @retval      arctan函数求解的弧度 * @note        阶数越高，值越准确   70°以内是准确的*/
float arctan(float x)  
{float t = x;float result = 0;float X2 = x * x;unsigned char cnt = 1;do{result += t / ((cnt << 1) - 1);t = -t;t *= X2;cnt++;}while(cnt <= 6); //仅计算前6项return result;
}

arctan函数耗时情况：

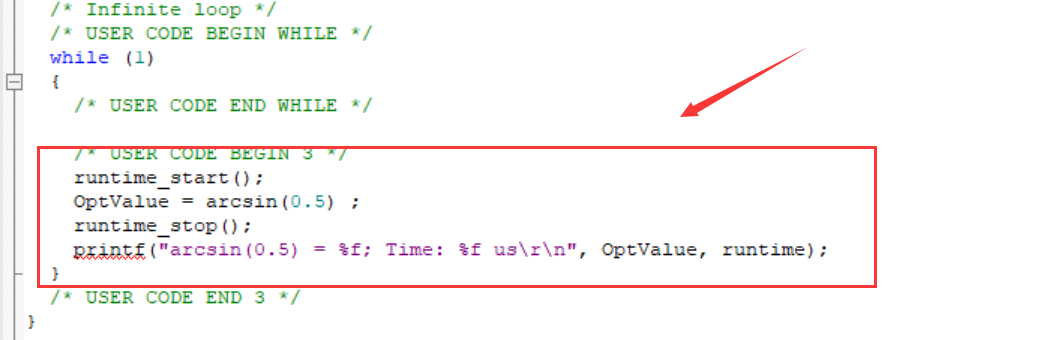
3.4 arcsin函数优化

反正弦函数（arcsin或asin）的麦克劳林级数展开是：

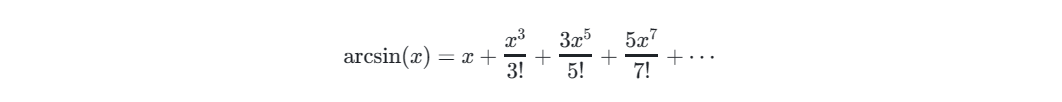
这个级数对于 [-1，1] 之间的 x 值是收敛的。

arcsin_code：

/*** @brief       利用反正切麦克劳林展开式求解arcsin * @param       x: 计算的数值，范围（-1，1）* @retval      arcsin函数求解的弧度 * @note        阶数越高，值越准确   42°以内是准确的*/
float arcsin(float x)  
{float d=1;float t=x;unsigned char cnt = 1;float result = 0;	float X2 = x*x;if (x >= 1.0f) {return PI_2;}if (x <= -1.0f) {return -PI_2;}do{result += t / (d * ((cnt << 1) - 1));t *= X2 * ((cnt << 1) - 1);//d *= (cnt << 1);//2 4 6 8 10 ...cnt++;}while(cnt <= 6);return result;
}

arcsin函数耗时情况：

四、快速开平方根倒数算法

4.1 Q_rsqrt概述

推荐博客地址：http://t.csdnimg.cn/JuyNH

快速开平方根倒数（Fast Inverse Square Root）算法是一种用于计算一个数的平方根倒数的快速方法，它最初在《雷神之锤III竞技场》的源代码中被发现，并因其独特性和效率而广为人知。这个算法的核心思想是利用浮点数的特性来快速近似计算平方根倒数。

算法的核心：利用浮点数的表示方法。在IEEE 754标准中，浮点数由三部分组成：符号位、指数和尾数（或称小数部分）。算法首先将输入的浮点数转换为长整型，然后对这个整型值进行位操作，以得到一个近似的平方根倒数。

该算法的步骤如下：

1. 将浮点数 number 转换为长整型 i。
2. 对 i 进行位操作，得到一个近似的平方根倒数的整数表示。这个操作是通过一个神奇的常数 0x5f3759df 和一个右移操作来完成的。这个常数是经过优化的，它能够产生一个接近于 number 的平方根倒数的近似值。
3. 将得到的整型值转换回浮点数 mongodb。
4. 使用牛顿迭代法（Newton’s method）对 mongodb 进行一次迭代，以提高结果的精度。牛顿迭代法是一种用于求解方程的近似根的方法，它通过迭代的方式来逼近实际的平方根倒数。

最终，算法返回迭代后的结果 y，这个值就是 number 的平方根倒数的近似值。

4.2 代码实现

Q_rsqrt_code：

/*** @brief       快速计算平方根倒数数值* @param       x: 计算的数* @retval      目标数值*/
float Q_rsqrt(float number)
{long i;float x2, y;const float threehalfs = 1.5F;x2 = number * 0.5F;y  = number;i  = * ( long * ) &y;                      i  = 0x5f3759df - ( i >> 1 );               y  = * ( float * ) &i;y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration （第一次牛顿迭代）return y;
}

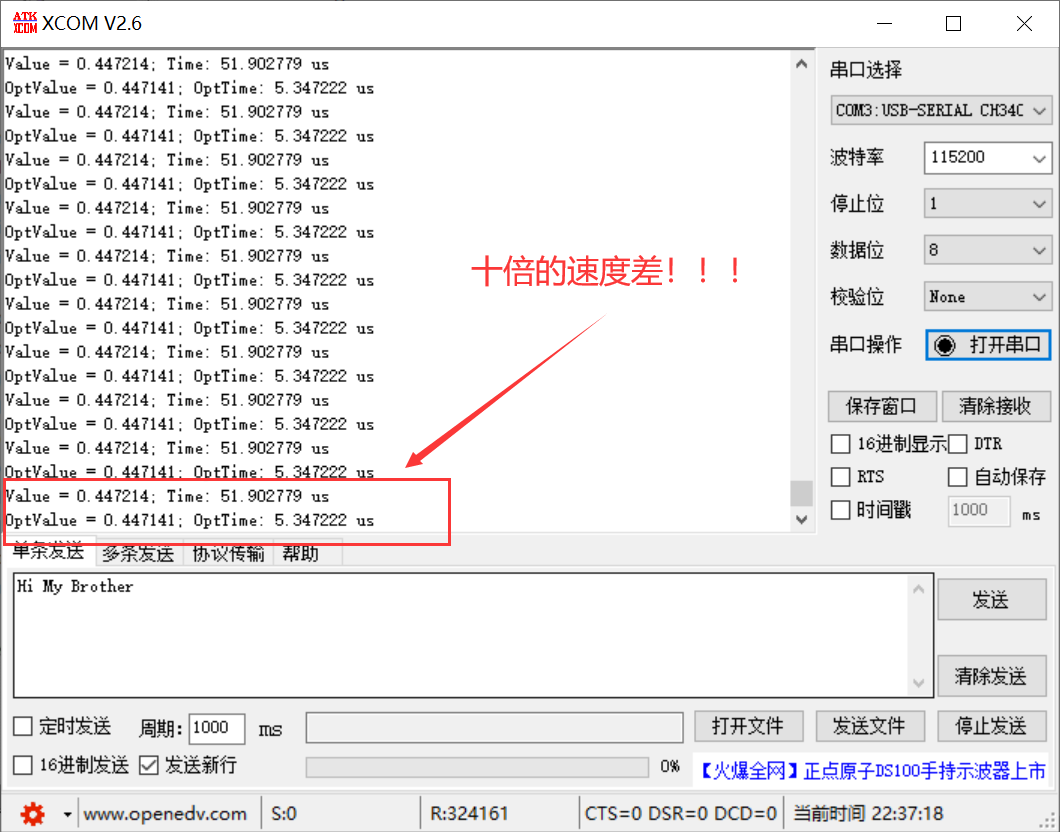
五、优化算法完整代码

myalgorithm.h：

/********************************* (C) COPYRIGHT **********************************
* File Name						: myalgorithm.h
* Author						: 混分巨兽龙某某
* Version						: V1.0.0
* Data							: 2024/04/12
* Contact						: QQ:1178305328
* Description					: This blog compiled optimization algorithm code
***********************************************************************************/
#ifndef __MYALGORITHM_H
#define __MYALGORITHM_H/* 优化三角函数 */
float my_sin(float x, int n);
float my_cos(float x, int n);
float arctan(float x);
float arcsin(float x);/* 优化快速开平方根倒数 */
float Q_rsqrt(float number);#endif

myalgorithm.c：

/********************************* (C) COPYRIGHT **********************************
* File Name						: myalgorithm.c
* Author						: 混分巨兽龙某某
* Version						: V1.0.0
* Data							: 2024/04/12
* Contact						: QQ:1178305328
* Description					: This blog compiled optimization algorithm code
***********************************************************************************/
#include "myalgorithm.h"
#include "math.h"/* PI变量 */
float M_PI = 3.14159265358;
const float PI_2 = 1.570796f;/*** @brief       利用泰勒级数计算sin(x)的近似值* @param       x: 计算的弧度* @param       n: 泰勒级数的项数* @retval      sin函数数值*/
float my_sin(float x,int n) 
{float term = x; // 第一项是 xfloat sin_x = 0.0; // sin(x)的累加结果for (int i = 1; i <= n; i++) {sin_x += term; // 累加当前项term *= -x * x / ((2 * i) * (2 * i + 1)); // 计算下一项}return sin_x;
}/*** @brief       利用泰勒级数计算cos(x)的近似值* @param       x: 计算的弧度* @param       n: 泰勒级数的项数* @retval      cos函数数值*/
float my_cos(float x,int n) 
{return my_sin(x+M_PI/2,n);//奇变偶不变，符号看象限
}/*** @brief       利用反正切麦克劳林展开式求解arctan * @param       x: 计算的数值，范围（-1，1）* @retval      arctan函数求解的弧度 * @note        阶数越高，值越准确   70°以内是准确的*/
float arctan(float x)  
{float t = x;float result = 0;float X2 = x * x;unsigned char cnt = 1;do{result += t / ((cnt << 1) - 1);t = -t;t *= X2;cnt++;}while(cnt <= 6); //仅计算前6项return result;
}/*** @brief       利用反正切麦克劳林展开式求解arcsin * @param       x: 计算的数值，范围（-1，1）* @retval      arcsin函数求解的弧度 * @note        阶数越高，值越准确   42°以内是准确的*/
float arcsin(float x)  
{float d=1;float t=x;unsigned char cnt = 1;float result = 0;	float X2 = x*x;if (x >= 1.0f) {return PI_2;}if (x <= -1.0f) {return -PI_2;}do{result += t / (d * ((cnt << 1) - 1));t *= X2 * ((cnt << 1) - 1);//d *= (cnt << 1);//2 4 6 8 10 ...cnt++;}while(cnt <= 6);return result;
}/*** @brief       快速计算平方根倒数数值* @param       x: 计算的弧度* @retval      目标数值*/
float Q_rsqrt(float number)
{long i;float x2, y;const float threehalfs = 1.5F;x2 = number * 0.5F;y  = number;i  = * ( long * ) &y;                      i  = 0x5f3759df - ( i >> 1 );               y  = * ( float * ) &i;y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration （第一次牛顿迭代）return y;
}