1.Transformer的问题

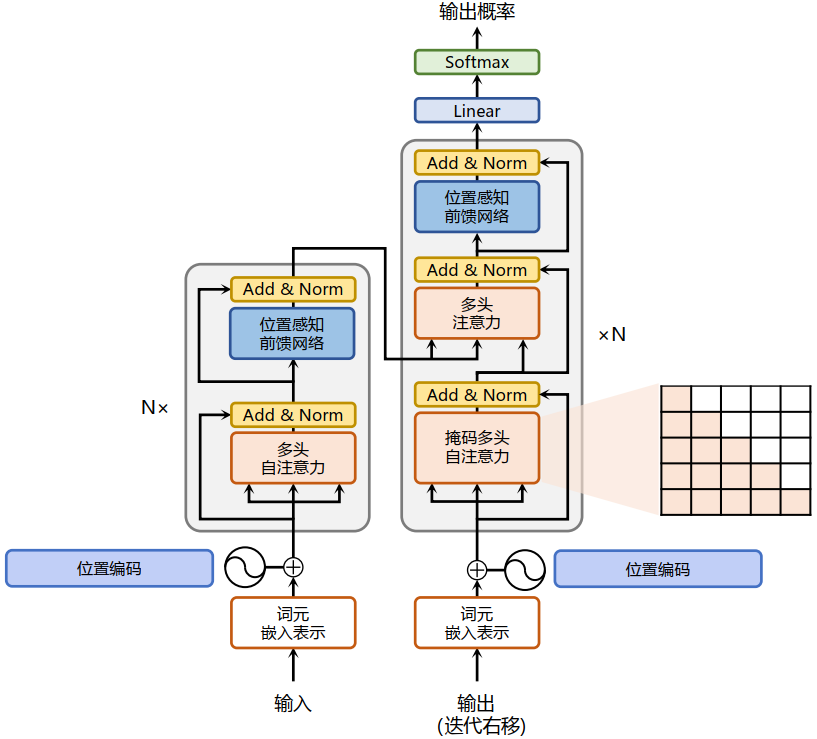
上面是Transformer的网络结构。对于一句话的每个单词，都需要跟所有单词算注意力机制。因此注意力机制的计算复杂度为$O(n^2)$，其中$n$为句子的长度，即单词(符号)的个数。如下图所示。

所以这也是现在大模型如此吃数据和算力、耗电费的根本原因。
然而，这个过程忽视了数据内在结构的关联关系，而是采取一种一视同仁的暴力模式。比如上面的图，整个句子"The animal didn’t cross the street because it was too tired"，很明显，我们把目光注重到"animal"，“street"和"tired"这些名词和形容词就大概了解到整个句子的意思，而对应一些介词"the”，副词"too"其实可以"一眼划过"。

2.State Space Model(线性的时不变系统)

2.1.State Space Model网络结构

SSM(State Space Model)对应公式表述如下：

$h^{\prime }(t)$其实就为下一个$h(t)$的意思，即$h^{\prime }(t)=Ah(t)+Bx(t)$也可以表述为$h_i(t)=A{h}_{i-1}(t)+Bx(t)$。$y(t)$加上$Dx(t)$就类似残差。
我们称之为时不变系统，是因为$ABCD$是不变的，即与$ABCD$时间无关。这是一种假设，而且是一种强假设。

2.2.连续系统离散化

原文State Space Model作者通过"零阶保持(Zero-Order Hold,ZOH)"给出一种从连续系统转换为离散系统的ABC参数对应关系。

对应连续的输入信号后，仅根据固定的输入时间步长$\Delta$对其进行采样。
$\overline{A}=exp(\Delta A),\overline{B}=(\Delta A{)}^{-1}(exp(\Delta A)-I)\cdot \Delta B$

2.3.通过卷积实现SSM并行化

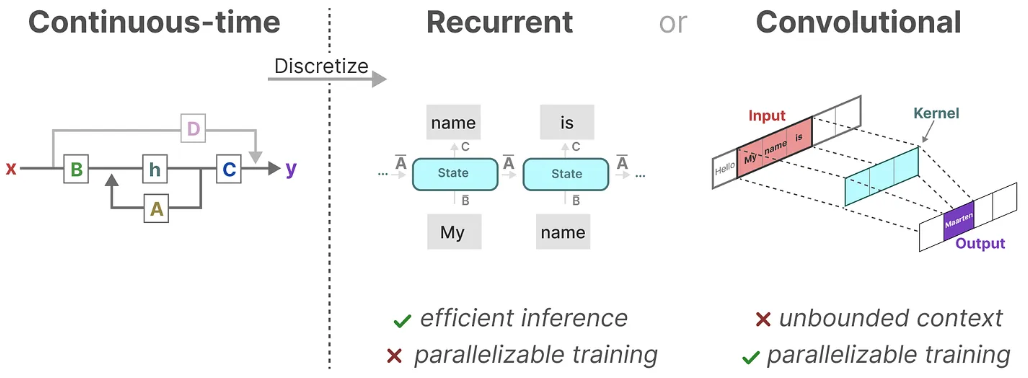
将SSM展开，得到中间图，类似于RNN的感觉。之后，我们可以通过不同的卷积核来模拟同时处理多个输入。

如图所示，通过三种不同的卷积核(图中三种不同颜色的虚线框)进行并行计算，一次输出$y_{k-1},y_k,y_{k+1}$。

3.Mamba——有选择性的SSM

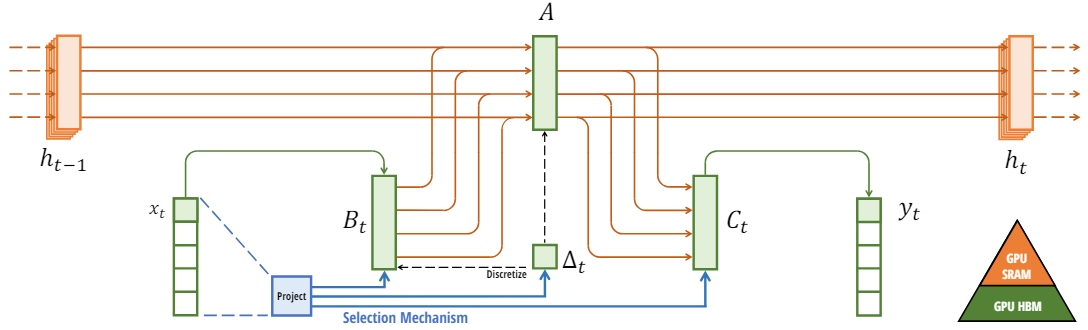
核心思想就是将SSM的时不变性改为时变性，可以看到这里的$B,C$都改成$B_t,C_t$，直接或者间接地受${\Delta }_t$控制，${\Delta }_t$起一个类似总开关的作用。
换句话说，就是让$B$和$C$由固定的变成了可变的，根据输入的$x_t$和它的压缩投影学习可变参数。A为了简化保持不变，蓝色部分（投影及其连线）就是所谓的选择机制。目的是根据输入内容有选择性地记忆和处理信息，从而提高对复杂数据的适应能力。这个思想就类似增加了开关的LSTM。
输入特征维度
对于传统的SSM模型，参数矩阵是静止的。

Mamba对$B,C$进行了调整

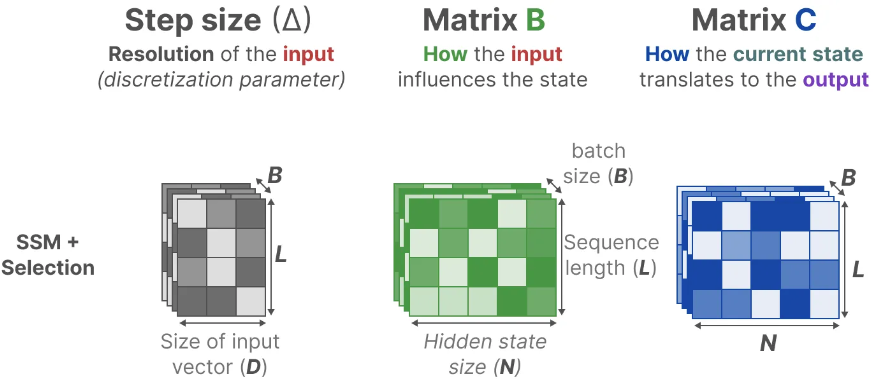
其中步长${\Delta }_t$像是观察窗口。步长较小时，模型倾向于忽略具体的单词，更多地依赖于之前的上下文信息。通过忽大忽小的步长${\Delta }_t$实现注意力机制选择。
注意力机制希望达到的效果

左边是LTI 的效果，输出只能对规则的输入特征进行发现，而右边上面能自己找重点了，带色的尽管开始间隔大小不一，但都能找出来排好队。右下是Mamba希望选择注意力机制达到的能力体现，再看到黑的后就想到以前，后面应该跟着蓝色的。也就是说，对于非线性时变数据，具备了很强的特征捕捉能力。
将大多数SSM架构比如H3的基础块，与现代神经网络比如transformer中普遍存在的门控MLP相结合，组成新的Mamba块。

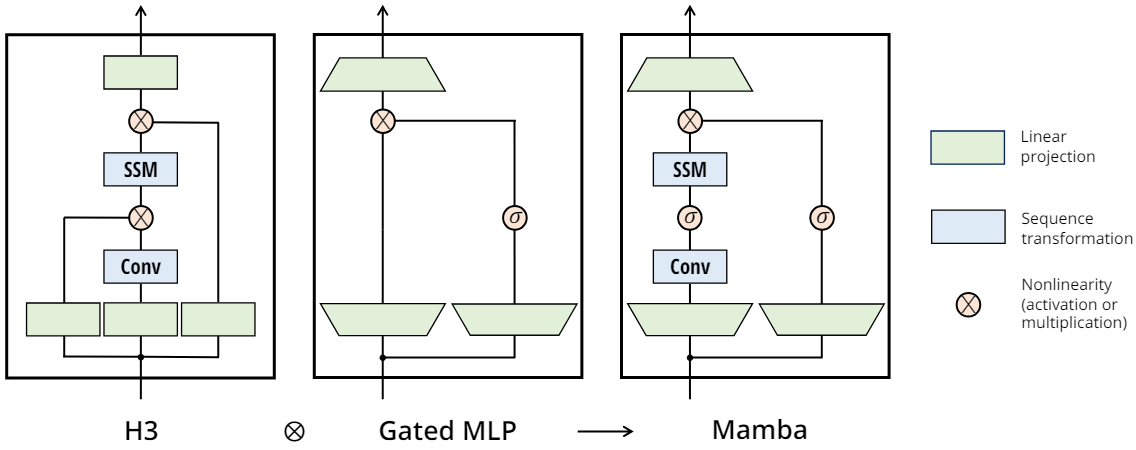
4.从流体力学的角度理解Mamba

本小节从流体力学与李指数映射的角度来理解Mamba，该观点来源于b站up主梗直哥丶(见参考资料1)。
Transformer描述的是粒子运动通过自注意力机制映射动态调整每个输入的权重，牛顿力学互作用力来动态调整自己的动沙似粒子间，通过这训练的过程，就是在用牛顿力学拟合入(粒子)独立计算与其他输入的关系。
而Mamba描述的是流体运动。通过李指数映射来建模时空结构。流体运动描述的是连续介质中的分子集体行为，运动是整体的，内部各点之间有强烈的相互关系和依赖。流体的每个部分都受到整体流体运动的影响，通过内部压力、粘性等因素相互作用。这更符合记忆的本质，因为记忆系统具有连续性、动态变化性和整体关联性，这些特性与流体的性质非常相似。流体模型能够更好地描述记忆中的信息如何相互关联、如何随着时间和新信息的出现进行动态调整和整合。
李指数映射(Lie exponential map)是一种数学工具，用于描述和分析一个向量场如何沿着另一个向量场发生变化，比如流体力学、电磁场、广义相对论的时空结构等，解决了动态系统中相互作用的描述。它是群论和微分几何中重要的概念，来源于李群和李代数的理论，是挪威数学家索菲斯李引入的。
Mamba结构图中，从$h_{t-1}$更新到$h_t$，就类似与人类大脑memory的更新，而是$x_t$就像我们每一次的输入，$y_t$就像我们每一次经过大脑后的输出。
如果把记忆的流淌比作一个水流管道系统，可以看做一个“李群”，进行各种复杂变换(比如旋转、推移等)。固定矩阵 A就是主管道(全局演变路径)，类似于流体运动的全局关系，让系统状态更新有固定的全局路径和规则，因此能表现出更高的灵活性和适应性。$B_t,C_t$就是阀门或旋钮，${\Delta }_t$这个离散化因子，就像是流体力学中的时间步长，决应扩休运动的离散时间点。选择机制就像是根据具体情况选择和调整旋钮，控制流体在管道中的流动路径。
训练 mamba 的过程就是用李指数映射拟合流体力学动态系统，找到主管道$A$，调整阀门和旋钮$B_t,C_t,{\Delta }_t$，获得最优流体流动路径，让模型能在高维特征空间中进行高效导航和决策。
总的来说，跟Transformer的自注意力机制相比，Transformer的自注意力机制更强调个体的独立性，能够捕捉长长距离的上下文依赖关系。而Mamba更强调整体性与全局关系，利用李指数映射实现状态更新与决策。因此，有人认为Mamba在NLP领域是不可能成功的。在NLP领域里边的这种文本的建模非常重要的一点就是长距离依赖的一个建模。Mamba在超过1000token一的这个长度下，它的建模就做不好了。而大模型最有珍贵价值的一点就在于它的这样的一个长距离的一个建模。但是Mamba在CV领域是有很大用处的。Mamba在这个stable diffusion上就是会有很大的用，因为stable diffusion上面的这个我们尤其是在做这个video建模的时候，我们在做这个视频建模的时候，我们可能非常需要建模的就是帧和帧之间的这个连贯性。

参考资料

1.AI大讲堂：革了Transformer的小命？专业拆解【Mamba模型】_哔哩哔哩_bilibili
2.一文通透想颠覆Transformer的Mamba：从SSM、HiPPO、S4到Mamba_mamba模型-CSDN博客
3.《大规模语言模型从理论到实践》张奇 桂韬 郑锐 ⻩萱菁 著
4.Mamba: Linear-Time Sequence Modeling with Selective State Spaces，https://arxiv.org/pdf/2312.00752