文章目录
- 一、说明
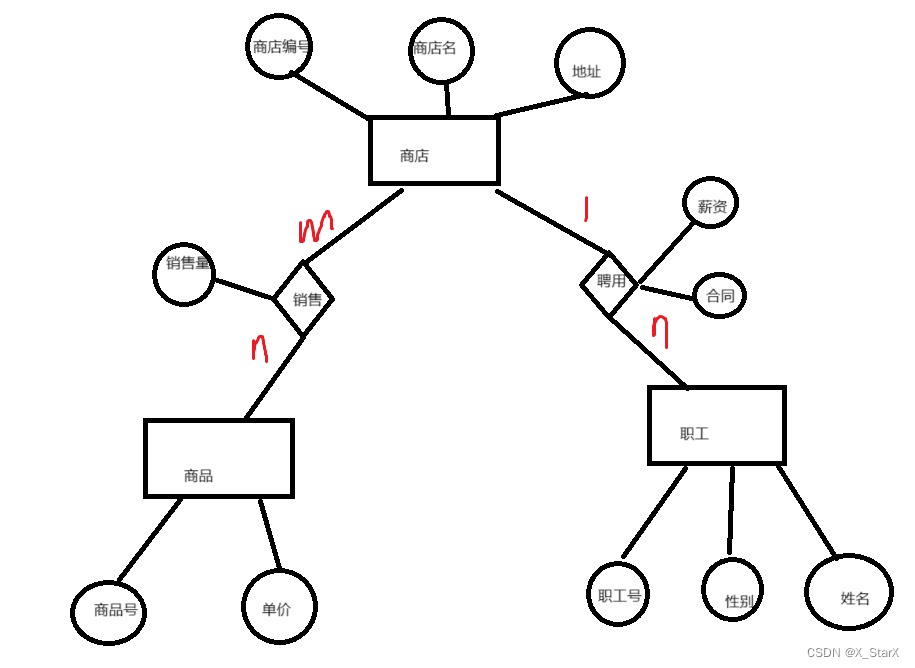
- 二、玩具HMM:5′拼接位点识别
- 三、那么,隐藏了什么?
- 四、查找最佳状态路径
- 五、超越最佳得分对齐
- 六、制作更逼真的模型
- 七、收获
关键词:hidden markov model
一、说明
被称为隐马尔可夫模型的统计模型是计算生物学中反复出现的主题。什么是隐马尔可夫模型,为什么它们对这么多不同的问题如此有用?
通常,生物序列分析只是在每个残留物上贴上正确的标签。在基因鉴定中,我们希望将核苷酸标记为外显子、内含子或基因间序列。在序列比对中,我们希望将查询序列中的残基与目标数据库序列中的同源残基相关联。我们总是可以为任何给定的问题编写一个临时程序,但同样令人沮丧的问题总是会反复出现。一是我们希望整合异构的信息来源。例如,基因发现者应该将剪接位点共识、密码子偏差、外显子/内含子长度偏好和开放阅读框分析结合到一个评分系统中。这些参数应该如何设置?应该如何对不同类型的信息进行加权?第二个问题是从概率上解释结果。找到最佳得分答案是一回事,但分数意味着什么,我们对最佳得分答案是否正确的信心有多大?第三个问题是可扩展性。当我们完善我们的临时基因发现器时,我们希望我们也模拟了翻译起始共识、选择性剪接和多聚腺苷酸化信号。很多时候,将更多的现实堆积在一个脆弱的临时程序上,会使它在自身的重量下崩溃。
隐马尔可夫模型 (HMM) 是建立线性序列“标记”问题的概率模型的形式基础1,2.它们提供了一个概念工具包,只需绘制直观的图片即可构建复杂的模型。它们是各种项目的核心,包括基因查找、图谱搜索、多序列比对和调控位点鉴定。HMM 是计算序列分析的乐高积木。
二、玩具HMM:5′拼接位点识别
举个简单的例子,想象一下下面一个 5’ 剪接位点识别问题的漫画。假设我们得到一个 DNA 序列,该序列从外显子exon开始,包含一个 5’ 剪接位点,以内含子intron结束。问题在于确定从外显子到内含子的转换发生在哪里——5′剪接位点(5′SS)在哪里。
为了让我们智能地猜测,外显子、剪接位点和内含子的序列必须具有不同的统计特性。让我们想象一些简单的差异:假设外显子平均具有均匀的碱基组成(每个碱基 25%),内含子富含 A/T(例如,A/T 各 40%,C/G 各 10%),5′SS 共有核苷酸几乎总是 G(例如,95% G 和 5% A)。
从这些信息开始,我们可以绘制一个 HMM(图 1)。HMM 调用三种状态,一种状态对应我们可能分配给核苷酸的三个标签:E(exon)、5(5′SS)和 I(intron)。每个状态都有自己的发射概率(如上所示),它模拟了 5′SS 处外显子、内含子和共识 G 的基本组成。每个状态也有转换概率(箭头),即从这个状态移动到新状态的概率。转移概率描述了我们期望状态发生的线性顺序:一个或多个 E、一个 5、一个或多个 I。
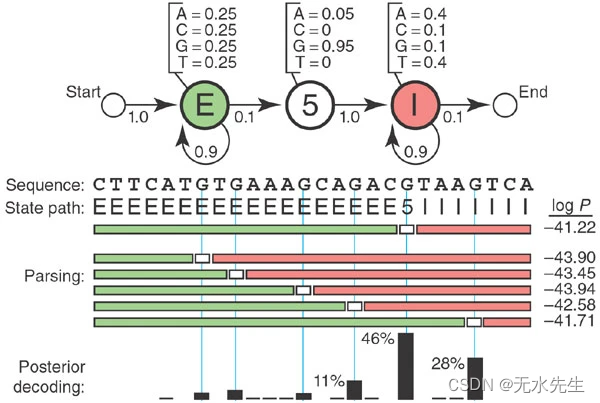
图 1:用于 5’ 剪接位点识别的玩具 HMM。
三、那么,隐藏了什么?
想象一个 HMM 生成一个序列是很有用的。当我们访问一个州时,我们会从该州的排放概率分布中排放出残留物。然后,我们根据该州的转移概率分布选择接下来要访问的州。因此,该模型生成了两串信息。一个是基础状态路径(标签),当我们从一个状态转换到另一个状态时。另一个是观察到的序列(DNA),每个残基都从状态路径中的一个状态发射出来。
状态路径是马尔可夫链,这意味着我们接下来要进入的状态仅取决于我们所处的状态。由于我们只得到了观察到的序列,所以这个底层状态路径是隐藏的——这些是我们想要推断的残基标签。状态路径是一条隐藏的马尔可夫链。
概率 P(S,π|HMM,θ),具有参数 θ 的 HMM 生成状态路径 π,观测到的序列 S 是所使用的所有发射概率和跃迁概率的乘积。例如,考虑图 1 中间的 26 个核苷酸序列和状态路径,其中有 27 个跃迁和 26 个发射需要处理。将所有 53 个概率相乘(并取对数,因为这些数字很小),您将计算对数 P(S,π|HMM,θ) = −41.22。
HMM 是一个完全概率模型——模型参数和整体序列“分数”都是概率。因此,我们可以使用贝叶斯概率论以标准、强大的方式操纵这些数字,包括优化参数和解释分数的重要性。
四、查找最佳状态路径
在分析问题中,我们得到了一个序列,我们想要推断隐藏的状态路径。可能有许多状态路径可以生成相同的序列。我们想找到概率最高的那个。
例如,如果我们在图 1 中给定 HMM 和 26 个核苷酸序列,则有 14 条可能的路径具有非零概率,因为 5′SS 必须落在 14 个内部 As 或 G 之一上。最好的一个的对数概率为 −41.22,这推断出最有可能的 5′SS 位置位于第五个 G。
对于大多数问题,有太多可能的状态序列,我们无法枚举它们。高效的 Viterbi 算法保证在给定序列和 HMM 的情况下找到最可能的状态路径。维特比算法是一种动态规划算法,与用于标准序列比对的算法非常相似。
五、超越最佳得分对齐
图 1 显示,一个替代状态路径与将 5′SS 置于第五个 G 的分数略有不同(对数概率为 -41.71 对 -41.22)。我们对第五个G是正确的选择有多大信心?
这是概率建模优势的一个例子:我们可以直接计算我们的置信度。状态 k 发出残基 i 的概率是使用状态 k 生成残基 i(即 π我 = k 在状态路径 π) 中,由所有可能的状态路径的总和归一化。在我们的玩具模型中,这只是分子中的一条状态路径和分母中 14 条状态路径的总和。我们得到得分最高的第五个 G 正确率为 46%,第六个 G 位置正确率为 28%(图 1,底部)。这称为后验解码。对于较大的问题,后验解码使用两种称为“前向”和“后向”的动态规划算法,它们本质上类似于 Viterbi,但它们对可能的路径求和,而不是选择最佳路径。
六、制作更逼真的模型
制作 HMM 意味着指定四件事:(i) 符号字母表,K 个不同的符号(例如,ACGT,K = 4); (ii)模型中的状态数,M;(iii) 排放概率 e我(x) 对于每个状态 i,该总和 1 超过 K 符号 x, Σxe我(x) = 1;(iv)转移概率t我(j) 对于每个状态 i 到任何其他状态 j(包括它自己),其总和为 1 超过 M 状态 j, Σjt我(j) = 1。任何具有这些属性的模型都是 HMM。
这意味着只需绘制与手头问题相对应的图片即可制作新的 HMM,如图 1 所示。这种图形的简单性使人们可以清楚地关注问题的生物学定义。
例如,在我们的玩具拼接站点模型中,也许我们对自己的辨别能力不满意;也许我们想在 5’ 剪接位点添加一个更现实的六核苷酸共识 GTRAGT。我们可以用一行六个 HMM 状态代替“5”状态,以模拟一个六碱基无固定的共识基序,参数化已知 5’ 剪接位点的发射概率。也许我们想模拟一个完整的内含子,包括一个 3’ 剪接位点;我们只需为 3′SS 共识添加一行状态,并添加一个 3′ 外显子状态,让观察到的序列以外显子而不是内含子结束。那么也许我们想建立一个完整的基因模型…无论我们添加什么,都只是画出我们想要的东西。
七、收获
HMM 不能很好地处理残基之间的相关性,因为它们假设每个残基仅取决于一种基础状态。HMM 通常不合适的一个例子是 RNA 二级结构分析。保守的RNA碱基对诱导长程成对相关性;一个位置可能是任何残基,但碱基配对的伴侣必须是互补的。HMM 状态路径无法“记住”遥远状态生成的内容。
有时,人们可以在不破坏算法的情况下弯曲 HMM 的规则。例如,在基因发现中,人们想要发射一个相关的三重密码子,而不是三个独立的残基;HMM 算法可以很容易地扩展到三重态发射态。但是,基本的 HMM 工具包只能延伸到此为止。除了HMM之外,还有更强大(尽管效率较低)的概率模型用于序列分析。






![[vue2]深入理解路由](https://img-blog.csdnimg.cn/img_convert/552275e60449aceaeb7c47442dc61c93.png)