一、定义

          基于核方法的线性回归模型和传统线性回归一样，可以用未知数据进行预测，但不能确定

预测的可信度。在参考书第二章中可知，基于贝叶斯方法可以实现对未知数据依概率预测，进而可得到预测的可信度。这一方法中，通过对模型参数w引入先验概率p(w),通过学习可得到该参数的后验概率p(w|D),并以此对x进行依概率预测，形式化如下：

        1---(1)

          其中 是生成模型，可以是任何已知或设定的某种分布形式的模型，每个模型由w唯一确定，p(w|D)是基于训练数据D得到的对w的后验估计，计算如下：

  1---(2)

         上式通过w的先验概率p(w)来实现对每个具体模型赋予先验概率。在核方法中，由于不存在一个显式的w,因此通过引入先验的方法无法适用。从而这里引入了高斯过程回归，而高斯过程回归就是基于核方法并引入随机性为高斯分布的一种统计回归方法，回归的结果就是高斯随机预测函数，并且可以得到预测的信度。

  二、高斯过程回归的推导

      2.1 高斯过程

          高斯过程是随机过程的一种。随机过程和随机变量相对，是反映一系列变量或一组变量的分布特性，即各个组成变量以某种随机规律或分布取值。假设集合Ｘ有x1、x2.....xｎ个变量，如对每个变量进行一次采样，这些采样值就构成了一个定义在Ｘ上的函数f,这一函数显然是随机函数，而且f的形式显然就定义了具体的随机过程，所以也可以认为随机过程是以随机函数为自变量的概率分布，这个”概率分布“由f变量随机生成采样值生成。

　　   任何一个变量集合Ｘ（进行采样）所蕴含的有限维函数分布族满足一致性和对称性就能保证Ｘ为一随机过程，且这一有限维函数分布族恰好就是该随机过程的有限维分布函数。这称之为      Kolmogorov定理。

　　    所谓一致性就是，是指从Ｘ中任选一个子集，得到的概率分布形式是一致的。更严格地说，如果存在两个子集Ｘ1和Ｘ２，且,则由Ｘ１或Ｘ２通过边缘化其他变量导出的应一致，即：

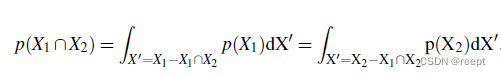
　　1---(3)

      对称性，是指Ｘ中任选一个子集，当对子集的变量交换位置时，其分布函数不变。

Kolmogorov定理表明，集合Ｘ确定的随机过程可以由其任意自己的子集的分布形式描述（Finite-Dimensional Distribution,f.f.d）

2.2 高斯过程回归推导

    　高斯过程是f.f.d为高斯分布的一种随机过程，即任取一个有限点集组成的矩阵Ｘ＝[x1,x2,...xn],其目标变量取值组成的向量y=[y1,y2,...yn]满足高斯分布Ｎ(y;(X),K(x) )。设

(X) =0，则该高斯过程由协方差矩阵K(x)确定，其中K(X)ij = k(xi,xj), k(.,.)为任意核函数。

     已知一个集合的分布形式，则任意一个子集也具有同样的分布，这一性质可以用来采样一个高斯过程，假设当前已经完成采样的函数点集为X，对一个新采样点 ,有 =  对应的采样值同样符合高斯分布。

   即：1----(4)

其中：

  1---(5)

其中，K是训练集X的Gram矩阵， =k(,), v = k()。由高斯分布的性质，可知其条件分布也是高斯的，即：

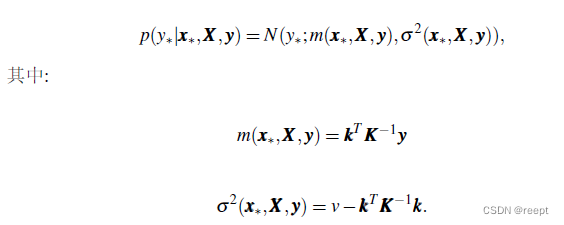1--(6)  1---(7) 1---(8)

      下面用高斯过程完成回归任务，设有训练集{},定义如下回归模型：

                 1---(9)

其中y是一个高斯过程，是观测噪音，则有：

  1---（10）

由于p(t|y)和p(y)都是高斯的，有积分p(t)：

p(t) = N(t;0,C)   1---（11）

其中：C= K +  1----（12）

1-----（11）式实际上就完成了一次高斯回归。

因此 t 也是一个高斯过程，基于式类似1---（6）的推导过程，可知对于增量,可得类似的条件高斯回归模型，进而得到回归结果：

   

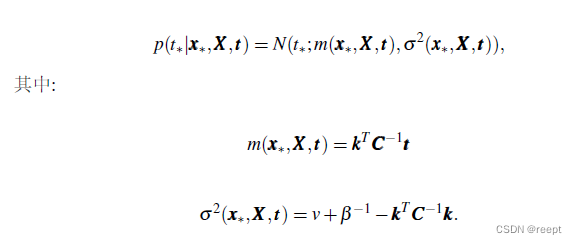
 1----（13）、1----（14）、1----（15）

    回顾上述推导过程，可以发现并没有定义一个类似线性回归的显示预测函数，而是通过定义数据间的相关性来描述整体分布属性，从而隐式定义了从x-->y的随机预测函数y(x),即高斯过程。

     和参考书5.1节中基于核方法的正则化线性回归模型相比，高斯过程不仅引入了数据间的距离，而且通过该距离定义了一个联合概率分布，从而引入了预测模型的随机性。

    引入这一随机性事实上给出了预测过程的可信度。比较参考书5.9式: 

和 1---（14）可知 基于高斯过程预测的期望值和传统核方法得到的预测值是一致的（ 和  形式一致）。但高斯分布给出了1---（15）式的估计方差。

因此高斯过程回归可以认为是传统核方法的随机版本。

三、总结

           本文是学习《机器学习导论》（清华大学出版社，中文版，王东，2021年）的摘录总结或笔记。