把夜熬成粥，然后喝了它。

——2024年7月1日

---

书接上回：区间动态规划——最长回文子串（C++）-CSDN博客，大家有想到解决办法吗？

题目描述

        给定一个字符串s（s仅由数字和英文大小写字母组成，长度为1~1000），求s中最长的回文子序列长度。例如，s = “aferegga”，最长的回文子序列为“aerea”，其长度为5。

---

题解思路

        区间动态规划

下面是个人的思路：

1. 定义dp数组

        定义 dp[i][j]表示 s[i...j] 中最长回文子序列长度。

2. 确定dp限制条件

注：len表示字符串长度

        ①对于任何 len == 1 的字符串，dp[i][j] = 1；

        ②对于任何 len == 2 的字符串，dp[i][j] = dp[i][j-1] + (s[i] == s[j])；

        ③对于任何 len  ≥  3 的字符串，有两种情况：

        如果 s[i] == s[j]，那么dp[i][j] = dp[i+1][j-1] + 2；

        如果 s[i] != s[j]，那么dp[i][j] = max(dp[i+1][j]，dp[i][j-1])；

解释如下：

        第一种情况，如果字符串长度为1的话，那么它一定是回文子串，长度唯一；

        第二种情况，如果字符串长度为2，那它就有两种可能，要么这两个字符相等，要么不等，不管哪一种情况，这个字符串的回文子序列至少是大于等于1的（第一种情况），如果相等，无非是把这个相等的加上即可。

        第三种情况，字符串长度不小于3时，也有两种可能：
        如果 s[i] == s[j]，那么当前最长回文子序列长度就等于上一次的回文子序列长度加上2（两个相同的字符），也可以表示为dp[i][j] = dp[i+1][j-1] + 2*(s[i] == s[j])；
        如果 s[i] != s[j]，那么当前最长回文子序列长度至少是在 s[i+1....j]和s[i....j-1]中取最大值，即dp[i][j] = max(dp[i+1][j]，dp[i][j-1])。

---

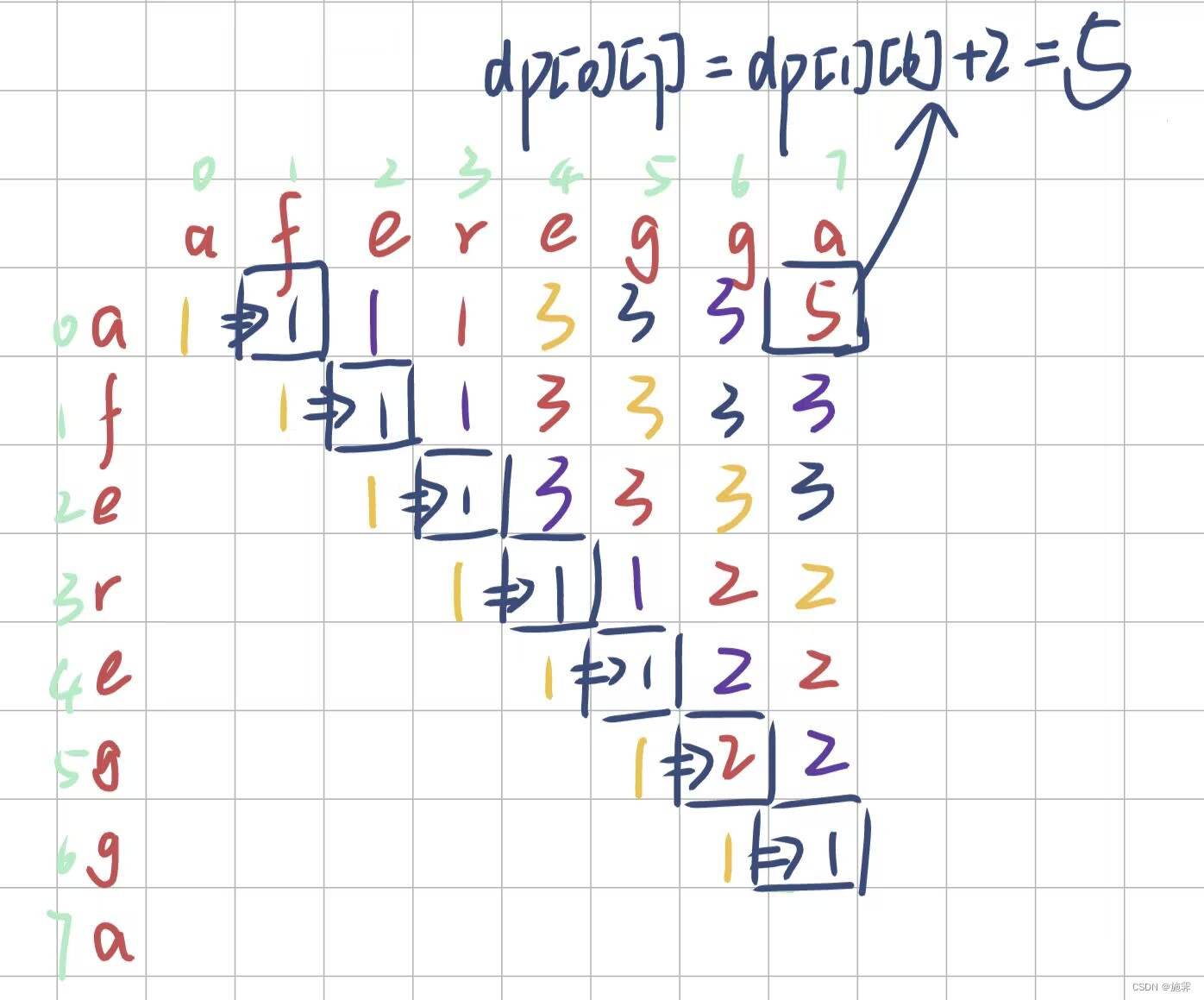
推导过程

用矩阵推导如下：

 

代码展示

// 最长回文子序列长度
int getLongestPalind(string s){int size = s.size();vector<vector<int>> dp(size, vector<int> (size, 0));// 定义dp数组// dp[i][j]表示从i到j的最长子回文字符串长度for(int len = 1; len <= size; len++){for(int i = 0; i + len - 1 < size; i++){int j = i + len - 1;if(len == 1){dp[i][j] = 1;}else if(len == 2){dp[i][j] = dp[i][j-1] + (s[i] == s[j]);}else{if(s[i] == s[j]){dp[i][j] = dp[i+1][j-1] + 2 * (s[i] == s[j]);}else{dp[i][j] = max(dp[i+1][j], dp[i][j-1]);}}}}return dp[0][size-1];
}

运行结果

完整代码

// 区间动态规划
#include<iostream>
#include<vector>
#include<string>using namespace std;// 最长回文子序列长度
int getLongestPalind(string s){int size = s.size();vector<vector<int>> dp(size, vector<int> (size, 0));// 定义dp数组// dp[i][j]表示从i到j的最长子回文字符串长度for(int len = 1; len <= size; len++){for(int i = 0; i + len - 1 < size; i++){int j = i + len - 1;if(len == 1){dp[i][j] = 1;}else if(len == 2){dp[i][j] = dp[i][j-1] + (s[i] == s[j]);}else{if(s[i] == s[j]){dp[i][j] = dp[i+1][j-1] + 2 * (s[i] == s[j]);}else{dp[i][j] = max(dp[i+1][j], dp[i][j-1]);}}}}return dp[0][size-1];
}int main(){string s;cout<<"请输入字符串s：";cin>>s;cout<<"最长回文子序列长度为"<<getLongestPalind(s)<<endl;return 0;
}