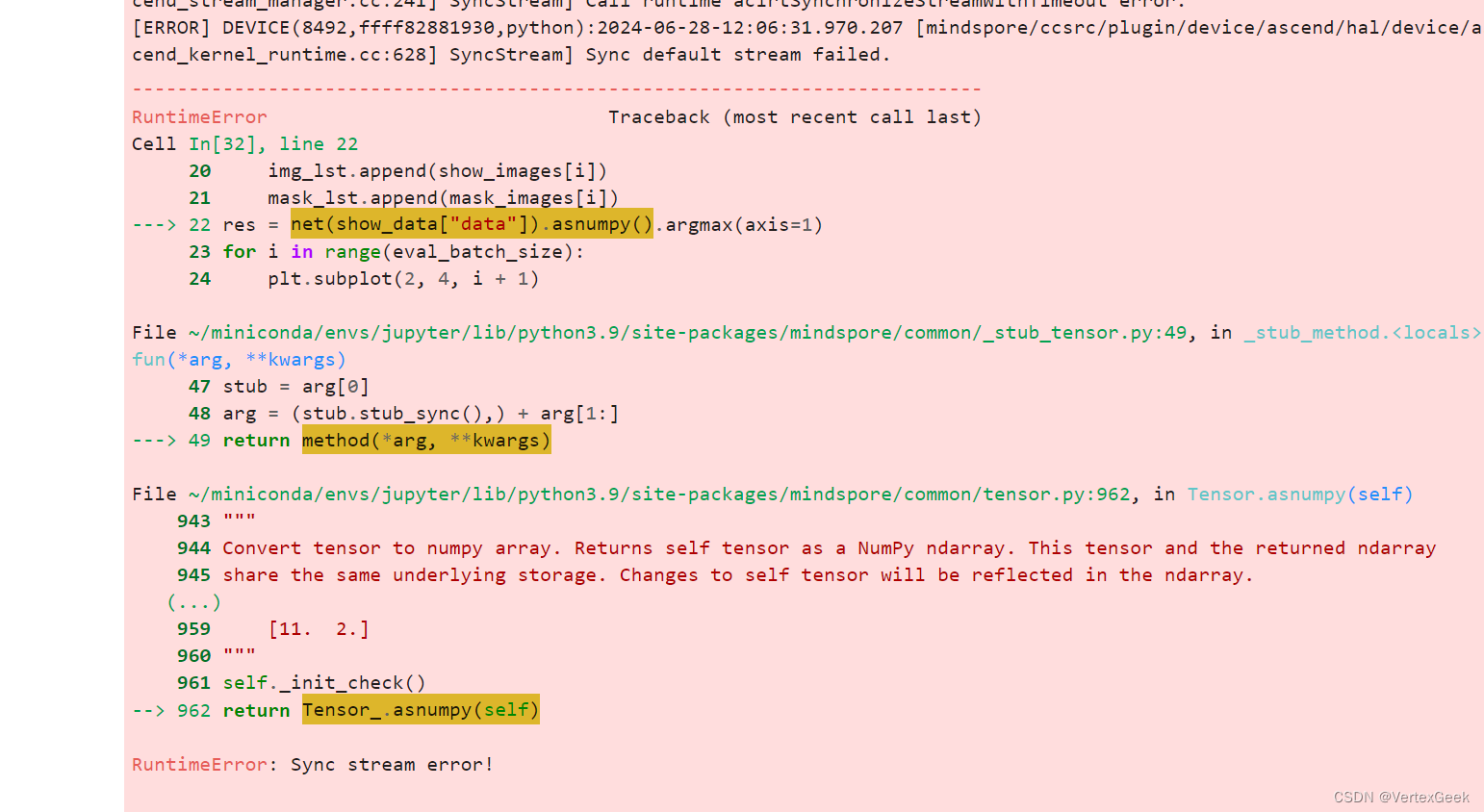
摘要：什么是红黑树，模拟实现红黑树

红黑树 ，是一种 二叉搜索树 ，但 在每个结点上增加一个存储位表示结点的颜色，可以是  Red 或 Black 。 通过对 任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路 径会比其他路径长出俩倍 ，因而是 接近平衡 的。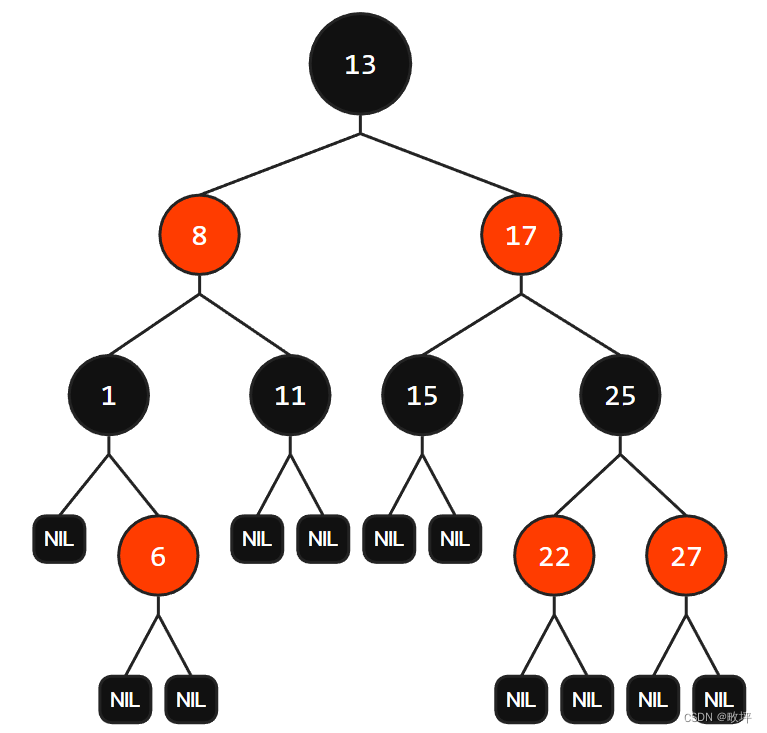

---

1. 红黑树的性质

注意：红黑树是一种搜索二叉树。性质如下：

① 红黑树的根节点为 Black ；

② Red 节点不连续，即 Red 节点一定有 Black 的孩子节点；

③ 每条路径含有相同数量的 Black 节点；（关于这点下文会详细解释）

④ 每个节点要么是 Black 的要么是 Red 的；

⑤ nullptr 节点为 Black。（在红黑树中这样的节点被称为NIL节点，这样是为了方便找准路径，非硬性要求）

• 路径 - path：指从根节点到空，称为一条路径。
  最短路径：如果一条路径的所有节点均为 Black ，则该路径为最短路径；
  最长路径： Black Red Black Red Black Red Black ……Red NIL 这样总是黑红节点相间的路径为最长路径。（注意：路径的结尾为空节点，而空节点一定是 Black 的，又因为红黑树的每条路径含有数量相同的 Black 节点，因此可得最长路径=最短路径×2-1）

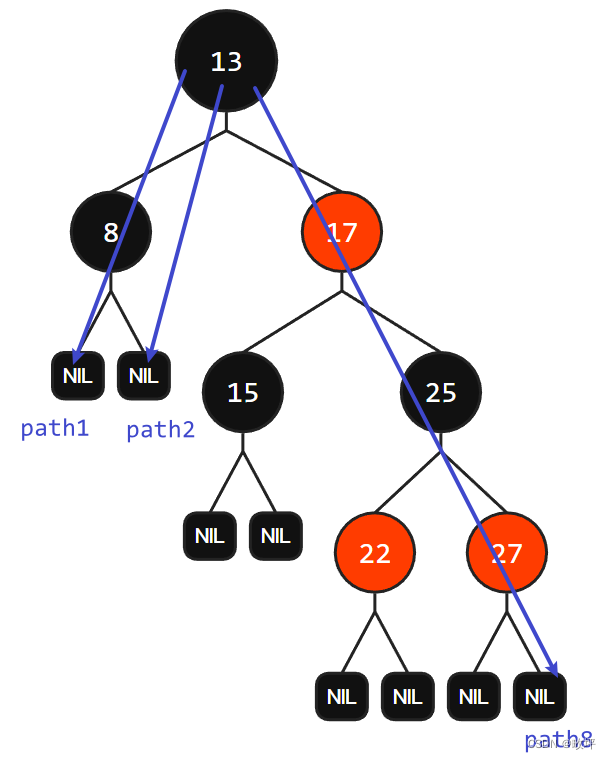如图所示，path1和path2为该红黑树的最短路径；path8为该红黑树的最长路径。红黑树中的叶节点为特殊的叶节点，即 nullptr 节点，在此图中写作“NIL”。
与AVL树比较，AVL树是更接近满二叉树的严格平衡，而红黑树是近似平衡。

---

2. 模拟实现红黑树

1）框架

同样的，先定义红黑树的节点。根据红黑树对节点的“颜色”要求，这里采用枚举(enum)类型来表达节点的“颜色”。示例代码如下。

ps.默认新创建的节点为红色（下文会解释这样做的原因）。

enum Colour
{RED, BLACK
};template<class T>
struct RBTreeNode
{RBTreeNode(T data = T()):_data(data), _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _col(RED)//默认新创建的节点都是红色的{}T _data;RBTreeNode<T>* _pLeft;RBTreeNode<T>* _pRight;RBTreeNode<T>* _pParent;Colour _col;
};// 模拟实现红黑树的插入--注意：为了后序封装map和set，在实现时给红黑树多增加了一个头结点
template<class T>
class RBTree
{typedef RBTreeNode<T> Node;
public:RBTree(){_pHead = new Node;_pHead->_pLeft = _pHead;_pHead->_pRight = _pHead;}private:Node* _pHead;
};

2）insert

红黑树的插入函数实现的思路同AVL树是类似的。

-🟡Part1.插入新节点-   红黑树首先是一个BST，先按BST的规则插入新节点。代码如下。注意：当我们插入新的节点时，总是默认新插入的节点为红色。理由是：如果在红黑树中插入黑色节点将对整棵红黑树造成影响，因为红黑树要求每条路径上含有数量相同的黑色节点，一旦插入黑色节点必然要应对红黑树的调整，而插入红色节点，若该新节点的parent节点不为红色节点则不用调整这棵红黑树。

// 在红黑树中插入值为data的节点，插入成功返回true，否则返回false.注意：为了简单起见，本次实现红黑树不存储重复性元素
bool Insert(const T& data)
{if (_pHead->_pLeft == _pHead && _pHead->_pRight == _pHead){Node* _pNewNode = new Node(data);_pHead->_pLeft = _pHead->_pRight = _pNewNode;_pNewNode->_pParent = _pHead;_pNewNode->_col = BLACK;//跟节点为黑色return true;}Node* pCur = _pHead->_pLeft;Node* pParent = pCur->_pParent;while (pCur){pParent = pCur;if (pCur->_data > data){pCur = pCur->_pLeft;}else if (pCur->_data < data){pCur = pCur->_pRight;}else{return false;}}Node* _pNewNode = new Node(data);if (pParent->_data > data)pParent->_pLeft = _pNewNode;elsepParent->_pRight = _pNewNode;_pNewNode->_pParent = pParent;//……return true;
}

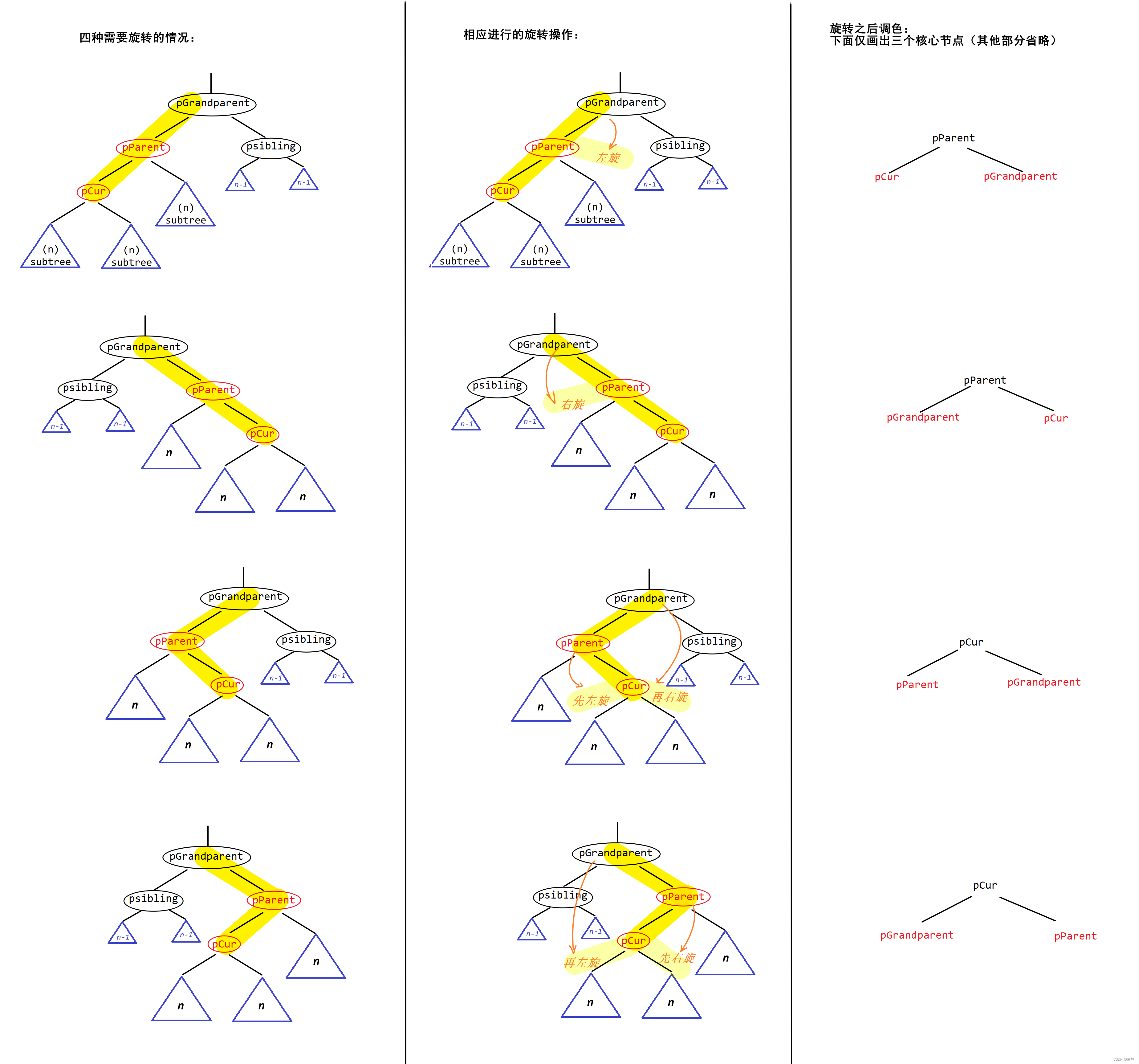
-🟡Part2.调整红黑树-  由于插入的新节点默认为红色，因此当插入导致出现连续的红色节点时，需要调整红黑树。 

如上图。下一步，继续对圈出的subtree进行展开：👇

• 情况一：当圈出的subtree的根节点 psibling 为红色，这种情况不需要旋转，直接调整节点颜色即可。从下图的换色中不难看出，这样换色之后，每个路径的黑色节点数量不受影响。注意：当 pGrandparent 变为红色后，可能会与 其parent 形成连续的红色节点，因此需要继续向上操作，即令 pCur = pGrandparent（赋值操作），继续判断，并在必要的情况下调整。（这个“向上的”思路和AVL树的调整是类似的）
  ps.pParent 不一定是 pGrandparent 的左节点，pCur 不一定就是 pParent 的左节点。这里之所以只分析下图中的这一种情况是因为，这类情况的调整不需要旋转，即直接调整节点颜色——pParent和psibling都变红，因此这两个节点相对于pGrandparent的左右位置不重要，pCur不做改变，因此pCur相对于pParent的左右位置也不重要。但需要旋转调整的情况就不一样了，pParent 、pGrandparent 、pCur 这三个节点之间的关系决定了旋转的方向，下面“情况二”会详细讲解。
  
• 情况二：当圈出的subtree根节点为黑色，这种情况需要旋转+调色，下面对这种情况继续细分。👇
  ps.这棵被圈出的 subtree 黑色节点数目为n，在情况二这种情况下，psibing已经是一个黑色节点了，因此其子树黑色节点为n-1，如图中所写。(n≥1) 另外，注意 psibing 可能为NIL，即黑色的空节点。
  
  如下图，第三列表示调色后的结果，调色思路可以归纳为——旋转后的树的新根变为黑色，旋转前的树的旧根变为红色。

示例代码：

{//RBTree// 在红黑树中插入值为data的节点，插入成功返回true，否则返回false.注意：为了简单起见，本次实现红黑树不存储重复性元素bool Insert(const T& data){//前面插入新节点的部分省略///新插入的节点默认是红色的，因此若在这条含有新插入节点的路径中出现·连·续·红·色·节点则需要调整///pCur = _pNewNode;//以新插入的结点为起点向上调整while (pCur->_col == RED && pParent->_col == RED){Node* pGrandparent = pParent->_pParent;Node* pP_sibling = pGrandparent->_pLeft == pParent ? pGrandparent->_pRight : pGrandparent->_pLeft;if (pP_sibling && pP_sibling->_col == RED)//调色{pParent->_col = pP_sibling->_col = BLACK;if (pGrandparent != _pHead->_pLeft){pGrandparent->_col = RED;pCur = pGrandparent;pParent = pCur->_pParent;}}else//旋转+调色{if (pCur == pParent->_pLeft){if (pParent == pGrandparent->_pLeft)//右旋{RotateR(pGrandparent);pParent->_col = BLACK;}else//右左双旋{RotateR(pParent);RotateL(pGrandparent);//双旋后pCur成为新的subrootpCur->_col = BLACK;}pGrandparent->_col = RED;}else if (pCur == pParent->_pRight){if (pParent == pGrandparent->_pRight)//左旋{RotateL(pGrandparent);//左旋后pParent成为新的subrootpParent->_col = BLACK;}else//左右双旋{RotateL(pParent);RotateR(pGrandparent);pCur->_col = BLACK;}pGrandparent->_col = RED;}}}return true;}private:// 左单旋void RotateL(Node* subroot){Node* pGrandparent = subroot->_pParent;Node* subR = subroot->_pRight;Node* subR_L = subR->_pLeft;if (pGrandparent == _pHead){pGrandparent->_pLeft = pGrandparent->_pRight = subR;}else{if (subroot == pGrandparent->_pLeft){pGrandparent->_pLeft = subR;}elsepGrandparent->_pRight = subR;}subR->_pParent = pGrandparent;subR->_pLeft = subroot;subroot->_pParent = subR;subroot->_pRight = subR_L;if (subR_L)subR_L->_pParent = subroot;}// 右单旋void RotateR(Node* subroot){Node* pGrandparent = subroot->_pParent;Node* subL = subroot->_pLeft;Node* subL_R = subL->_pRight;if (pGrandparent == _pHead){pGrandparent->_pLeft = pGrandparent->_pRight = subL;}else{if (subroot == pGrandparent->_pLeft){pGrandparent->_pLeft = subL;}elsepGrandparent->_pRight = subL;}subL->_pParent = pGrandparent;subroot->_pLeft = subL_R;if (subL_R)subL_R->_pParent = subroot;subL->_pRight = subroot;subroot->_pParent = subL;}
};

ps.psibling 这个节点是有可能为空结点的，写旋转函数的时候要注意！

3）判断红黑树的合法性

要判断红黑树是否合法就需要比对着红黑树的性质一条一条来确认：

① 红黑树的根节点为 Black ；（⭕需要去判断树的根节点的颜色

② Red 节点不连续，即 Red 节点一定有 Black 的孩子节点；（⭕需要验证

③ 每条路径含有相同数量的 Black 节点；（⭕需要验证

④ 每个节点要么是 Black 的要么是 Red 的；（✅通过enum类型来确保节点黑或红且无其他颜色可能

⑤ nullptr 节点为 Black。（✅这条显然不必验证

思路：选择一条路径并的到这条路径的黑色节点数量，并这条路径的黑色节点数量为标准，判断其他任以路径的黑色节点数量是否与其相等。简单起见，选择最左路径的黑色节点数量为标准数量去比对别的路径的黑色节点数量。

由上，关键问题在于如何计算出所有路径(除选择的标准路径)的外的黑色节点。以下图为例进行分析。

代码示例： 

// 检测红黑树是否为有效的红黑树
bool IsValidRBTRee()
{Node* pCur = _pHead->_pLeft;if (pCur == nullptr)return true;if (pCur->_col == RED)return false;size_t blackNUM = 0;while (pCur){if (pCur->_col == BLACK)++blackNUM;pCur = pCur->_pLeft;}++blackNUM;//算上最后的空节点size_t pathblack = 0;return _IsValidRBTRee(_pHead->_pLeft, blackNUM, pathblack);
}bool _IsValidRBTRee(Node* pRoot, size_t blackCount, size_t pathBlack)
{if (pRoot == nullptr){++pathBlack;//算上最后的空节点if (blackCount == pathBlack)return true;elsereturn false;}if (pRoot->_col == BLACK){++pathBlack;return _IsValidRBTRee(pRoot->_pLeft, blackCount, pathBlack)&& _IsValidRBTRee(pRoot->_pRight, blackCount, pathBlack);}else{if ((pRoot->_pLeft && pRoot->_pLeft->_col == RED)|| (pRoot->_pRight && pRoot->_pRight->_col == RED)){cout << "错误：存在连续的红色节点" << "->" << pRoot->_data << "->该节点附近存在连续红色节点" << endl;return false;}else{return _IsValidRBTRee(pRoot->_pLeft, blackCount, pathBlack)&& _IsValidRBTRee(pRoot->_pRight, blackCount, pathBlack);}}
}

---

END