目录
A. X Axis
B. Matrix Stabilization
C. Update Queries
D. Mathematical Problem
A. X Axis
Problem - A - Codeforces

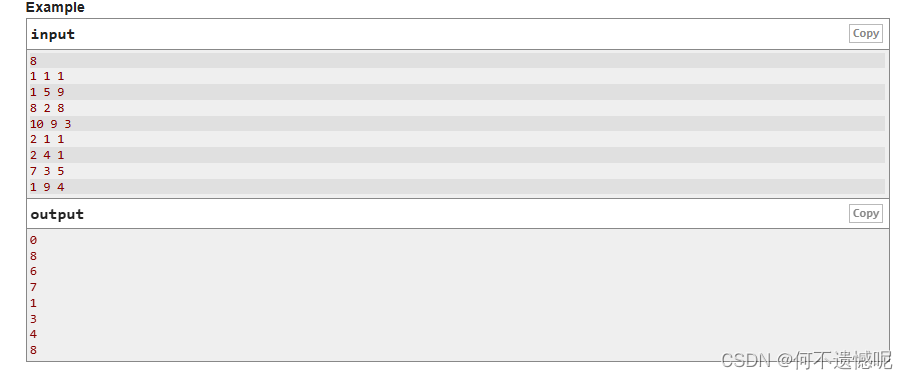
直接找到第二大的数,答案就是这个数与其他两个数的差值的和。
void solve()
{vector<ll>a;for (int i = 1; i <= 3; i++){int x;cin >> x;a.push_back(x);}sort(a.begin(), a.end());cout << a[2]-a[1]+a[1]-a[0] << "\n";}B. Matrix Stabilization
Problem - B - Codeforces

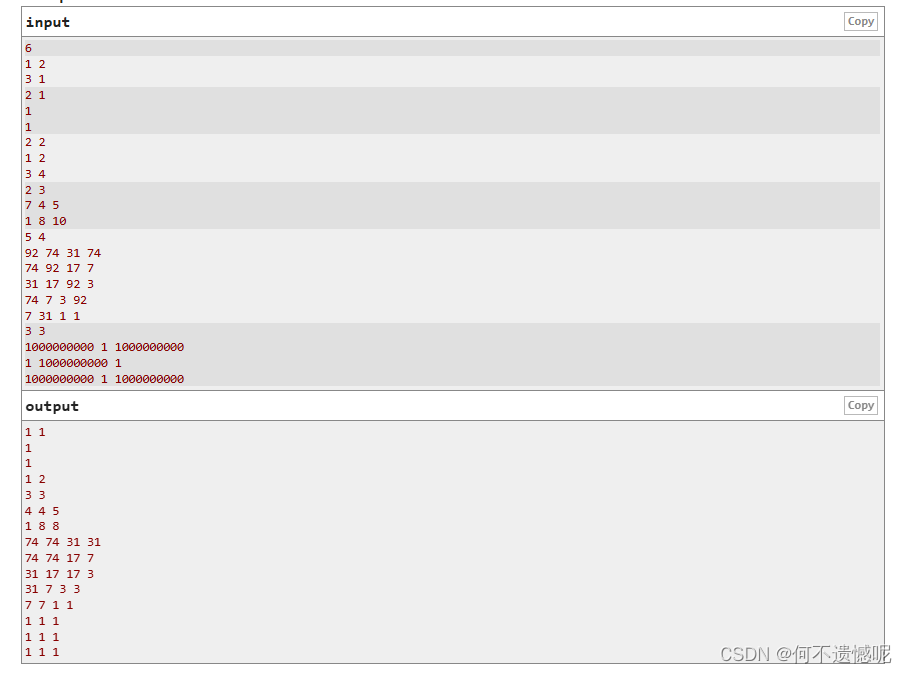
我们发现符合题意的每个数是互不影响的,即改变了其中一个不会影响到另一个,直接找到所以符合题意的数,再将这个数变成周围数的最大值。
int MX(int a, int b, int c, int d)
{vector<int>q;q.push_back(a);q.push_back(b);q.push_back(c);q.push_back(d);sort(q.begin(), q.end());return q[3];
}
void solve()
{memset(f, 0, sizeof(f));int n, m;cin >> n >> m;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){cin >> f[i][j];}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){if (f[i][j] > f[i - 1][j] && f[i][j] > f[i][j - 1] && f[i][j] > f[i + 1][j] && f[i][j] > f[i][j + 1]){f[i][j] = MX(f[i - 1][j], f[i + 1][j], f[i][j - 1], f[i][j + 1]);}}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){cout<< f[i][j]<<" ";}cout << "\n";}cout << "\n";
}C. Update Queries
Problem - C - Codeforces


仔细看就会发现这个操作数组顺序其实没多大关系,只要找到需要操作的所以,再一次填入已经排好序的元素即可。
ll d[200010];
void solve()
{memset(d, 0, sizeof(d));ll n, m;cin >> n >> m;string s1, s2;cin >> s1;int x;for (int i = 1; i <= m; i++) cin >> x, d[x]++;cin >> s2;sort(s2.begin(), s2.end());int c = 0;for (int i = 0; i < s1.size(); i++){if (d[i + 1]&&c<s2.size()){s1[i] = s2[c++];}}cout << s1 << "\n";
}D. Mathematical Problem
Problem - D - Codeforces
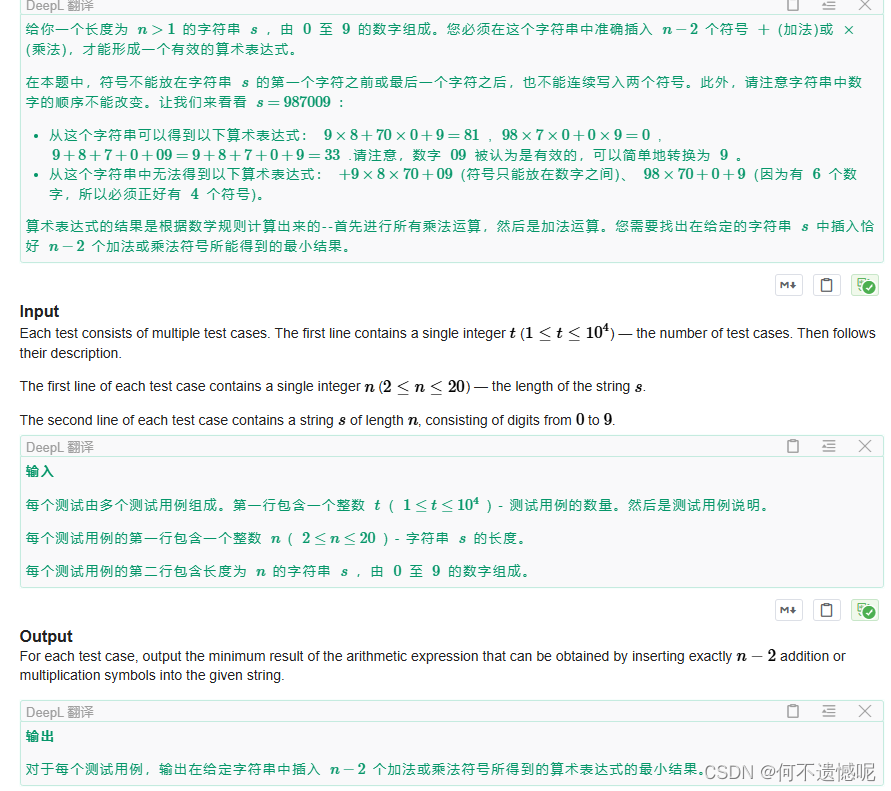
考虑n大于2的情况
当含有元素0时,那么答案就是0,因为可以将他们全部相乘。
当所以元素都为1时,答案就是1,可以全部相乘。
其他情况,答案就是不为1的所有元素的和。
void solve()
{int n;cin >> n;string s;cin >> s;vector<int> cnt(10);int sum = 0;for (int i = 1; i < n; i++) {if (s[i] <= '1') {cnt[s[i] - '0']++;}sum += s[i] - '0';}constexpr int inf = 1e9;int ans = inf;for (int i = 0; i + 2 <= n; i++) {cnt[s[i + 1] - '0']--;sum -= s[i + 1] - '0';int x = stoi(s.substr(i, 2));cout << x << ' ' << sum << ' ' << cnt[0] << ' ' << cnt[1] << '\n';int res;if (cnt[0] + (x == 0) > 0) {res = 0;}else if (cnt[1] + (x == 1) == n - 1) {res = 1;}else {res = (x != 1 ? x : 0) + sum - cnt[1];}ans = min(ans, res);cnt[s[i] - '0']++;sum += s[i] - '0';}cout << ans << '\n';
}