概述
魔兽世界、仙剑奇侠传这类 MMRPG 游戏,不知道你玩过没有?在这些游戏中,有一个非常重要的功能,那就是任务角色自动寻路。当任务处于游戏地图中的某个位置时,我们用鼠标点击另外一个相对较远的位置,任务就会自动绕过障碍物走过去。玩过这么多游戏,不知道你是否思考过,这个功能是怎么实现的呢?
算法解析
实际上,这是一个非常典型的搜索问题。人物的起点就是他当下所在的位置,重点就是鼠标点击的位置。我们需要在地图中,找一条从起点到终点的路径。这条路径要绕过地图中所有障碍物,并且看起来要是一种非常聪明的走法。所谓 “聪明”,笼统地解释就是,走的路不能太绕。理论上讲,最短路径显然是最聪明的做法,是这个问题的最优解。
不过,在最优出行路线规划章节中,我们也讲过,如果图非常大,那 Dijkstra 最短路径算法的执行耗时会很多。在真是的软件开发中,我们面对的是超级大的地图和海量的寻路请求,算法的执行效率太低,这显然是无法接受的。
实际上,像出行路线规划、游戏寻路,这些真是软件开发中的问题,一般情况下,我们都不需要非得求最优解(也就是最短路径)。在权衡线路规划质量和执行效率的情况下,我们只需寻求一个次优解就足够了。那如何快速找出一条接近于最短路线的次优路线呢?
这个快速的路径规划算法,就是本章要学习的 A 算法*。实际上,A* 算法是对 Dijkstra 算法的优化和改造。如何将 Dijkstra 算法改造成 A* 算法 呢?为了更好地理解接下来要将的内容,建议你先温习一下前面章节的 Dijkstra 算法的实现原理。
Dijkstra 算法有点类似 BFS 算法,它每次找到跟起点最近的顶点,往外扩展。这种往外扩展的思路,其实有些盲目。为什么这么说呢?我举个例子来给你解释下。下面这个图对应一个真实的地图,每个顶点在地图中的位置,我们用一个二维坐标 (x,y) 来表示,其中,x 表示横坐标,y 表示纵坐标。
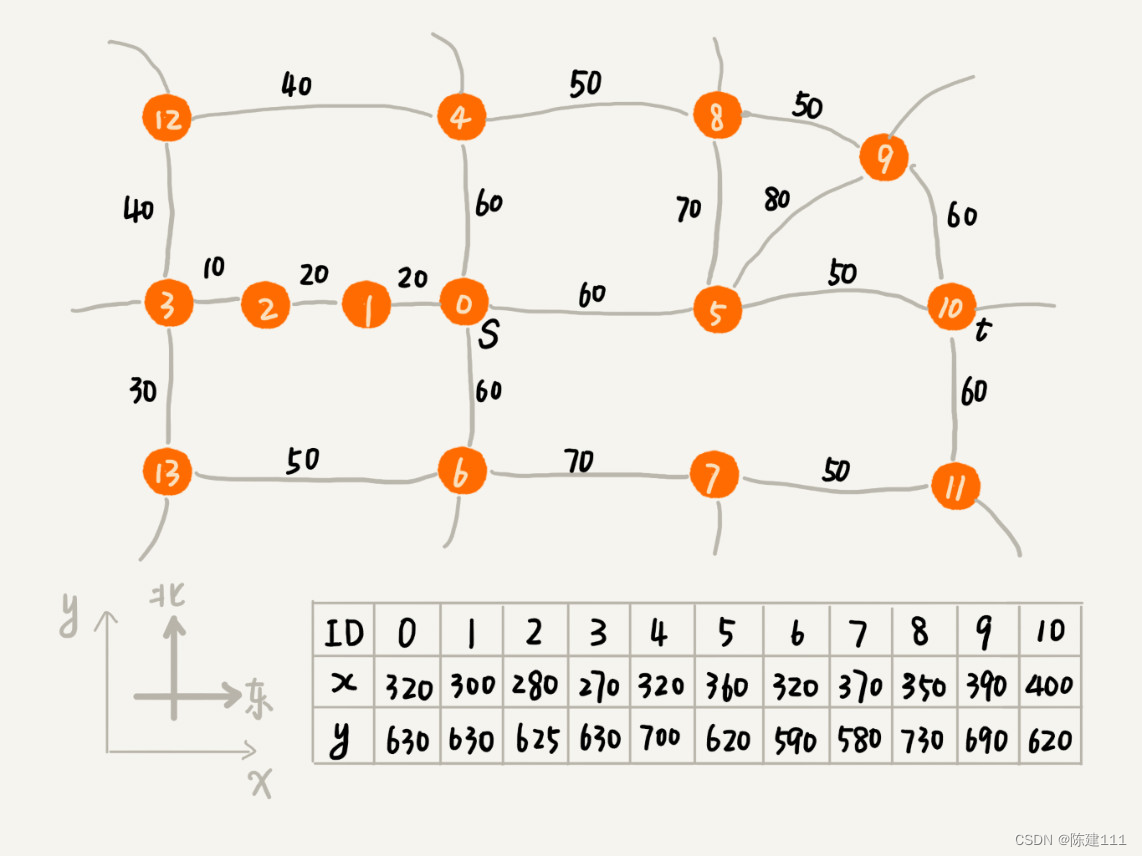
在 Dijkstra 算法的实现思路中,我们用一个优先级队列,来记录已经遍历到的顶点已经这个顶点与起始顶点的路径长度。顶点与起始顶点路径长度越小,就越先被从优先级队列中取出来扩展,从图中举的例子可以看出来,尽管我们找的是 s 到 t 的线路,但是最先被搜搜到的顶点依次是 1,2,3。通过肉眼来观察,这个搜索方向跟我们期望的路线方向(s 到 t 是从西向东)是反着的,路线搜索的方向明显 “跑偏了”。
之所以会跑偏,那是因为我们那是按照顶点与起点的路径长度的大小,来安排出兑顺序的。与顶点越近的顶点,就会越早出队列。我们并没有考虑到这个顶点到终点的距离,所以,在地图中,尽管 1,2,3 三个顶点离起始顶点最近,但是离终点却越来越远。
如果我们综合更多的因素,把这个顶点到终点可能还要走多远,也考虑进去,综合来判断哪个顶点该该先出对,那是不是就可以避免 “跑偏” 呢?
当我们遍历到某个顶点的时候,从起点到这个顶点的路径长度是确定的,我们记作 g(i) (i 表示顶点的编号)。但是从这个顶点到终点的路径长度,我们是未知的,虽然确切的值无法提前知道,但是我们可以用其他估计值来代替。
这里我们可以通过这个顶点跟终点之间的直线距离,也就是欧几里得距离,来近似地估计这个顶点跟终点的路径长度(注意:路径长度和直线距离是两个概念)。我们把这个距离记作 h(i) (i 表示顶点的编号),专业的叫法是启发函数 (heuristic function)。
因为欧几里得距离的计算公式,会涉及比较好使的开根号计算,所以,我们一般通过另外一个更加简单的距离计算公式,那就是曼哈顿距离(Manhattan distance)。曼哈顿距离是两点之间横纵坐标的距离之和。计算的过程只涉及加减法、符号位反转,所以比欧几里得距离更加高效。
int hManhattan(Vertex v1, Vertex v2) {return Math.abs(v1.x - v2.x) + Math.abs(v1.y - v2.y);}
原来只是单纯地通过顶点与起点之间的路径长度 g(i),来判断谁先出队列,现在有了顶点到终点的路径长度估计值,我们通过两者之和 f(i)=g(i)+h(i),来判断哪个顶点先出队列。综合两部分,我们就能有效避免刚刚讲的 “跑偏”。这里 f(i) 的专业叫法是估价函数(evaluation function)。
从刚刚的描述,可以发现,A* 算法就是对 Dijkstra 算法的简单改造。实际上,代码实现方面,我们也只需要稍微改动几行代码,就能把 Dijkstra 算法的代码实现,改成 A* 算法的代码实现。
在 A* 算法的代码实现中,顶点 Vertex 的定义,跟 Dijkstra 算法中的定义,稍微有点儿区别,多了 x、y 坐标,以及刚刚提到的 f(i) 值。图 Grah 类的定义跟 Dijkstra 算法中的定义一样。
private class Vertex {public int id; // 顶点编号public int dist; // 从起始顶点,到这个顶点的距离public int f; // 新增:f(i)=g(i)+h(i)public int x; // 新增:顶点在地图中的横坐标public int y; // 新增:顶点在地图中的纵坐标public Vertex(int id, int x, int y) {this.id = id;this.x = x;this.y = y;this.f = Integer.MAX_VALUE;this.dist = Integer.MAX_VALUE;}}// 新增一个成员变量,在构造函数中初始化private Vertex[] vertexs = new Vertex[this.v];// 新增一个方法,添加顶点的坐标public void addVertex(int id, int x, int y) {vertexs[id] = new Vertex(id, x, y);}
A* 算法的代码实现的主要逻辑是下面这段代码。它跟 Dijkstra 算法的代码实现,主要有 3 点区别:
- 优先级队列构建的方式不同。
A* 算法是根据 f 值(也就是刚刚讲到的f(i)=g(i)+h(i)),来构建优先队列,而 Dijkstra 算法是根据 dist 值(也就是刚讲到的g(i))来构建优先级队列。 A* 算法在更新顶点 dist 值的时候,会同步更新 f 值。- 循环结束的条件也不一样。Dijkstra 算法是在终点出队的时候才结束,
A* 算法是一旦遍历到终点就结束。
public void astra(int s, int t) { // 从顶点s到顶点t的路径int[] predecessor = new int[this.v]; // 用来还原最短路径// 根据vertex的f值构建小顶堆,而不是按照distPriorityQueue queue = new PriorityQueue(this.v);boolean[] inQueue = new boolean[this.v]; // 标记是否进入过队列vertexs[s].dist = 0;vertexs[s].f = 0;queue.add(vertexs[s]);inQueue[s] = true;while (!queue.isEmpty()) {Vertex minVertex = queue.poll(); // 获取对顶元素并删除for (int i = 0; i < adj[minVertex.id].size(); i++) {Edge e = adj[minVertex.id].get(i); // 取出一条minVertex相连的边Vertex nextVertex = vertexs[e.tid]; // minVertex->nextVertexif (minVertex.dist + e.w < nextVertex.dist) { // 更新next的dist,fnextVertex.dist = minVertex.dist + e.w;nextVertex.f = nextVertex.dist + hManhattan(minVertex, vertexs[t]);predecessor[nextVertex.id] = minVertex.id;if (inQueue[nextVertex.id] == true) {queue.update(nextVertex); // 更新队列中的dist} else {queue.add(nextVertex);inQueue[nextVertex.id] = true;}}if (nextVertex.id == t) {queue.clear();break;}}}// 输出最短路径System.out.print(s);print(s, t, predecessor);}
完整的 Graph 代码实现如下所示:
public class Graph {private int v; // 顶点个数private LinkedList<Edge> adj[]; // 邻接表private Vertex[] vertexs; // 新增一个成员变量,在构造函数中初始化public Graph(int v) {this.v = v;this.vertexs = new Vertex[this.v];adj = new LinkedList[v];for (int i = 0; i < adj.length; i++) {adj[i] = new LinkedList<>();}}public void addEdge(int s, int t, int w) { // 添加一条边adj[s].add(new Edge(s, t, w));}// 新增一个方法,添加顶点的坐标public void addVertex(int id, int x, int y) {vertexs[id] = new Vertex(id, x, y);}int hManhattan(Vertex v1, Vertex v2) {return Math.abs(v1.x - v2.x) + Math.abs(v1.y - v2.y);}public void astra(int s, int t) { // 从顶点s到顶点t的路径int[] predecessor = new int[this.v]; // 用来还原最短路径// 根据vertex的f值构建小顶堆,而不是按照distPriorityQueue queue = new PriorityQueue(this.v);boolean[] inQueue = new boolean[this.v]; // 标记是否进入过队列vertexs[s].dist = 0;vertexs[s].f = 0;queue.add(vertexs[s]);inQueue[s] = true;while (!queue.isEmpty()) {Vertex minVertex = queue.poll(); // 获取对顶元素并删除for (int i = 0; i < adj[minVertex.id].size(); i++) {Edge e = adj[minVertex.id].get(i); // 取出一条minVertex相连的边Vertex nextVertex = vertexs[e.tid]; // minVertex->nextVertexif (minVertex.dist + e.w < nextVertex.dist) { // 更新next的dist,fnextVertex.dist = minVertex.dist + e.w;nextVertex.f = nextVertex.dist + hManhattan(minVertex, vertexs[t]);predecessor[nextVertex.id] = minVertex.id;if (inQueue[nextVertex.id] == true) {queue.update(nextVertex); // 更新队列中的dist} else {queue.add(nextVertex);inQueue[nextVertex.id] = true;}}if (nextVertex.id == t) {queue.clear();break;}}}// 输出最短路径System.out.print(s);print(s, t, predecessor);}private void print(int s, int t, int[] predecessor) {if (s == t) return;print(s, predecessor[s], predecessor);System.out.print("->" + t);}// 因为Java提供的优先级队列,没有暴露更新数据的接口,所以,需要重新实现一个private class PriorityQueue { //根据Vertex.f构建小顶堆private Vertex[] nodes;private int count;public PriorityQueue(int v) {this.nodes = new Vertex[v];this.count = v;}public Vertex poll() { /**留给你去实现*/ }public void add(Vertex vertex) { /**留给你去实现*/ }// 更新节点的值,并且从下往上堆化,更新符合堆顶定义。时间复杂度O(logn)public void update(Vertex vertex) { /**留给你去实现*/ }public boolean isEmpty() { /**留给你去实现*/ }public void clear() {for (int i = 0; i < count; i++) {nodes[i] = null;}count = 0;}}private class Vertex {public int id; // 顶点编号public int dist; // 从起始顶点,到这个顶点的距离public int f; // 新增:f(i)=g(i)+h(i)public int x; // 新增:顶点在地图中的横坐标public int y; // 新增:顶点在地图中的纵坐标public Vertex(int id, int x, int y) {this.id = id;this.x = x;this.y = y;this.f = Integer.MAX_VALUE;this.dist = Integer.MAX_VALUE;}}private class Edge {public int sid; // 边的起始顶点编号public int tid; // 边的终止顶点编号public int w; // 权重public Edge(int sid, int tid, int w) {this.sid = sid;this.tid = tid;this.w= w;}}
}
尽管 A* 算法可以更加快速地找到从起点到终点的路线,但是它并不能像 Dijkstra 算法那样,找到最短路径。这是为什么呢?
要找出起点到终点的最短路径,最简单的方法是,通过回溯穷举所有从 s 到达 t 的不同路径,然后对比找出最短的那个。不过很显然,回溯算法的执行效率非常低,是指数级的。

Dijkstra 算法在此基础上,利用动态规划的思想,对回溯搜索进行了剪枝,只保留起点到某个顶点的最短距离,继续往外扩展搜搜。动态规划相较于回溯搜索,只是换了一个实现思路,但它实际上也考察了所有从起点到终点的路线,所以才能得到最优解。

A* 算法之所以不能像 Dijkstra 算法那样,找到最短路径,只要原因是两者的 while 循环结束条件不一样。刚刚讲过,Dijkstra 算法是在终点出队的时候才结束,A* 算法是一旦遍历到终点就结束。对于 Dijkstra 算法来说,当终点出队列的时候,终点的 dist 值是优先级队列中所有顶点的最小值,即便再运行下去,终点的 dist 值也不会再被更新了。对于 A* 算法来说,一旦遍历到终点,我们就结束 while 循环,这个时候,终点的 dist 值未必是最小值。
A* 算法利用贪心算法的思路,每次都找 f 值最小的顶点出队,一旦搜索到终点就不在继续考察其他顶点和路线了。所以,它并没有考察所有的路线,也就不可能找出最短路径了。
搞懂了 A* 算法,我们再来看下,如何借助A* 算法解决今天的游戏寻路问题?
要利用 A* 算法解决这个问题,我们只需把地图,抽象成图就可以了。不过,游戏中的地图跟我们平常将的地图是不一样的。因为游戏中的地图并不像我们现实生活中那样,存在规划非常清晰的道路,更多的是宽阔的视野、草坪等。所以,我们没法把岔路口抽象成定点,把道路抽象成边。
实际上,我们可以换一种抽象思路,把整个地图分割成一个一个的小方块。在某一个方块上的任务,只能往上下左右四个方向的方块上移动。我们可以把每个方块看做一个顶点。两个方块相邻,我们就在它们之间,连两条有向边,并且边的权值都是 1。所以,这个问题就转化成了,在一个有向有全图中,找到某个顶点到另一个顶点的路径问题。将地图抽象成边权值为 1 的有向图之后,我们就可以套用 A* 算法,来实现游戏中任务的自动寻路功能了。
总结
本章讲的 A* 算法属于一种启发式搜索算法(Heuristically Search Algorithm)。实际上,启发式搜索算法并不仅仅只有 A* 算法,还有很多其他算法,比如 IDA* 算法、蚁群算法、遗传算法、模拟退火算法等。如果感兴趣,可以自行研究下。
启发式搜索算法利用估价函数,避免 “跑偏”,贪心地朝着最有可能到达终点的方向前进。这种算法炸出的路线,并不是最短路线。但是,实际的软件开发中的路线规划问题,我们往往并不需要非得找最短距离。所以,鉴于启发式搜索算法能很好地平衡路线质量和执行效率,它在实际的软件开发中的应用更加广泛。实际上,最短路径章节 中讲到的地图 APP 中的出行路线规划问题,也可以利用启发式搜索算法来实现。