一、概率基本知识
1.3 常见概型
1.3.1 古典概型
定义1 古典概型
若随机事件E满足如下两个条件:
(1)样本空间S中只有有限个样本点。
(2)样本空间S中每个样本点发生都是等可能的。
这样的随机试验称为古典概型。
P(A)=A中样本点数/S中样本点数
1.3.2 几何概型
定义2 几何概型
设随机试验E所对应的样本空间S为可度量的有界区域,若所有样本点等可能出现(或样本点出现在S的可度量的子区域上的概率与该区域的几何度量成正比),则称随机试验E所对应的概率类型为几何概型。
P(A)=A的几何度量/S的几何度量
1.3.3 伯努利概型
定义3 伯努利概型
设E为随机试验,若随机试验E,满足:
(1)相同条件下试验可重复进行。
(2)每次试验只有两种可能的结果A与A̅
(3)每次试验A月A̅发生的概率不变。
这样的试验重复进行n次,称其为n重伯努利试验。
1.4 三大概率公式
(一)条件概率
定义1 条件概率
条件概率是一种带有附加条件的概率,例如,如果事件A与事件B是相依事件,即事件A的概率随事件B是否发生而变化,记为P(A|B),表示在事件B发生的条件下,事件A发生的概率,相当于A在B中所占的比例。
计算公式为:
P(A|B)=P(AB)/P(B)
(二)全概率公式
定义2 完备事件组
设随机试验E的样本空间为S,A1,A2…An为一组随机事件,若满足:
(1)事件组A1,A2…An两两互斥。
(2)Un i=1 Ai=S
则称事件组A1,A2…An为一个完备事件组,并有全概率公式:
P(B)=nΣi=1 P(Ai)P(B|Ai)
其中,B为任意事件。
(三)贝叶斯公式
其中P(A|B)是在B发生的情况下A发生的可能性。A1,A2…An为完备事件组,B为任意随机事件,P(B)>0。
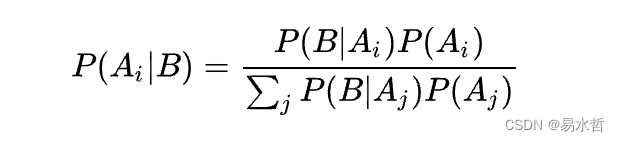
1.5 独立性
定义1 独立性
若随机事件A,B满足P(AB)=P(A)P(B),则称A,B相互独立。
(一)重要结论
事件A与B相互独立
(1)A与B̅ 或A̅与B或A̅与B̅ 相互独立
(2)P(A|B)=P(A)↔P(A|B̅)=P(A)↔P(A|B)=P(A|B̅)(0<P(B)<1)
(3)P(A|B)+P(A̅|B̅)=1(0<P(B)<1)
(4)0概率事件或1概率事件与任意事件均相互独立,从而不可能事件或必然事件与任意事件相互独立。
(5)若事件A与B既相互独立又互不相容,则A与B至少有一个为零概率事件。
(二)独立与互斥的关系
事件A与B独立 P(AB)=P(A)P(B)
A,B互斥↔AB=φ→P(AB)=0
ABC两两独立:
P(AB)=P(A)P(B)
P(AC)=P(A)P©
P(BC)=P(B)P©
ABC相互独立:
P(AB)=P(A)P(B)
P(AC)=P(A)P©
P(BC)=P(B)P©
P(ABC)=P(A)P(B)P©
事件相互独立一定两两独立,反之不成立。