977.有序数组平方
题目链接: 977. 有序数组的平方 - 力扣(LeetCode)文章讲解:代码随想录
视频讲解: 双指针法经典题目 | LeetCode:977.有序数组的平方_哔哩哔哩_bilibili
第一想法
暴力算法肯定是先将元素平方,然后Arrays.sort(),时间复杂度取决于快排O(n logn)
代码随想录
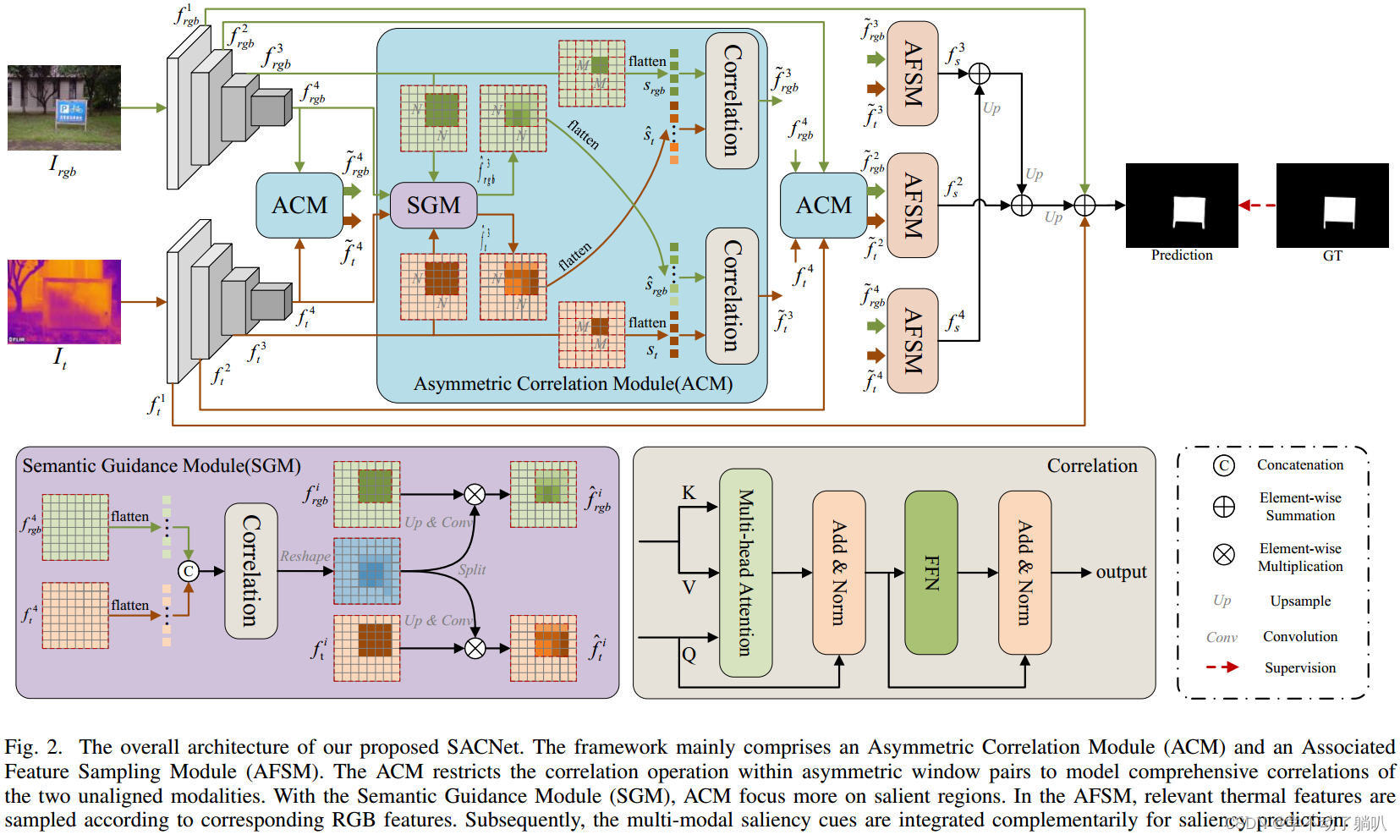
有序数组 [ -5 -3 1 3 5] 按从小到大排列,其平方之后两边一定是最大的,中间一定是最小的,所以定义双头指针,每次筛选出最大值,从新数组result的最大索引处填入。这样更新一轮下来,新数组就会从大到小填好。
定义双头指针比较出最大的元素有些像快速排序算法。
遇到问题
若先将元素更新为平方,然后再用于比较,那么这个元素如果这次尚未选中,下轮就会继续平方。所以这个判断逻辑应放到比较条件里。
代码
class Solution1 {public int[] sortedSquares(int[] nums) {int[] result = new int[nums.length];//定义新数组,大小应与原数组相同int left = 0;int right = nums.length - 1;//定义原数组双头指针int index = nums.length - 1;//定义填充新数组的索引指针for(;left<=right;){//left==right有意义应当进入循环if(nums[left]*nums[left]>nums[right]*nums[right]){result[index--] = nums[left]*nums[left];//若左边元素大,则复制给新数组,左边索引+1left++;}else{result[index--] = nums[right] * nums[right];//若右边元素大,则复制给新数组,右边索引-1;或者两边相同,则选谁填充都无所谓right--;}}return result;}
}209.长度最小的子数组
题目链接: 209. 长度最小的子数组 - 力扣(LeetCode)文章讲解:代码随想录
视频讲解:拿下滑动窗口! | LeetCode 209 长度最小的子数组_哔哩哔哩_bilibili
第一想法
首先一定是暴力想法,逐个数组遍历,若总和满足>=target,则记录数组长度,与上次符合要求的子数组结果作比较,若长度更小,则更新子数组。
代码随想录想法
用一个循环解决问题,那么j指的是子数组的终止位置,其起始位置的确定就在于滑动窗口的策略实现。如果指的是起始位置,那么只有一个一个向后遍历才能返回子数组,思路和暴力解法一致。
移动起始位置的条件是一旦当数组子数组之和>=target之后,起始指针就向后持续移动缩小数组。所以关键在于while循环而非if的单次判断。
一些录友会疑惑为什么时间复杂度是O(n)。
不要以为for里放一个while就以为是O(n^2)啊, 主要是看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)
代码
class Solution1 {public int minSubArrayLen(int target, int[] nums) {int subLength = Integer.MAX_VALUE;int sum = 0;int beginIndex = 0;int endIndex = 0;for(;endIndex<nums.length;endIndex++){sum+=nums[endIndex];//终点指针持续向后移动while (sum>=target){subLength = Math.min(subLength, endIndex - beginIndex + 1);//更新最小长度sum -= nums[beginIndex++];//起始指针后移;}}return subLength == Integer.MAX_VALUE ? 0 : subLength;//若未赋值则返回0}
}59.螺旋矩阵
题目链接: 59. 螺旋矩阵 II - 力扣(LeetCode)文章讲解:代码随想录
视频讲解:一入循环深似海 | LeetCode:59.螺旋矩阵II_哔哩哔哩_bilibili
第一想法
没思路,一碰到循环和二维数组就寄
代码随想录思路
确定圈数:n/2,因为每转一圈,边长-2
n%2==1,有余数的话,最后一圈只要一个元素
每条边的处理都遵循左闭右开的原则,第一个节点留给此边处理,最后一个结点留给下一条边处理。
别人优化思路
1.关于中心元素处理:其实可以在初始化res矩阵的时候就直接把全部元素初始化为n*n,这样即使n是奇数,也无需处理中间的元素
2.startx,starty,offset可以优化成一个变量处理。
代码
画了一下四个边角的坐标,数组的边界处理,这个offset变量还是很难把握
class Solution {public int[][] generateMatrix(int n) {int[][] result = new int[n][n];//新建二维数组int loop = 0;int startX = 0, startY = 0, offset = 1;//起始X坐标,起始Y坐标,偏移量int count = 1;while (loop<n/2){int i = startX, j = startY;//先处理上边界for (j = startY; j < n - offset; j++) {//j的最大值应该是倒数第二个元素j<=n-1-offset,即j<n-offsetresult[startX][j] = count++;}//处理右边界for (i = startX; i < n - offset; i++) {//此时j等于n-offsetresult[i][j]=count++;}//处理下边界for(;j>startY;j--){result[i][j]=count++;}//处理左边界for(;i>startX;i--){result[i][j]=count++;}startX++;startY++;offset++;loop++;}if(n%2==1){result[startX][startY]=count;}return result;}
}