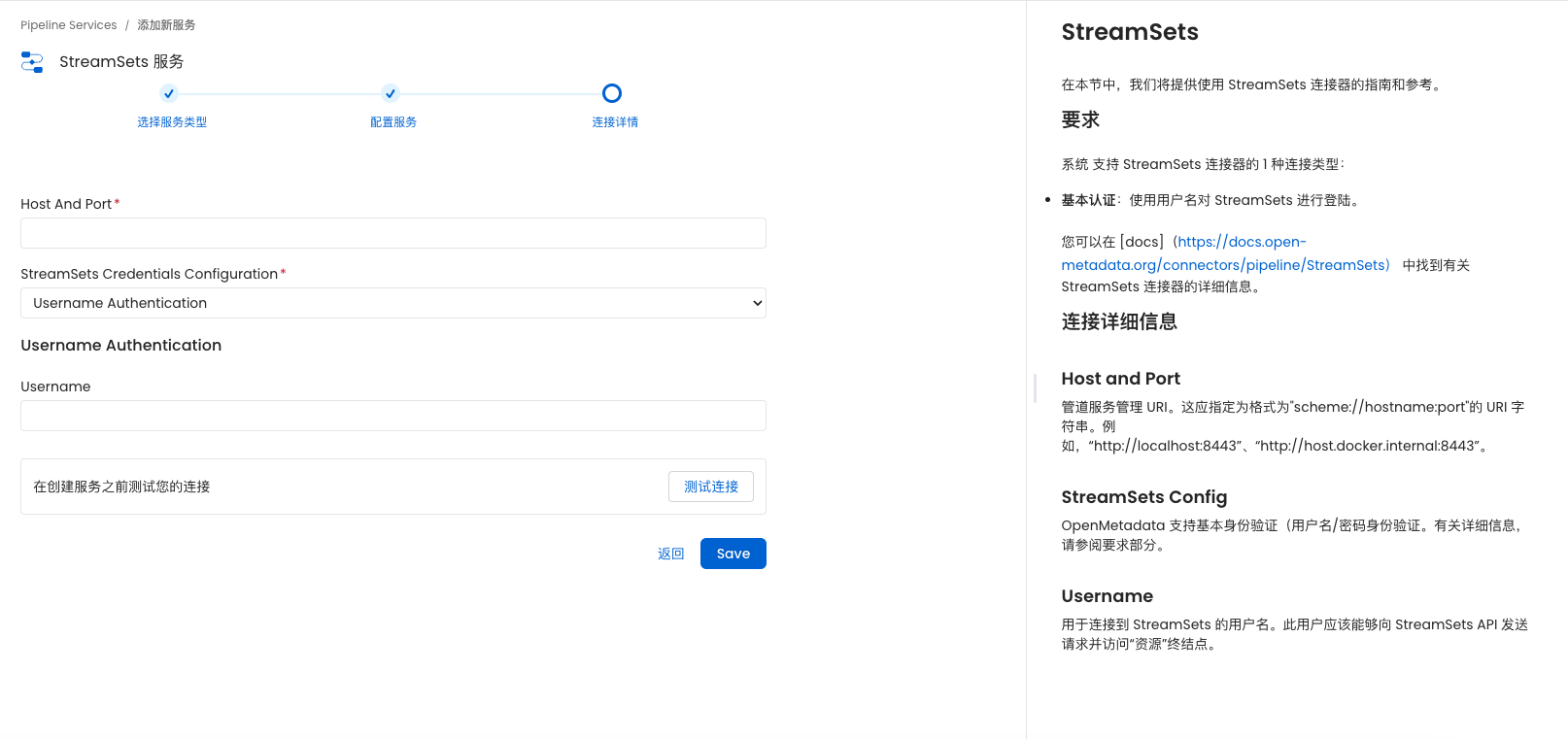
差分约束
(1) 求不等式组的可行解
- 源点:从源点出发,一定可以走到所有的边
- 求可行解步骤:
- 先将每个不等式 x i ≤ x j + c x_i \le x_j + c xi≤xj+c,转化成一条从 s j s_j sj走到 s i s_i si,长度为 c k c_k ck 的一条边
- 找一个超级源点,使得该源点一定可以遍历到所有边
- 从源点求一遍单源最短路
- 结果一:如果存在负环,则原不等式组一定无解
- 结果二:如果没有负环,则 d i s t [ i ] dist[i] dist[i]就是原不等式组的一个可行解
(2) 如何求最大值或最小值
- 结论: 如果求的是最小值,则应该求最长路;如果求的是最大值,则应该求最短路;
- 问题1:如何转化 x i ≤ c x_i \le c xi≤c,其中c是一个常数
- 方法:建立一个超级源点,0,然后建立0->i,长度是c的边即可。
- 以求 x i x_i xi的最大值为例:求所有从 x i x_i xi出发,构成的不等式链 x i ≤ x j + c j ≤ x k + c 2 + c 1 ≤ . . . ≤ c 1 + c 2 + . . . x_i \le x_j+c_j \le x_k + c_2 + c_1 \le ...\le c_1+c_2+... xi≤xj+cj≤xk+c2+c1≤...≤c1+c2+...所计算出的上界(而这个上界要让所有关系都成立,那么就必须以最小的上界为上界,因此需要用最短路算法求到i这个点的最短距离)
(3) 关系:
每一个差分约束的问题都可以转换成最短路的问题
理论理解
题单
1. 糖果
第一眼:
- 感觉和floyd的排序那一道题有点相似之处,两个点之间都有关系(ps:关系闭包)
- 和排序不一样的地方在于,这道题确定小朋友各种胡搅蛮缠的糖多糖少要求后,老师需要准备的糖个数的最小值
思考:
- 怎么去结合这两种题目要求呢,一开始能想到的处理就是先处理关系闭包问题,同时用一个ans去记录老师需要准备的糖的数量从最少的1个开始,关系环到一个一个往后的大于关系也只是加1(这个时候又想到记录方案数那题),如果是相等的关系,当前节点的方案数是前一点的一倍,如果大于关系,当前节点的方案数等于前个节点加一,最后老师需要准备糖果的个数就是总的方案数,该觉还是可以spfa走一波,开一个cnt数组那样子
- 这样要怎么考虑所有关系呢
听y说:
- 二刷视频
- 我悟了。就是这题它并没有直接给出我需要给某个小朋友多少糖,只给出了每个小朋友糖的相对数量关系,而我们需要一个超级源点,去遍历到所有的边。
- 关于求最小值用最长路建边并做spfa求最长路,
#include<bits/stdc++.h>using namespace std;
#define int long long
int n,k;
const int N=1e5+10,M=3*N;
int h[N],e[M],ne[M],w[M],idx;
int d[N],q[N],st[N],cnt[N];void add(int a,int b,int c){e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}bool spfa(){memset(d,-0x3f,sizeof d);d[0]=0;int hh=0,tt=1;q[hh]=0;while(hh!=tt){int t=q[--tt];if(tt==N) tt=0;st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(d[j]<d[t]+w[i]){d[j]=d[t]+w[i];cnt[j]=cnt[t]+1;if(cnt[j]>=n+1) return 0;if(!st[j]){st[j]=1;q[tt++]=j;if(tt==N)tt=0;}}}}return 1;
}signed main(){scanf("%lld%lld",&n,&k);memset(h,-1,sizeof h);for(int i=0;i<k;i++){int x,a,b;scanf("%lld%lld%lld",&x,&a,&b);if(x==1) add(b,a,0),add(a,b,0);else if(x==2) add(a,b,1);else if(x==3) add(b,a,0);else if(x==4) add(b,a,1);else if(x==5) add(a,b,0);}for(int i=1;i<=n;i++) add(0,i,1);int res=spfa();if(!res){puts("-1");}else{res=0;for(int i=1;i<=n;i++) res+=d[i];printf("%lld",res);}return 0;
}
用先进先出的栈
2. 区间
第一眼:
- 如果要让Z包含的数尽可能少,那就让一个区间的数集中在和其他区间相交的部分就可以贪心的解决这个问题了吧
听y说:
- 用差分约束的思想做很牛逼,同时利用前缀和的思想,绝绝子
- 两个端点约束关系:
- s [ i ] ≥ s [ i − 1 ] s[i] \ge s[i-1] s[i]≥s[i−1]
- $s[i]-s[i-1] \le 1 $
- [ a , b ] [a,b] [a,b] s [ b ] − s [ a − 1 ] ≥ c s[b]-s[a-1] \ge c s[b]−s[a−1]≥c
- 转换成最短路模型——求最长路
- s [ i ] ≥ s [ i − 1 ] s[i] \ge s[i-1] s[i]≥s[i−1]
- s [ i − 1 ] ≥ s [ i ] − 1 s[i-1] \ge s[i] -1 s[i−1]≥s[i]−1
- s [ b ] ≥ s [ a − 1 ] + c s[b] \ge s[a-1]+c s[b]≥s[a−1]+c
- 接着就是模版框框的打了
#include<bits/stdc++.h>using namespace std;
//关于这里的N和M的取值,因为M代表边数,我们以最大值N建边
//最多会建3*N条边,如果也算上第N个点的位置的话,会数组越界,可以开大一个数量级
//因为并没有特别熟练空间复杂度以及并不料想到后他数据怎么卡,就开大一个数量级过了
const int N=5e4+10,M=4*N+10;
int m;
int h[N],e[M],w[M],ne[M],idx;
int d[N],st[N],cnt[N],q[N];void add(int a,int b,int c){e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}bool spfa(){memset(d,-0x3f,sizeof d);d[0]=0;int hh=0,tt=1;while(hh!=tt){int t=q[hh++];if(hh==N) hh=0;st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(d[j]<d[t]+w[i]){d[j]=d[t]+w[i];if(!st[j]){st[j]=1;q[tt++]=j;if(tt==N) tt=0;}}}}}signed main(){scanf("%d",&m);memset(h,-1,sizeof h);for(int i=1;i<N;i++){add(i-1,i,0);add(i,i-1,-1);}while(m--){int a,b,c;scanf("%d%d%d",&a,&b,&c);a++,b++;add(a-1,b,c);}spfa();printf("%d",d[50001]);return 0;
}
3. 排队布局
第一眼:
- 又是usaco的牛,好多事的牛
- 1和n之间可以任意大,说明1或n都没有能够约束他们的其他牛
- 不存在满足要求,是不是两头牛之间的约束关系会存在矛盾
思考:
学差分约束的时候时把这道题和糖果(第一题)进行着对比来学的
- 糖果——求最小值——求最长路
- 本题——求最大值
索性先自己思考并落实一遍
- 两头牛之间距离差分约束关系
- 原本编号的先后顺序: s [ i ] < = s [ i + 1 ] s[i]<=s[i+1] s[i]<=s[i+1]
- 前 M L M_L ML条边: s [ a ] − s [ b ] ≤ c s[a]-s[b] \le c s[a]−s[b]≤c
- 后 M D M_D MD条边: s [ a ] − s [ b ] ≥ c s[a]-s[b] \ge c s[a]−s[b]≥c
- 最短路;
- s [ i ] < = s [ i + 1 ] s[i]<=s[i+1] s[i]<=s[i+1]
- s [ a ] ≤ s [ b ] + c s[a] \le s[b]+c s[a]≤s[b]+c
- s [ b ] ≤ s [ a ] − c s[b] \le s[a]-c s[b]≤s[a]−c
- Tips:
为什么n一定能到其他所有边?
- 因为第一条约束关系
隐含的前缀和思想
#include<bits/stdc++.h>using namespace std;
//需要思考怎么建边,约束条件如何化成边
const int N=1e3+10,M=2e4+10+2*N,INF=0x3f3f3f3f;
int n,l,d;
int h[N],e[M],w[M],ne[M],idx;
int dist[N],st[N],cnt[N],q[N];void add(int a,int b,int c){e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}int spfa(int s){memset(dist,0x3f,sizeof dist);memset(st,0,sizeof st);memset(cnt,0,sizeof cnt);dist[s]=0;int hh=0,tt=1;q[hh]=s;while(hh!=tt){int t=q[hh++];if(hh==N) hh=0;st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i]; if(dist[j]>dist[t]+w[i]){dist[j]=dist[t]+w[i];cnt[j]=cnt[t]+1;if(cnt[j]>=n+1) return -1;if(!st[j]){st[j]=1;q[tt++]=j;if(tt==N) tt=0;}}}}return 1;
}signed main(){cin>>n>>l>>d;memset(h,-1,sizeof h);for(int i=1;i<n;i++){add(i+1,i,0);add(0,i,0);}add(0,n,0);for(int i=0;i<l;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);if(a>b) swap(a,b);add(a,b,c);}for(int i=0;i<d;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);if(a>b) swap(a,b);add(b,a,-c);}int res=spfa(0);if(res==-1) puts("-1");else{spfa(1);printf("%d",dist[n]==INF?-2:dist[n]);}return 0;
}

4. 雇佣收银员
第一眼:
- 感觉和区间会很像,一个时间段如果需要很多营业员,那么就让每个营业员的工作时间尽可能覆盖到这个区间
- 输入处理比较麻烦(第二眼,实际上还好,就是变量表示需要思考一下
思考:
建边操作:
用区间表示所需,采用前缀和来建立关系:
某一时刻的营收员人数要大于等于这一时刻所需要的营收员人数
上岗人数不能超过申请人数
以时刻作为点
i时刻所需,i时刻申请,像是隐含的关系,就是一个人工作时长导致的区间内申请人数的变化仍然需要满足能够在某时刻大于等于所需的人数
然后是某一时刻的申请人数也可以用前缀和来表示,于是可以x[i]的建边也可以用 s u m [ i ] − s u m [ i − 1 ] sum[i]-sum[i-1] sum[i]−sum[i−1]来表示
s u m [ i ] sum[i] sum[i] x [ i ] x[i] x[i] r [ i ] r[i] r[i] n u m [ i ] num[i] num[i]
上岗人数约束关系如下:
- 某一时刻的上岗人数 : s u m [ i ] − s u m [ i − 1 ] > = 0 sum[i]-sum[i-1]>=0 sum[i]−sum[i−1]>=0
- 某一时刻的上岗和申请人数之间的关系: s u m [ i ] − s u m [ i − 1 ] ≤ n u m [ i ] sum[i]-sum[i-1]\le num[i] sum[i]−sum[i−1]≤num[i]
- 某一时刻的所在的上岗人数,
- [ 1 , 7 ] [1,7] [1,7]: s u m [ i ] + s u m [ 24 ] − s u m [ 24 − ( 7 − i ) ] > = r [ i ] sum[i]+sum[24]-sum[24-(7-i)]>=r[i] sum[i]+sum[24]−sum[24−(7−i)]>=r[i]即 s u m [ i ] + s u m [ 24 ] − s u m [ 16 + i ] > = r [ i ] sum[i]+sum[24]-sum[16+i]>=r[i] sum[i]+sum[24]−sum[16+i]>=r[i]
- [ 8 , 24 ] [8,24] [8,24]: s u m [ i ] − s u m [ i − 8 ] > = r [ i ] sum[i]-sum[i-8]>=r[i] sum[i]−sum[i−8]>=r[i]
转换成最短路模型如下:
- s u m [ i ] > = s [ i − 1 ] sum[i]>=s[i-1] sum[i]>=s[i−1]
- s u m [ i − 1 ] > = s u m [ i ] − n u m [ i ] sum[i-1]>=sum[i]-num[i] sum[i−1]>=sum[i]−num[i]
- s u m [ i ] > = s u m [ 16 + i ] − s u m [ 24 ] + r [ i ] sum[i]>=sum[16+i]-sum[24]+r[i] sum[i]>=sum[16+i]−sum[24]+r[i]
- s u m [ i ] > = r [ i ] + s u m [ i − 8 ] sum[i]>=r[i]+sum[i-8] sum[i]>=r[i]+sum[i−8]
#include<bits/stdc++.h>using namespace std;
const int N=30,M=100;
int n,sum[N],r[N],num[N];
int h[N],e[M],ne[M],w[M],idx;
int cnt[N],st[N],q[M],d[N];void add(int a,int b,int c){e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}void build(int c){memset(h,-1,sizeof h);idx=0;for(int i=1;i<=24;i++){add(i-1,i,0);add(i,i-1,-num[i]);}for(int i=1;i<=7;i++) add(16+i,i,r[i]-c);for(int i=8;i<=24;i++) add(i-8,i,r[i]);add(0,24,c),add(24,0,-c);
}bool spfa(int s24){memset(d,-0x3f,sizeof d);memset(st,0,sizeof st);memset(cnt,0,sizeof cnt);build(s24);int hh=0,tt=1;d[0]=0;q[0]=0;while(hh!=tt){int t=q[hh++];if(hh==N) hh=0;st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(d[j]<d[t]+w[i]){d[j]=d[t]+w[i];cnt[j]=cnt[t]+1;if(cnt[j]>=25) return false;if(!st[j]){st[j]=1;q[tt++]=j;if(tt==N) tt=0;}}}}return true;
}signed main(){int t;cin>>t;while(t--){memset(num,0,sizeof num);for(int i=1;i<=24;i++){scanf("%d",r+i);}cin>>n;while(n--){int x;scanf("%d",&x);num[x+1]++;}int res=0;for(int i=0;i<=1000;i++){//res=spfa(i);if(spfa(i)){res=1;cout<<i<<endl;break;}}if(!res)puts("No Solution");}return 0;
}
2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
4
0
8
16
16