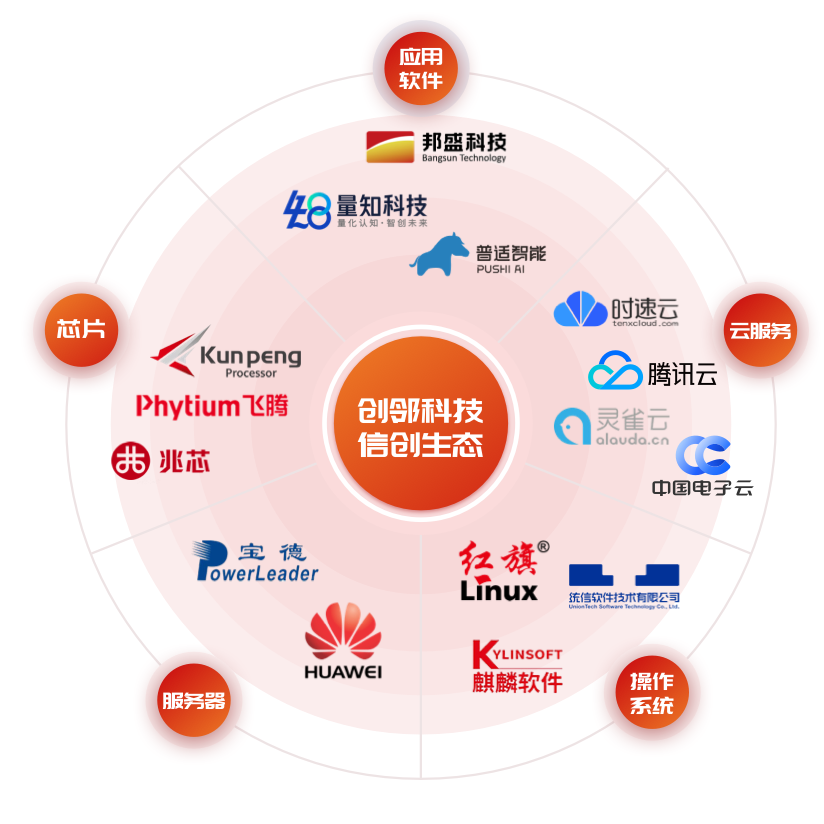
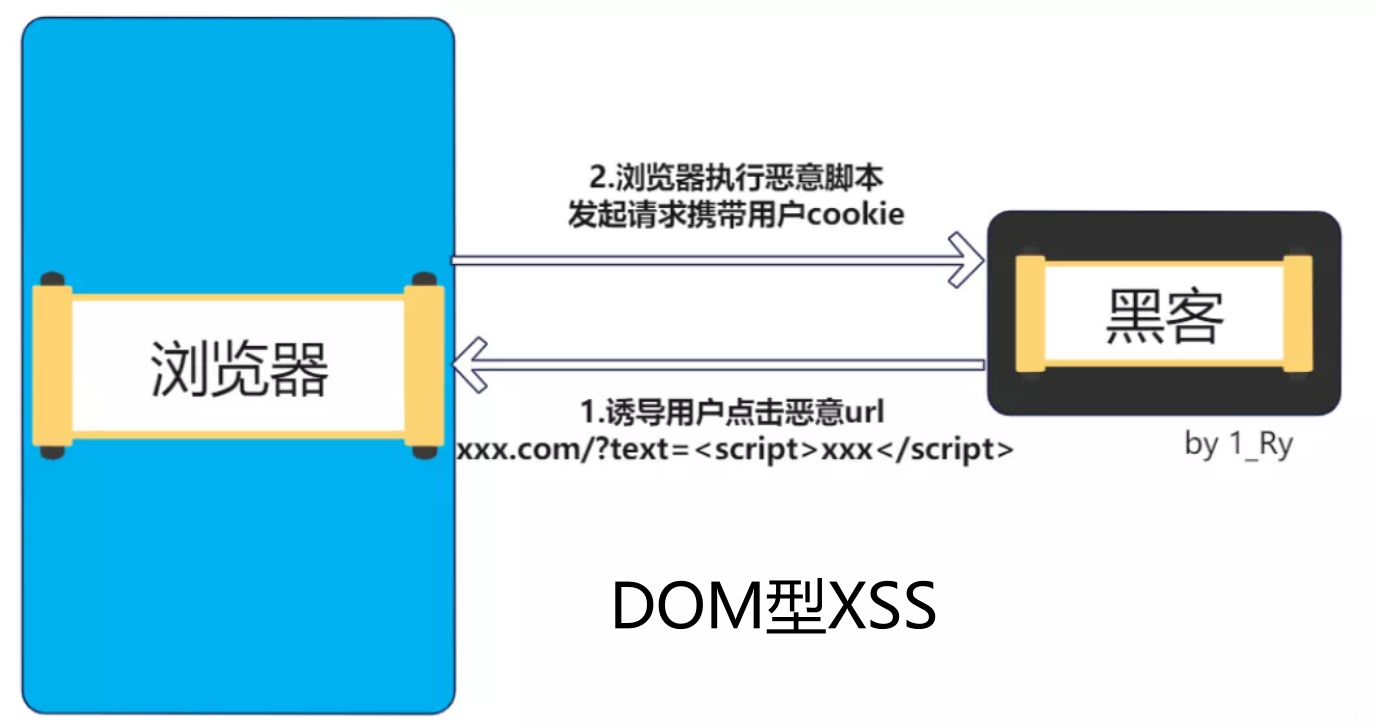
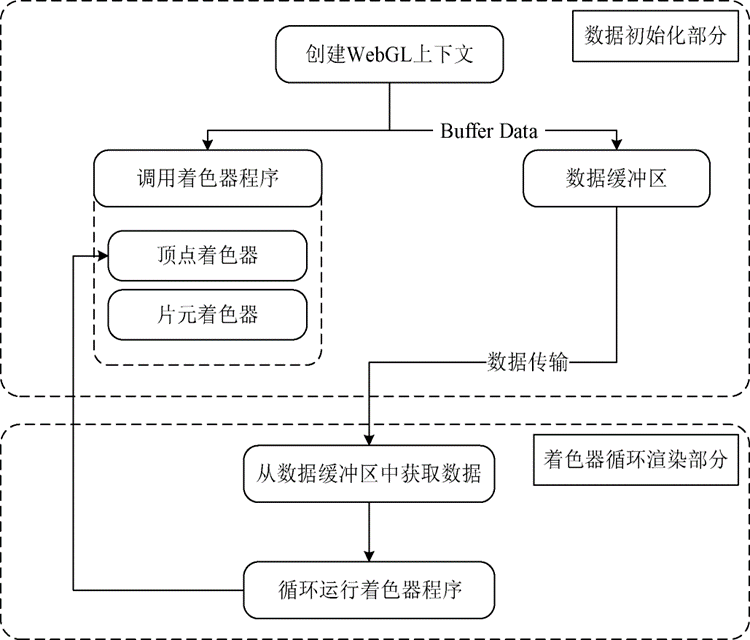
信号实现运算,首先要明确,电路此时为负反馈电路,当处于深度负反馈时,可直接使用虚短虚断。负反馈相关内容可见:放大电路中的反馈_基极反馈-CSDN博客![]() https://blog.csdn.net/qq_63796876/article/details/140438759
https://blog.csdn.net/qq_63796876/article/details/140438759
一、反相比例运算电路
电路:

up 和 un 虚短,都是0V(虚短是因为深度负反馈);up 和 un 又虚断,所以理想状态下 in 和 ip 都为0(这是运放本身的性质)。然后即可得 uo 。
uo = ( -Rf / R1 ) * ui
R2 = R1 // Rf(原因:理想状态下,上图中 ui = 0 时,uo = 0 ,但实际上,此时仍然存在小的静态电流(可以理解为运放输入端的差分电路影响的),会使 un ≠ 0 ,影响到输出 uo 。为了使此情况下 uo 等于 0 ,加入 R2,其值为 R1 和 Rf 并联,就可以在不输入信号时,uo 为0,R2 称为平衡电阻)
可以看出,uo 和 ui 相比多了负号,即 “反相” 。
二、同相比例运算电路
电路:

与反相比例运算电路一样,利用虚短虚断计算 uo 和 ui 的关系。
uo = ( 1+ Rf / R1 )*ui
R2 = R1 // Rf ( R2 为平衡电阻)
uo 和 ui 同相。
三、思考1:同相比例运算电路和反相比例运算电路区别
同相比例运算电路和反相比例运算电路的区别,直观一些的就是输出信号和输入信号相位关系,除此外,可以从输入电阻和共模差模信号看:
上图的反相比例运算电路由于虚短, up = un = 0 ,即 un 虚地,那么不存在共模信号;而输入电阻为 R(可以通过电压/电流得知),与运放的无穷大的输入电阻相比,输入电阻变小,这是不利条件。综上,选择运放时,不需要太注重共模抑制比。而针对输入电阻小的问题,可以看下负反馈文章中提到的输入电阻自举补偿。
而同相比例运算电路,按照上面的分析方法:存在共模信号;但输入电阻很大,很适合采集电压信号;放大倍数一定大于1。选择运放信号的时候,要注重共模抑制比。
除上述,有的电路还需要注重开环增益 A 的大小。
四、电压跟随器
电路:

uo = ui
输入电阻大,输出电阻小,适合采集电压,但存在共模信号。
五、求和运算电路
反相求和运算电路:


由各个信号源看进去的输入电阻不同。
同相求和运算电路:

满足上述图片中所写条件时:

六、加减运算电路
电路:

满足上述图片中所写条件时:

七、差分比例运算电路
当加减运算电路只有两个输入时,则为差分比例运算电路。
电路:

ui2 侧加上 Rf ,Ri2 = R + Rf ,去掉 Rf 后,ui2 的输入电阻就变为了无穷大,即加上 Rf 后,输入电阻变小了。
与之对应的解决方案为,使用两级电路:

八、积分运算电路和微分运算电路
积分运算电路:
反相积分:

同相积分:

积分电路可以实现方波、三角波波形变换,正余弦移项功能。
微分运算电路:

实用微分运算电路:

此电路产生原因:使用基本微分电路,刚上电时(阶跃信号),电容电流近似于无穷大,根据虚短虚断,通过电阻 R 产生的 uo 很大,会使运放内部的放大管进入饱和或者截止状态,即使信号消失,管子也不能回到放大区,出现阻塞现象。同时,由于反馈网络为滞后环节,它与运放内部的滞后环节叠加,易自激振荡,使电路不稳定。
所以解决:使用 R1 限制电容 C 的电流,使用电容值较小的 C1 进行相位补偿(这里说的较小是相比于电容 C ),使用双向稳压管对输出的 uo 进行限制(为什么是双向,因为要根据输入信号 ui 的正负使管子起作用)。
九、PID调节器

十、电路设计思想
说完了上述的几种电路,我们来说两种设计电路的思想:
1、根据各个元件电压与电流的关系设计电路

看着图片,重新看比例电路和微积分电路,相信会有不同的感受。
2、学会将电路进行逆运算

实例:

同时,还有开方运算等。
十一、对数运算电路和指数运算电路
按照上述提到的设计电路的方法1,来看对数运算电路和指数运算电路。
对数运算电路
使用二极管的对数运算电路:

运算精度受到温度影响(体现在 UT 和 Is 上),而且二极管在电流较小时内部载流子的复合运动不可忽略,电流较大时内阻不可忽略,所以在一定电流范围内才满足指数特性,为了扩大输入电压的动态范围,所以用晶体管代替二极管。
使用晶体管的对数运算电路:

同样, 运算精度受到温度影响(体现在 UT 和 Is 上),下面介绍集成电路内部:

指数运算电路

集成电路内部:

十二、乘法运算电路和开方运算电路
乘法运算电路
我们已经学过了加减、微积分、对数指数电路,那么接下来我们要通过学过的这些电路,设计出乘法电路:

电路符号:

uo = k * ux * uy(k可正可负,具体看乘法器型号)
乘法电路已经有了,如果我想算 ui 的10次方呢?大概思路如下:
ui --> ln ui -->乘10--> 10 ln ui --> 指数运算--> 得到 ui 的10次方
开方运算电路
根据乘法器,我们也能算开方:(使用电路设计思想中的2)

假如没有上图中的二极管 D ,且 ui >0 ,k > 0,那么就不会是负反馈,而是正反馈(只有当 ui <0 时,才为负反馈),当处于正反馈时,运放内部的晶体管工作到截至区或者饱和区,出现闭锁现象,为了防止这种现象出现,在输出回路中串联一个二极管。当 ui 为正时,运放输出为负,二极管关断,信号无法向后输送。
十三、仪表放大器
仪表放大器又叫精密放大器,用于弱信号的放大,比如放大传感器的输出电压。
三运放构成的精密放大器:

R2的作用可以通过计算有 R2 和没有 R2 时的共模放大倍数,差模放大倍数比较。
仪表集成放大器:
下面为型号INA102内部电路图:

可以认真与三运放构成的精密放大器比较