原题链接:F. Sonya and Bitwise OR
题目大意:
给出一个长度为 n n n 的数组 a a a,并给出 m m m 次询问以及一个数字 x x x。
每个询问形式如下给出:
- 1 1 1 i i i y y y :将 a i a_{i} ai 位置的值更改为 y y y 。
- 2 2 2 l l l r r r :询问在数组区间 [ l , r ] [l, r] [l,r] 内有多少个子区间 [ L , R ] [L,R] [L,R] 满足 l ≤ L ≤ R ≤ r l \leq L \leq R \leq r l≤L≤R≤r ,且 a L o r a L + 1 o r . . . o r a R − 1 o r a R ≥ x a_{L} or \space a_{L+1} or \space ... \space or \space a_{R-1} or \space a_{R} \geq x aLor aL+1or ... or aR−1or aR≥x(其中 o r or or 表示二进制下的 或 操作)。
解题思路:
乍一看好像没什么很好做的方法,先考虑最暴力的做法是怎么做。
显然,对每个询问,枚举左端点 L L L 暴力向右找右端点 R R R 统计的总复杂度为 O ( m n 2 ) O(mn^{2}) O(mn2) 。
显然,对右端点的查询,我们做一个二分的优化复杂度可以变成 O ( m n log n ) O(mn \log n) O(mnlogn),足够好了,但仍然无法通过。
考虑进一步挖掘一下性质,我们可以发现或操作是单调递增的,即只要某一个位置从 0 0 0 变成 1 1 1 后,则单调保持不变。
进一步思考,因为值域 V ∈ [ 0 , 2 20 ) V \in [0,2^{20}) V∈[0,220),那么我们的前缀或最多会变化 O ( log V ) O(\log V) O(logV) 次,即最多会有 20 20 20 个位置有用(在这次 o r or or 操作时,补上了某个位使 0 0 0 变 1 1 1)。
我们只需要记录这些存在变化的位置,定下 L L L 之后让 R R R 在这些变化后的位置暴力枚举即可,可知我们最多只会枚举 O ( log V ) O(\log V) O(logV) 次。
那问题来了,我们要怎么高效获取某个区间内哪些位置出现变化从而减少复杂度呢?答案很显然,线段树。
线段树内每个节点维护一个 v e c t o r vector vector 保存这个区间内,前/后缀出现变化的位置和其下标。
考虑如何维护区间的 v e c t o r vector vector:
- 假设以及维护好了 [ l , m i d ] , [ m i d + 1 , r ] [l,mid],[mid+1,r] [l,mid],[mid+1,r] 的信息,现在将信息上推至 [ l , r ] [l,r] [l,r] 。
- [ l , r ] [l,r] [l,r] 的前缀或信息即 [ l , m i d ] [l,mid] [l,mid] 的前缀或的信息再继续不断或上 [ m i d + 1 , r ] [mid+1,r] [mid+1,r] 的前缀或信息,假设或的过程中发现某个位置的比特位出现变化,则 p u s h b a c k push_back pushback 其位置的值和下标进 v e c t o r vector vector 内,可知枚举的位置总个数不会超过 O ( l o g V ) O(log V) O(logV) 个。
- [ l , r ] [l,r] [l,r] 的后缀或信息即 [ m i d + 1 , r ] [mid+1,r] [mid+1,r] 的后缀或的信息再继续不断或上 [ l , m i d ] [l,mid] [l,mid] 的后缀或信息,假设或的过程中发现某个位置的比特位出现变化,则 p u s h b a c k push_back pushback 其位置的值和下标进 v e c t o r vector vector 内,可知枚举的位置总个数不会超过 O ( l o g V ) O(log V) O(logV) 个。
考虑答案如何获取,我们采用一个分治的思想:

- 假设我们已经计算完了 [ l , m i d ] , [ m i d + 1 , r ] [l,mid],[mid+1,r] [l,mid],[mid+1,r] 的答案,现在将计算横跨 m i d mid mid 的 [ l , r ] [l,r] [l,r] 的答案。
- 我们已知 [ l , m i d ] [l,mid] [l,mid] 的后缀或数组,以及 [ m i d + 1 , r ] [mid+1,r] [mid+1,r] 的前缀或数组 L L L 。
- 我们考虑设置两个双指针 L , R L,R L,R ,一个放在 [ l , m i d ] [l,mid] [l,mid] 的后缀数组 A A A 内,一个放在 [ m i d + 1 , r ] [mid+1,r] [mid+1,r] 的前缀数组 B B B 内,那么显然我们可以枚举 L L L,然后寻找 R R R。
- 查询 [ L , R ] [L,R] [L,R] 的区间或是否 ≥ x \geq x ≥x,即查询是否存在 A [ L ] o r B [ R ] ≥ x A[L] or B[R] \geq x A[L]orB[R]≥x,满足条件时答案直接加上 r − B [ R ] . s e c o n d + 1 r-B[R].second+1 r−B[R].second+1,同时左指针右移( B [ R ] . s e c o n d B[R].second B[R].second 对应原数组内的即下标)。
- 否则 < x < x <x 时右指针 R R R 向右移动直到满足答案为止。
这样,我们信息上推的复杂度就是 O ( log n log V ) O(\log n \log V) O(lognlogV) 的,单次查询也是 O ( log n log V ) O(\log n \log V) O(lognlogV) 的,修改直接照常修改即可,复杂度同时也是 O ( log n log V ) O(\log n \log V) O(lognlogV) 的。
时间复杂度: O ( m log n log V ) O(m \log n \log V) O(mlognlogV) ,可以通过,注意一些细节即可。
#include <bits/stdc++.h>
//using namespace std;using PII = std::pair<int, int>;
using i64 = long long;//线段树模板
template<class Info>
struct Segtree {
#define lson k << 1, l, mid
#define rson k << 1 | 1, mid + 1, rint n;std::vector<Info> info;Segtree(int _n) : n(_n), info((_n + 5) << 2) {};Segtree(std::vector<Info>& arr) : Segtree(arr.size() - 1) {std::function<void(int, int, int)> build = [&](int k, int l, int r) {if (l == r) {info[k] = arr[l];return;}int mid = l + r >> 1;build(lson), build(rson);pushup(k, l, r);};build(1, 1, n);}void pushup(int k, int l, int r) {info[k] = merge(info[k << 1], info[k << 1 | 1], l, r);}void Modify(int k, int l, int r, int x, const Info& z) {if (l == r) return void(info[k] = z);int mid = l + r >> 1;if (x <= mid) Modify(lson, x, z);if (x > mid) Modify(rson, x, z);pushup(k, l, r);}Info Query(int k, int l, int r, int x, int y) {if (l >= x && r <= y) return info[k];int mid = l + r >> 1;if (y <= mid) return Query(lson, x, y);if (x > mid) return Query(rson, x, y);return merge(Query(lson, x, y), Query(rson, x, y), std::max(l, x), std::min(y, r));}void Modify(int pos, const Info& z) {Modify(1, 1, n, pos, z);}Info Query(int l, int r) {return Query(1, 1, n, l, r);}
};int X;//注意这里的信息维护和答案上推操作
struct Info {i64 sum;std::vector<PII> L, R;friend Info merge(const Info& a, const Info& b, int QL, int QR) {Info res;res = { a.sum + b.sum, a.L, b.R };//R即 [l,mid] 的后缀或数组,L即[mid+1,r]的前缀或数组auto& R = a.R, & L = b.L;//这里的不同点是从大到小枚举 [mid+1,r] 的后缀或数组,同时查询 [l,mid] 的前缀或数组是否存在合法答案for (int l = R.size() - 1, r = 0; r < L.size(); ++r) {while (l > 0 && (R[l - 1].first | L[r].first) >= X) {--l;}//当答案满足时注意统计信息if ((R[l].first | L[r].first) >= X) {int Rlen = (r + 1 >= L.size() ? QR + 1 : L[r + 1].second) - L[r].second;int Llen = R[l].second - QL + 1;res.sum += 1LL * Rlen * Llen;}}//同时将维护的信息进行上推//保证[l,mid]的前缀或数组不变,枚举[mid+1,r]的前缀或数组上推 [l,r] 的前缀或数组for (auto& [v, p] : b.L) {auto& [x, _] = res.L.back();if ((x | v) > x) {res.L.emplace_back(x | v, p);}}//同时将维护的信息进行上推//保证[mid+1,r]的后缀或数组不变,枚举[l,mid]的后缀或数组上推 [l,r] 的后缀或数组for (auto& [v, p] : a.R) {auto& [x, _] = res.R.back();if ((x | v) > x) {res.R.emplace_back(x | v, p);}}//返回信息return res;}
};void solve() {int n, q;std::cin >> n >> q >> X;std::vector<Info> A(n + 1);for (int i = 1; i <= n; ++i) {int val;std::cin >> val;A[i].L.emplace_back(val, i);A[i].R.emplace_back(val, i);A[i].sum = (val >= X);}Segtree<Info> S(A);for (int i = 1; i <= q; ++i) {int op, l, r;std::cin >> op >> l >> r;if (op == 1) {S.Modify(l, {(r >= X), {{r, l}}, {{r, l}} });} else {std::cout << S.Query(l, r).sum << "\n";}}
}signed main() {std::ios::sync_with_stdio(0);std::cin.tie(0);int t = 1;//std::cin >> t;while (t--) {solve();}return 0;
}

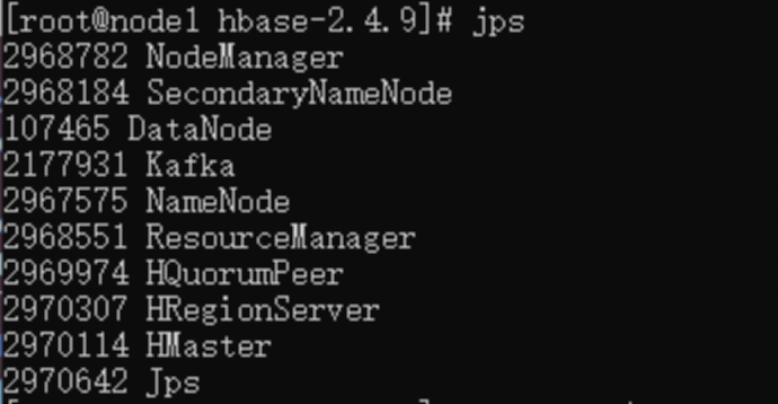







![[000-01-030].第2节 :Zookeeper本地安装](https://i-blog.csdnimg.cn/blog_migrate/89824fcd7b048a4e0a5459ec898028b1.png)