虚假新闻检测
一、项目主题
针对媒体出现的虚假新闻和真实新闻进行检测识别。
动机:在这个社交媒体和互联网的世界中,我们接触到各种新闻和文章,但其中一些新闻和文章是假的,是为了好玩或出于恶意而制作的,这对社会是非常有害的。想对媒体产生的新闻进行鉴别,实现对虚假新闻和真实新闻的检测分类识别,以便用户对获取到的新闻进行清晰的认知,排除虚假新闻对用户的影响。
方法:采用监督学习模式,使用 T f i d f V e c t o r i z e r , C o u n t V e c t o r i z e r , P a s s i v e A g g r e s s i v e C l a s s i f i e r TfidfVectorizer,CountVectorizer,PassiveAggressiveClassifier TfidfVectorizer,CountVectorizer,PassiveAggressiveClassifier ,贝叶斯分类器对文本进行分类。
数据集dataset:https://download.csdn.net/download/weixin_51206814/54260176
代码链接:https://download.csdn.net/download/weixin_51206814/55499702
项目实例:在实验过程中,参考以下论文实例。
- [1]许丽,焦博,赵章瑞.基于TF-IDF的加权朴素贝叶斯新闻文本分类算法[J].网络安全技术与应用,2021(11):31-33.
- [2]陈翠娟.改进的多项朴素贝叶斯分类算法和Python实现[J].景德镇学院学报,2021,36(03):92-95.
二、实验报告
2.1 方法介绍
2.1.1 贝叶斯分类文本
贝叶斯分类算法是一种以统计学为基础的分类算法。朴素贝叶斯分类算法是对传统贝叶斯分类算法进行朴素的假设,所谓朴素就是假设数据类别之间彼此独立,互不产生任何影响。首先要计算属于某一 类的先验概率,然后再利用贝叶斯定理计算其属于此类的后验概率,对各类后验概率的大小进行比较就可进行分类。贝叶斯公式也称为贝叶斯法则,它是关于随机事件 A A A 和 B B B 的条件概率和边缘概率的。任何事件的发生都不是完全偶然的,往往都是以其他事件的发生为基础的。条件概率研究的就是在事件 A A A 发生的基础上,事件 B B B 发生的概率。贝叶斯法则是根据已知先验概率求后验概率。后验概率就是一种条件概率,一般的条件概率是由因求果,后验概率则是知果求因。
在对新闻文本的表示中,使用一个 n n n 维向量的形式在多维空间进行表示,对文本的每个词赋予一个权重,在本实验中采用 T F − I D F TF-IDF TF−IDF 来计算特征词的权重,下一部分将对这个 T F − I D F TF-IDF TF−IDF 进行详细解释。特征权重就是该词对应空间向量的一个维度坐标,可以进行如下表示:
新闻文本 f i f_i fi 在向量空间中就可以表示为:
V ( f i ) = ( W i 1 , W i 2 , ⋯ , W i n ) V(f_i)=(W_{i1},W_{i2},\cdots,W_{in}) V(fi)=(Wi1,Wi2,⋯,Win)
其中, f i f_i fi 是数据集中第 i i i 篇新闻文本, i = 1 , 2 , ⋯ , m ; n i=1,2,\cdots,m;n i=1,2,⋯,m;n 是 f i f_i fi 中含有的特征词个数, W i j W_{ij} Wij 是新闻文本 f i f_i fi 中特征词 t j t_j tj 的特征权重, j = 1 , 2 , ⋯ , n j =1,2,\cdots,n j=1,2,⋯,n。
对于文本分类来说,设训练数据集 F = { f 1 , f 2 , ⋯ , f m } F =\{f_1,f_2,\cdots,f_m\} F={f1,f2,⋯,fm},训练集数据分为 k k k 类,记为 C i , i = 1 , 2 , ⋯ , k C_i,i=1,2,\cdots,k Ci,i=1,2,⋯,k。类 C i C_i Ci 的先验概率为 P ( C i ) P(C_i) P(Ci) ,则文本 d d d 的后验概率为:
P ( C k ∣ d ) = P ( d ∣ C k ) P ( C k ) P ( d ) P(C_k|d) = \frac{P(d|C_k)P(C_k)}{P(d)} P(Ck∣d)=P(d)P(d∣Ck)P(Ck)
有朴素贝叶斯算法的独立性假设:各个特征词之间是相互独立。可以得到条件概率:
P ( d ∣ C k ) = P ( ( W i 1 , W i 2 , ⋯ , W i n ) ∣ C k ) = ∏ i = 1 n P ( W i n ∣ C k ) 代 入 上 式 可 得 : P ( C k ∣ d ) = P ( C k ) ∏ i = 1 n P ( W i n ∣ C k ) P ( d ) P(d|C_k) =P((W_{i1},W_{i2},\cdots,W_{in})|C_k)=\prod_{i=1}^nP(W_{in}|C_k)\\ 代入上式可得:P(C_k|d)=\frac{P(C_k)\prod_{i=1}^n P(W_{in}|C_k)}{P(d)} P(d∣Ck)=P((Wi1,Wi2,⋯,Win)∣Ck)=i=1∏nP(Win∣Ck)代入上式可得:P(Ck∣d)=P(d)P(Ck)∏i=1nP(Win∣Ck)
由于 P ( d ) P(d) P(d) 是确定不变的,因此在比较后验概率的时候只需要比较分子部分即可。即:
C k = a r g max P ( C k ) ∏ i = 1 n P ( W i n ∣ C k ) C_k =arg\ \max P(C_k)\prod_{i=1}^nP(W_{in}|C_k) Ck=arg maxP(Ck)i=1∏nP(Win∣Ck)
在 P ( W i n ∣ C k ) P(W_{in}|C_k) P(Win∣Ck) 中,实际可以将其看作是 T F − I D F TF-IDF TF−IDF 的值,用 T F − I D F TF-IDF TF−IDF 的值代替概率进行计算。(个人理解)
2.1.2 采用TF-IDF文本特征提取
T F TF TF 指词频,表示某个词在文章中出现的频次; I D F IDF IDF 指逆文档频率,表示包含该词的文档数占语料库文档数的比例。
词 频 ( T F ) = 某 词 出 现 在 文 章 中 的 次 数 逆 文 档 频 率 ( I D F ) = l o g ( 语 料 库 文 档 总 数 + 1 包 含 该 词 的 文 档 数 + 1 ) + 1 T F − I D F = T F × I D F 词频(TF) = 某词出现在文章中的次数 \\ 逆文档频率(IDF) =log(\frac{语料库文档总数+1}{包含该词的文档数+1})+1\\ TF-IDF = TF \times IDF 词频(TF)=某词出现在文章中的次数逆文档频率(IDF)=log(包含该词的文档数+1语料库文档总数+1)+1TF−IDF=TF×IDF
对于不单独使用词频是由于一些普遍出现的词,在文章出现的次数一般也越高,那么词频就会较高,从词频角度分析,看起来似乎是更重要的特征,但因为这个词普遍出现,这个词可能不是非常的重要,那么单独采用词频 ( T F ) (TF) (TF) 进行向量化特征表示就无法反应这一点。
使用 T F − I D F TF-IDF TF−IDF 的基本思想:如果某个词语在某篇文档中出现的频率很高,从 T F TF TF 的角度来说就是, T F TF TF 很高,但是在语料库内的其他文档中出现的频率很低,从 I D F IDF IDF 角度来说,就是 I D F IDF IDF 高,则认定此词语在某种程度上可作为该文档的特征词,具备类别区分能力,可作为分类的依据。一个字词的重要性与它在某份文件中出现的次数正相关,字词在文件中出现的次数越多重要性越大,但同时与它在语料库中出现的频率呈负相关,语料库中出现的次数越多,则该字词的重要性越小。
在对文本特征提取的过程中,可以采用 T f i d f V e c t o r i z e r TfidfVectorizer TfidfVectorizer 或者 C o u n t V e c t o r i z e r CountVectorizer CountVectorizer ,两种方法区别不大,本实验主要采用 T f i d f V e c t o r i z e r TfidfVectorizer TfidfVectorizer ,下面介绍一下在使用 T f i d f V e c t o r i z e r TfidfVectorizer TfidfVectorizer 对文本特征进行提取的过程。
-
使用 T f i d f V e c t o r i z e r TfidfVectorizer TfidfVectorizer 需要调用机器学习 s k l e a r n sklearn sklearn 的库,下面是调库语句。
from sklearn.feature_extraction.text import TfidfVectorizer -
定义语料库的语句,为了便于观察原理过程,语料库加入了两个句子。
corpus=["I come to China to travel", "This is a car polupar in China"] -
定义完语料库后,调用 T f i d f V e c t o r i z e r TfidfVectorizer TfidfVectorizer ,出于数据集是英文文本,设置停用词 “ e n g l i s h english english”,将包含在 n l t k . c o r p u s nltk.corpus nltk.corpus 的英语停止词中的单词进行删除,这些词包括介词、连词、冠词、to be 等没有意义的词。对语料库根据 T f i d f V e c t o r i z e r TfidfVectorizer TfidfVectorizer 参数规则进行操作,比如滤除停用词等,拟合原始数据,生成文档中有价值的词汇表,结合 f i t _ t r a n f o r m fit\_tranform fit_tranform 完成向量化。

上图是滤除停用词后的结果,可以看见将语料库中的一些冠词、连词等删除,同时对这些词语按字母序排序,得到一个 “ v o c a b u l a r y vocabulary vocabulary” ,得到这个后,对语料库里的句子文本进行处理,结合 f i t _ t r a n f o r m fit\_tranform fit_tranform 对词语进行向量化。结果如下:
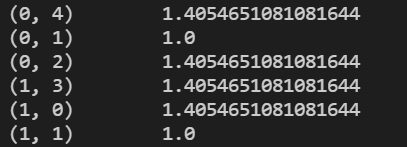
上图 ( 0 , 4 ) (0,4) (0,4) 表示第 0 0 0 个字符串,词汇表里第 4 4 4 个单词的 T F − I D F TF-IDF TF−IDF 值。计算过程为:单词 t r a v e l travel travel 在第 0 0 0 个字符串也就是语料库的第一个句子中,词频为 T F = 1 TF=1 TF=1 ,逆文档频率 I D F = l o g 2 + 1 1 + 1 + 1 = l o g 3 2 + 1 = 1.40546108 IDF = log\frac{2+1}{1+1}+1 = log\frac{3}{2}+1=1.40546108 IDF=log1+12+1+1=log23+1=1.40546108, T F − I D F = T F × I D F = 1 × 1.40546 = 1.40546108 TF-IDF=TF\times IDF=1\times 1.40546 = 1.40546108 TF−IDF=TF×IDF=1×1.40546=1.40546108。其他单词同理。
结合 t o a r r a y ( ) toarray() toarray() 转成数据矩阵形式进行显示,这个矩阵是一个稀疏矩阵,如图, ( 0 , 0 ) (0,0) (0,0)位置的值为 0 0 0 ,解释为第 0 0 0 个字符串,词汇表里第 0 0 0 个单词,也就是 c a r car car,实际中根本没有在语料库第一句中出现,因此值为 0 0 0。由于当文本量庞大的时候,矩阵将会变得十分巨大,不利于显示,因此后续不做输出。

下面是实现上述过程的示例代码。tv_fit = tv.fit_transform(corpus) tv.get_feature_names_out()#生成提取的文本滤除停用词后的单词 print("tv.get_feature_names_out") print(tv.get_feature_names_out())#将单词输出 # print("tv.vocabulary") dict = tv.vocabulary_#生成词汇表 print(dict)#输出词汇表 print("tv_fit") print(tv_fit)#输出向量化后的结果 re = tv_fit.toarray() print(re)#输出转矩阵后的结果
2.1.3 PassiveAggressiveClassifier 分类模型
P a s s i v e A g g r e s s i v e Passive\ Aggressive Passive Aggressive,是经典的 o n l i n e online online 线性分类器,它可以不断的整合新样本去调整分类模型,增强模型的分类能力。这样的模型在处理数据量庞大的数据集时,能够解决对数据读取时占用大量内存,使内存受限的情况,避免内存占用过大,解决内存问题。
P a s s i v e A g g r e s s i v e C l a s s i f i e r Passive\ Aggressive\ Classifier Passive Aggressive Classifier 的具体实现和参考算法。(可以参考 https://blog.csdn.net/weixin_38493025/article/details/80728688 )
算法伪代码:
I n p u t : a g g r e s s i v e n e s s p a r a m e t e r C > 0 Input: aggressiveness\ parameter\ C > 0 Input:aggressiveness parameter C>0
I n i t i a l i z e : W = ( 0 , 0 , ⋯ , 0 ) Initialize: W = (0,0,\cdots ,0) Initialize:W=(0,0,⋯,0)
F o r t = 1 , 2 , ⋯ For \ t =1,2,\cdots For t=1,2,⋯
-
r e c i v e i n s t a n c e : X t ∈ R recive \ instance : X_t \in R recive instance:Xt∈R
-
p r e d i c t c o r r e c t l a b e l : y t ∈ { − 1 , + 1 } predict\ correct \ label :y_t\in\{-1,+1\} predict correct label:yt∈{−1,+1}
-
s u f f e r l o s s : ℓ t = max { 0 , 1 − y t ( W t ⋅ X t ) } suffer \ loss : \ell_t=\max\{0,1-y_t(W_t\cdot X_t)\} suffer loss:ℓt=max{0,1−yt(Wt⋅Xt)}
-
u p d a t e update update
-
1. s e t 1. \ set 1. set
τ t = ℓ t ∣ ∣ X t ∣ ∣ 2 τ t = min { C , ℓ t ∣ ∣ X t ∣ ∣ 2 } τ t = ℓ t ∣ ∣ X t ∣ ∣ 2 + 1 2 C \tau_t = \frac{\ell_t}{||X_t||^2} \\ \tau_t = \min\{C,\frac{\ell_t}{||X_t||^2}\} \\ \tau_t = \frac{\ell_t}{||X_t||^2+\frac{1}{2C}} τt=∣∣Xt∣∣2ℓtτt=min{C,∣∣Xt∣∣2ℓt}τt=∣∣Xt∣∣2+2C1ℓt -
2. u p d a t e 2.\ update 2. update
W t + 1 = W t + τ t y t X t W_{t+1} = W_t+\tau_t y_t X_t Wt+1=Wt+τtytXt
-
2.2 实验设计
2.2.1 数据处理
对数据集进行读取,并且对数据集的列表数和个数进行统计,输出数据集中的前五行数据进行展示。![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qtDbKcc1-1638544404355)(C:\Users\laiping\AppData\Roaming\Typora\typora-user-images\image-20211202163342090.png)]](https://img-blog.csdnimg.cn/8f78e71175d94063b5bd6e5b9324b9a4.png)
观察数据可以看见,有 4 4 4 列数据共 6335 6335 6335 条,标签 l a b e l label label 分为 “ F A K E FAKE FAKE” 和 “ R E A L REAL REAL” 两类,获取标签。然后对数据集进行分割,分割为训练集和测试集,采用对 “ t e x t text text” 和 “ l a b e l label label” 列数据进行分割,分割的测试集大小为 0.2 0.2 0.2, r a n d o m _ s t a t e random\_state random_state 是随机数种子,设置的数字相同能保证每次拆分的数据集是一样的。
x_train,x_test,y_train,y_test=train_test_split(df['text'], labels, test_size=0.2, random_state=12)
对数据集进行分类后,对 “ t i t l e title title” 内容进行文本特征提取,采取 T f i d f V e c t o r i z e r TfidfVectorizer TfidfVectorizer 或者 C o u n t V e c t o r i z e r CountVectorizer CountVectorizer 建立特征权重。拟合和变换训练集,变换测试集,建立数据特征矩阵。使用" f i t _ t r a n s f o r m fit\_transform fit_transform" 加载数据并将数据转化为数据矩阵形式。
# TfidfVectorizer 形式
# tfidf_vectorizer = TfidfVectorizer(analyzer = 'word',stop_words = 'english',norm = None)
# CountVectorizer 形式
tfidf_vectorizer = CountVectorizer()
tfidf_train=tfidf_vectorizer.fit_transform(x_train)
tfidf_test=tfidf_vectorizer.transform(x_test)



上图为生成的词汇表和特征向量化、矩阵的结果。
2.2.2 调用模型
了解到有两种模型可供使用对于新闻文本分类,两种分类模型都能避免内存爆炸的情况出现,两种模型都能不断的整合新数据调整分类模型,能达到提高分类能力的结果。
2.2.2.1 PassiveAggressiveClassifier 分类模型
调用机器学习 “ s k l e a r n sklearn sklearn” 里的 “ l i n e a r _ m o d e l linear\_model linear_model” 里的 “ P a s s i v e A g g r e s s i v e C l a s s i f i e r PassiveAggressiveClassifier PassiveAggressiveClassifier” 分类模型,设置参数 m a x _ i t e r max\_iter max_iter ,可以调整迭代次数观察对于最后准确率的影响(迭代次数设置越大,分类准确率越大)。
#max_iter 迭代次数越大,分类准确率就越大
pac = PassiveAggressiveClassifier(max_iter=50)
2.2.2.2 贝叶斯分类模型对文本进行分类
贝叶斯分类模型分为三种, G a u s s i a n N B GaussianNB GaussianNB 就是先验为高斯分布的朴素贝叶斯, M u l t i n o m i a l N B MultinomialNB MultinomialNB 就是先验为多项式分布的朴素贝叶斯, B e r n o u l l i N B BernoulliNB BernoulliNB 就是先验为伯努利分布的朴素贝叶斯。
-
G a u s s i a n N B GaussianNB GaussianNB 贝叶斯
-
pac = GaussianNB() #由于TF-IDF得到的是稀疏矩阵,使用todense变得密集 tfidf_train = tfidf_train.todense() tfidf_test = tfidf_test.todense()
-
-
M u l t i n o m i a l N B MultinomialNB MultinomialNB 贝叶斯
-
pac = MultinomialNB()
-
-
B e r n o u l l i N B BernoulliNB BernoulliNB 贝叶斯
-
pac = BernoulliNB()
-
这是贝叶斯三种模型的调用代码,分别调用完模型后,进行模型训练。
pac.fit(tfidf_train,y_train)
2.2.2.3 使用模型进行预测
在调用模型对训练集进行训练过后,需要对测试集进行预测,然后将实际结果与预测结果进行对比。
y_pred=pac.predict(tfidf_test)#预测测试集
#print(y_pred)
#print(y_test)
在数据量小的时候,可以将测试集的实际结果与预测结果进行输出观察预测情况对比。
完成预测后,比较测试集实际结果,计算正确率和混淆矩阵并对结果进行分析。
2.3 结果与分析
2.3.1 准确率对比
-
P a s s i v e A g g r e s s i v e C l a s s i f i e r PassiveAggressiveClassifier PassiveAggressiveClassifier 分类模型
采用 T f i d f V e c t o r i z e r TfidfVectorizer TfidfVectorizer 的情况,调整 t e s t _ s i z e test\_size test_size 、 r a n d o m _ s t a t e random\_state random_state、 m a x _ i t e r max\_iter max_iter 三个参数比较最后分类正确率。
n u m b e r number number t e s t _ s i z e test\_size test_size r a n d o m _ s t a t e random\_state random_state m a x _ i t e r max\_iter max_iter a c c u r a c y accuracy accuracy 1 0.2 7 50 91.32% 2 0.3 7 50 90.22% 3 0.4 7 50 89.94% 4 0.2 12 50 90.45% 5 0.2 20 50 92.19% 6 0.2 30 50 90.84% 7 0.2 7 100 91.55% 8 0.2 7 150 91.79% 9 0.2 7 200 91.63% 分析上表格可以看出,在训练集较少的情况下对测试集进行测试,可能会得到不太好的预测结果,另外 r a n d o m _ s t a t e random\_state random_state、 m a x _ i t e r max\_iter max_iter 两个参数从上表来看对结果的影响并无太大关系,但从实际分析,迭代次数会影响分类效果。
绘出准确率与迭代次数之间的折线图。观察下图可以看出迭代次数会影响分类效果。

-
贝叶斯模型
-
G a u s s i a n N B GaussianNB GaussianNB 贝叶斯
n u m b e r number number t e s t _ s i z e test\_size test_size a c c u r a c y accuracy accuracy 1 0.2 80.98% 2 0.3 79.22% 3 0.4 79.95% -
M u l t i n o m i a l N B MultinomialNB MultinomialNB 贝叶斯
n u m b e r number number t e s t _ s i z e test\_size test_size a c c u r a c y accuracy accuracy 1 0.2 90.13% 2 0.3 89.37% 3 0.4 88.6% -
B e r n o u l l i N B BernoulliNB BernoulliNB 贝叶斯
n u m b e r number number t e s t _ s i z e test\_size test_size a c c u r a c y accuracy accuracy 1 0.2 82.08% 2 0.3 82.22% 3 0.4 82.56%
-
从上述三种模型分类的结果分析,采用 M u l t i n o m i a l N B MultinomialNB MultinomialNB 多项式贝叶斯分类的准确率最高,主要跟先验概率的分布有关系。
通过上述四种模型准确率对比,绘出四种模型准确率柱状图,可以清晰看出四种模型的差异。 
2.3.2 混淆矩阵
在结果的部分,采用混淆矩阵的形式对模型预测结果进行可视化以及结果呈现。
混淆矩阵( c o n f u s i o n m a t r i x confusion\ matrix confusion matrix),又称为可能性表格或是错误矩阵。它是一种特定的矩阵用来呈现算法性能的可视化效果,通常是监督学习,其每一列代表预测值,每一行代表的是实际的类别。这个名字来源于它可以非常容易的表明多个类别是否有混淆(也就是一个 c l a s s class class 被预测成另一个 c l a s s class class)。
在预测分析中,混淆表格(有时候也称为混淆矩阵),是由 f a l s e p o s i t i v e s false \ positives false positives, f a l s e n e g a t i v e s false\ negatives false negatives, t r u e p o s i t i v e s true \ positives true positives 和 t r u e n e g a t i v e s true \ negatives true negatives 组成的两行两列的表格。它允许我们做出更多的分析,而不仅仅是局限在正确率。准确率对于分类器的性能分析来说,并不是一个很好地衡量指标,因为如果数据集不平衡(每一类的数据样本数量相差太大),很可能会出现误导性的结果。
在二分类的模型中,混淆矩阵把预测情况与实际情况的所有结果进行组合,形成了真正 ( t r u e p o s i t i v e ) (true \ positive) (true positive)、假正 ( f a l s e p o s i t i v e ) (false\ positive) (false positive)、真负 ( t r u e n e g a t i v e ) (true \ negative) (true negative) 和假负 ( f a l s e n e g a t i v e ) (false\ negative) (false negative) 四种情形,分别由 T P 、 F P 、 T N 、 F N TP、FP、TN、FN TP、FP、TN、FN 表示( T T T 代表预测正确, F F F 代表预测错误)。
- P a s s i v e A g g r e s s i v e C l a s s i f i e r PassiveAggressiveClassifier PassiveAggressiveClassifier 分类模型的混淆矩阵

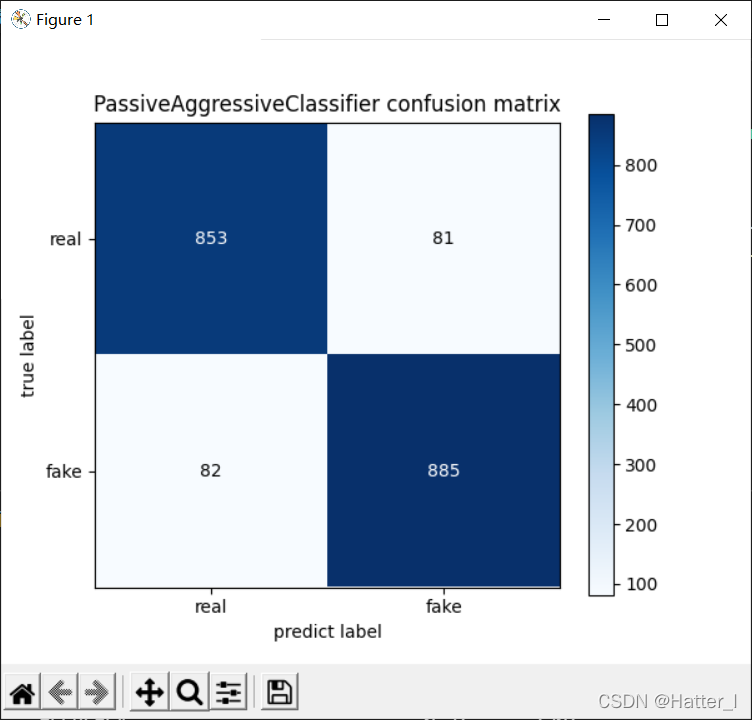
- M u l t i n o m i a l N B MultinomialNB MultinomialNB贝叶斯分类模型的混淆矩阵
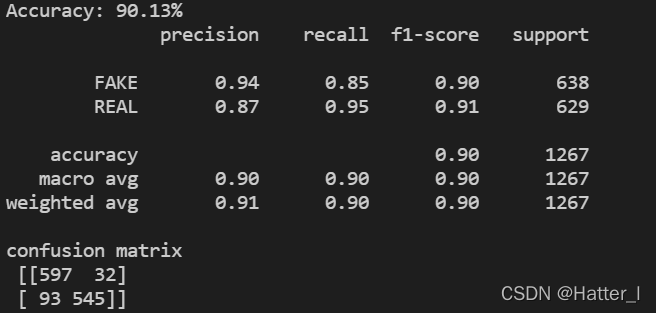
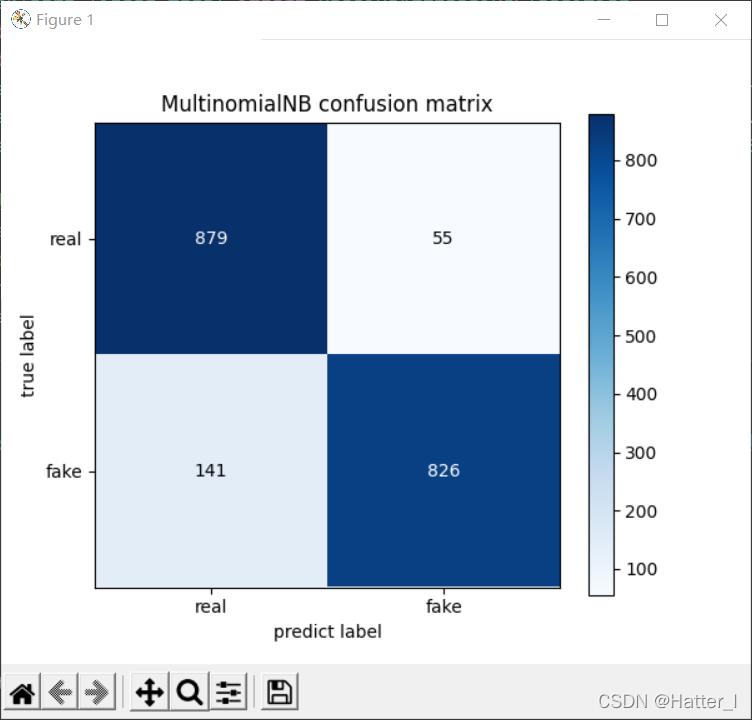
2.3.3 分析
使用贝叶斯模型的优点:
- 在于能够使用较小的空间获得更好的算法效率,空间开销小,具有稳定的分类效率,占用比较小的空间内存量,并且对缺失数据不太敏感。
使用贝叶斯模型的缺点:
- 需要提前知道先验概率,同时贝叶斯的假设是每个特征属性是独立,因此在属性有关联时就会使分类效果不好。