问题描述

给定一个数组，它的第 $i$ 个元素为一支给定的股票在第 $i$ 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 $k$ 笔交易。

注意：你不能同时参与多笔交易，你必须在再次购买前出售掉之前的股票。

示例 1:

输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2:

输入: [3,2,6,5,0,3], k = 2
输出: 7
解释: 在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

解析

这道题可以用动态规划的思想来解决。
每到新的一天，有三种选择：购买股票（在没有持有股票的情况下），不买也不卖，卖出手中的股票（在持有股票的前提下）。同一天不能既卖出股票又买入股票。

此外，还有购买次数 $k$ 的限制，在超出购买次数后，只能在持有股票的前提下，将手中的股票卖出，或者继续观望。

按照上述规律我们可以定义：
状态方程 $dp[i][k][0]$ 的含义为：在第 $i$ 天中，已经消耗了 $k$ 次股票购买机会，并且没有持有股票。
状态方程 $dp[i][k][1]$ 的含义为：在第 $i$ 天中，已经消耗了 $k$ 次股票购买机会，并且当前持有股票。
例如$dp[2][1][0]$ 的含义就是在第2天中，已经消耗了1次股票购买机会，并且当前没有持有股票。

状态方程$dp[i][k][0]$ 或者 $dp[i][k][1]$ 的值定义为当前的收益（可以为正也可以为负），当购买股票时，需要减去$prices[i]$，抛售股票时需要加上 $prices[i]$。可以看出，题目的最优解为 $max(dp[i][0][0],dp[i][1][0],...,dp[i][k][0])$，因为我们并不需要一定把购买机会 $k$ 用完。

可以总结出状态转移方程：
$dp[i][k][0]=max(dp[i-1][k][0],dp[i-1][k][1]+prices[i])$
解释：$dp[i][k][0]$ 代表今天我没有持有股票，那么也就有两种可能性，第一种可能性是昨天没买也没有持有股票。第二种可能性是昨天已经持有了股票，然后今天将股票抛售出去（这里定义抛售不会改变 $k$ 的值，只有购买才会将 $k$ 的值加上1）。

$dp[i][k][1]=max(dp[i-1][k][1],dp[i-1][k-1][0]-prices[i])$
解释：$dp[i][k][1]$ 代表今天我持有股票，也有两种可能性：第一种是昨天就已经持有了股票。第二种可能性就是昨天没有持有股票，然后今天我购买了这笔股票，所以要减去 $prices[i]$。

状态转移方程定义好后，我们需要定义好初始状态，也就是第一天的所有状态：

• $dp[0][0][0]=0$，含义是第1天不买任何股票。
• $dp[0][1][1]=-price[0]$，含义是第1天买下当天的股票。
• 第1天除去上述两个状态以外的所有状态都赋值为 $-\infty$（因为第一天只有上述两种可能），在代码中可以表示为Integer.MIN_VALUE >> 1，这里除以2是为了防止在减法运算时超出范围变为正数

计算初始状态的代码为：

for (int i = 0; i <= k; i++) {dp[0][i][0] = Integer.MIN_VALUE >> 1;dp[0][i][1] = Integer.MIN_VALUE >> 1;
}dp[0][0][0] = 0;
dp[0][1][1] = -prices[0];

接下来就是计算状态，根据状态转移方程可以看出，每天的状态都依赖于前一天的状态，所以可以通过两层循环，外层循环从第2天开始遍历（因为第一天的状态已经定义好），然后内层循环从 1 遍历到 $k$：

for(int i = 1; i < day; i++) {for(int j = 1; j <= k; k++) {dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);}
}

为什么不计算 $j=0$ 的状态呢，因为$j=0$ 的状态意味着没有购买也没有售出任何一支股票，自然也就等于0了，而在Java语言中，数组初始化后初始值为0，此外当$j=0$时 $dp[i][j][1]$ 这种不可能的状态也没必要计算，因为在上述代码中$dp[i][j][1]$只依赖于$dp[i-1][j-1][0]$。

完成上述状态的计算后，最后就是求 $max(dp[i][0][0],dp[i][1][0],...,dp[i][k][0])$ 也就是题目的答案了。

int ans = 0;
for (int i = 0; i <= k; i++) {ans = Math.max(ans, dp[day - 1][i][0]);
}

分析完成后，我们来看看如何利用上述方程解6道关于股票买卖问题的LeetCode算法题。

---

LeetCode 121：买卖股票的最佳时机

给定一个数组，它的第 $i$ 个元素是一支给定股票第 $i$ 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

示例 2:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

分析

这道题实际上就是上述原型中的 $k=1$ 的例子。也可以直接套在上述解题模板中，但是之前我们提到过，$k=0$ 的状态意味着没有购买也没有售出任何一支股票，所以恒为0，所以在本题中原先的状态转移方程可以改写为：

$dp[i][k][0]=max(dp[i-1][k][0],dp[i-1][k][1]+prices[i])$
$dp[i][k][1]=max(dp[i-1][k][1],-prices[i])$

可以看出，因为$dp[0][0][0],dp[1][0][0],...,dp[n][0][0]=0$，并且也只有$dp[i][k][1]$依赖于$k$的前一个状态 $dp[i][k-1][0]$，而 $k$ 的最大值为1，所以 $dp[i][k-1][0]=0$，也就可以省略$dp[i][k-1][0]$ 了，也就变成了$-prices[i]$。

上述状态转移方程还可以简化，就是去除状态 $k$，因为上述状态转移方程中 $k$ 已经不依赖于$k-1$了，所以该维度可以除去，最终变为：

$dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i])$
$dp[i][1]=max(dp[i-1][1],-prices[i])$

题目最后的答案为：

class Solution {public int maxProfit(int[] prices) {int len = prices.length;if(len == 0) {return 0;}int[][] dp = new int[len][2];dp[0][0] = 0;dp[0][1] = -prices[0];for (int i = 1; i < len; i++) {dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);}return dp[len - 1][0];}
}

其时间复杂度为 $O(n)$，空间复杂度为$O(n)$。

当然这道题由于情况比较简单，还有更省空间、快速的解法。因为只能购买一次，所以我们只需要找出第 $i$ 天之后的最大值就可以了，也就是找到数组price的i + 1 ~ len的最大值。我们定义 $dp[i]$ 为数组price的i + 1 ~ len的最大值，可以得到 $dp[i]$ 的状态转移方程为：

$dp[i]=max(dp[i+1],prices[i])$

显然我们只需要找出$dp[i]-prices[i]$的最大值就可以了，也就是

$max(dp[0]-prices[0],dp[1]-prices[1],...,dp[n]-prices[n])$

最终代码：

class Solution {public int maxProfit(int[] prices) {int len = prices.length;if(len == 0) {return 0;}int[] dp = new int[len];dp[len - 1] = prices[len - 1];for (int i = len - 2; i >= 0; i--) {dp[i] = Math.max(dp[i + 1], prices[i]);}int max = 0;for (int i = 0; i < len - 1; i++) {max = Math.max(dp[i] - prices[i], max);}return max;}
}

其时间复杂度为$O(n)$，空间复杂度为 $O(n)$。

LeetCode 122：买卖股票的最佳时机II

给定一个数组，它的第 $i$ 个元素是一支给定股票第 $i$ 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0

分析

这种是属于$k=+\infty$ 的情况，因为 $+\infty$ 无论加1减去1都等于 $+\infty$，可以认定 $k$ 和 $k-1$ 是等价的，可以根据这个推导出状态转移方程：

$dp[i][k][0]=max(dp[i-1][k][0],dp[i-1][k][1]+prices[i])$
$dp[i][k][1]=max(dp[i-1][k][1],dp[i][k-1][0]-prices[i])=max(dp[i-1][k][1],dp[i][k][0]-prices[i])$

上述状态转移方程中 $k$ 已经不依赖于$k-1$了，所以 $k$ 这个维度可以去除，变为：

$dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i])$
$dp[i][1]=max(dp[i-1][1],dp[i][0]-prices[i])$

最终代码：

class Solution {public int maxProfit(int[] prices) {int len = prices.length;if(len == 0) {return 0;}int[][] dp = new int[len][2];dp[0][0] = 0;dp[0][1] = -prices[0];for (int i = 1; i < len; i++) {dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);dp[i][1] = Math.max(dp[i - 1][1], dp[i][0] - prices[i]);}return dp[len - 1][0];}
}

相比第一个，也就只有dp[i][1] = Math.max(dp[i - 1][1], dp[i][0] - prices[i])这一行发生了改变。时间复杂度为$O(n)$，空间复杂度为$O(n)$。

此外，还有更快速更省空间的解法，也就是找出prices数组所有递增子区间，并将所有上升子空间中的最大值和最小值相减的值累加起来，这个和就是该问题的解：

class Solution {public int maxProfit(int[] prices) {int len = prices.length;if(len == 0) {return 0;}int st = 0;  //子区间开始段boolean flag = false;int ans = 0;for (int i = 1; i < len; i++) {if(prices[i] > prices[i - 1]) {if(!flag) {flag = true;st = i - 1; //标记开始段}continue;}if(flag) {ans += prices[i - 1] - prices[st];flag = false;}}if(flag) {ans += prices[len - 1] - prices[st];}return ans;}
}

该算法时间复杂度为 $O(n)$，空间复杂度为 $O(1)$。

LeetCode 123：买卖股票的最佳时机III

给定一个数组，它的第 $i$ 个元素是一支给定的股票在第 $i$ 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: [3,3,5,0,0,3,1,4]
输出: 6
解释: 在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

示例 2:

输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:

输入: [7,6,4,3,1]
输出: 0
解释: 在这个情况下, 没有交易完成, 所以最大利润为 0。

分析

$k=2$ 的情况，按照最开始的解题模板即可：

import static java.lang.Math.*;
class Solution {public int maxProfit(int[] prices) {int len = prices.length;if(len == 0) {return 0;}int[][][] dp = new int[len][3][2];dp[0][0][0] = 0;dp[0][0][1] = Integer.MIN_VALUE >> 1;dp[0][1][1] = -prices[0];dp[0][1][0] = Integer.MIN_VALUE >> 1;dp[0][2][0] = Integer.MIN_VALUE >> 1;dp[0][2][1] = Integer.MIN_VALUE >> 1;for (int i = 1; i < len; i++) {for (int k = 2; k >= 1; k--) {dp[i][k][0] = max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i]);dp[i][k][1] = max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i]);}}return max(dp[len - 1][0][0], max(dp[len - 1][2][0], dp[len - 1][1][0]));}
}

LeetCode 188：买卖股票的最佳时机IV

给定一个数组，它的第 $i$ 个元素是一支给定的股票在第 $i$ 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 $k$ 笔交易。
注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2:

输入: [3,2,6,5,0,3], k = 2
输出: 7
解释: 在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

分析

跟最上面解题模板一模一样，只不过要考虑 $k$ 大于天数的情况。$k$ 大于天数时，把$k$当成正无穷处理，防止内存超限，也就是和买卖股票的最佳时机II的解法一模一样。当$k$ 小于天数时，按照解题模板处理

class Solution {public int maxProfit(int k, int[] prices) {int len = prices.length;if(len == 0 || k == 0) {return 0;} else if(k > len) {return solve2(prices);  //当k大于天数时，当成k为正无穷判断，防止内存超限。}int[][][] dp = new int[len][k + 1][2];for (int t = 0; t <= k; t++) {dp[0][t][0] = Integer.MIN_VALUE >> 1;dp[0][t][1] = Integer.MIN_VALUE >> 1;}dp[0][0][0] = 0;dp[0][1][1] = -prices[0];for (int i = 1; i < len; i++) {for (int t = k; t >= 1; t--) {dp[i][t][0] = Math.max(dp[i - 1][t][0], dp[i - 1][t][1] + prices[i]);dp[i][t][1] = Math.max(dp[i - 1][t][1], dp[i - 1][t - 1][0] - prices[i]);}}int ans = 0;for (int i = 0; i <= k; i++) {ans = Math.max(ans, dp[len - 1][i][0]);}return ans;}private int solve2(int[] prices) {int len = prices.length;int[][] dp = new int[len][2];dp[0][0] = 0;dp[0][1] = -prices[0];for (int i = 1; i < len; i++) {dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);}return dp[len - 1][0];}
}

---

LeetCode 309：最佳买卖股票时机含冷冻期

给定一个整数数组，其中第 $i$ 个元素代表了第 $i$ 天的股票价格 。​
设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

示例:

输入: [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

分析

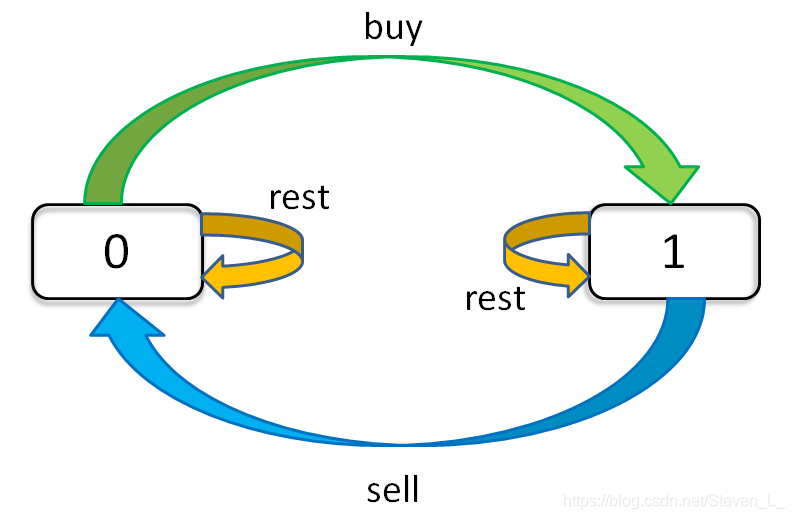
这道题同样是 $k=+\infty$ 的情况，只不过加入了一个冷冻期的概念：当股票被售出后，只有到第三天才能购买。这意味当天的状态从原先的两种：持有股票、未持有股票变成了三种：持有股票、未持有股票、冷冻期。这几种状态的转移情况为：

所以我们将数组 $dp$ 第三维度长度从2扩大到3，来表示当天的第三种状态。根据上述状态机示例图，我们可以推导出以下状态转移方程：

$dp[i][0]=max(dp[i-1][0],dp[i-1][2])$，前者对应由“未持股”->“什么也不做”，后者对应"冷冻期"->“什么也不做”
$dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i])$，前者对应由“持股”->“什么也不做”，后者对应"未持股"->“买入”
$dp[i][2]=dp[i-1][1]+prices[i]$，只有"持股"->"卖出"才能进入冷冻期这个状态。

最后的答案是 $max(dp[n][0],dp[n][2])$。

代码如下：

class Solution {public int maxProfit(int[] prices) {int len = prices.length;if(len == 0) {return 0;}int[][] dp = new int[len][3];dp[0][0] = 0;dp[0][1] = -prices[0];dp[0][2] = Integer.MIN_VALUE >> 1;  //不可能一开始就是冷冻期for (int i = 1; i < len; i++) {dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][2]);dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);dp[i][2] = dp[i - 1][1] + prices[i];}return Math.max(dp[len - 1][0], dp[len - 1][2]);}
}

LeetCode 714：买卖股票的最佳时机含手续费

给定一个整数数组 $prices$，其中第 $i$ 个元素代表了第 $i$ 天的股票价格 ；非负整数 $fee$ 代表了交易股票的手续费用。
你可以无限次地完成交易，但是你每次交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

示例 1:

输入: prices = [1, 3, 2, 8, 4, 9], fee = 2
输出: 8
解释: 能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

注意:

$0<prices.length<=50000.$
$0<prices[i]<50000$
$0<=fee<50000$

分析

$k=+\infty$ 的情况，只不过每次购买时都需要加上手续费，状态转移方程：

$dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]-fee)$
$dp[i][1]=max(dp[i-1][1],dp[i][0]-prices[i])$

代码：

class Solution {public int maxProfit(int[] prices, int fee) {int len = prices.length;if(len == 0) {return 0;}int[][] dp = new int[len][2];dp[0][0] = 0;dp[0][1] = -prices[0];for (int i = 1; i < len; i++) {dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);dp[i][1] = Math.max(dp[i - 1][1], dp[i][0] - prices[i]);}return dp[len - 1][0];}
}