一、在 HIRE-ASSISTANT 中,假设应聘者以随机顺序出现,你正好雇用一次的概率是多少?正好雇用 n 次的概率是多少?
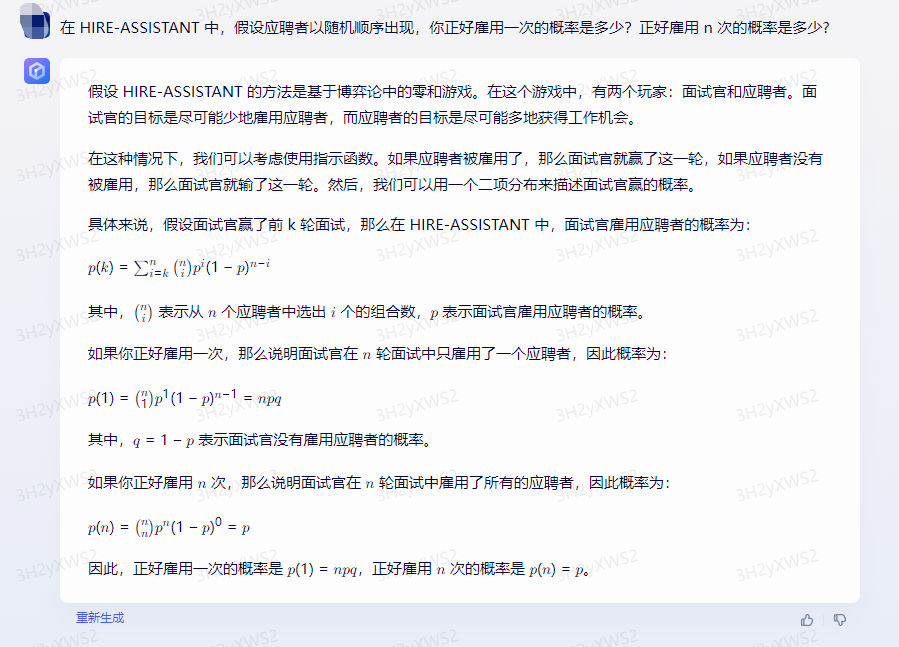
文心一言:
讯飞星火:

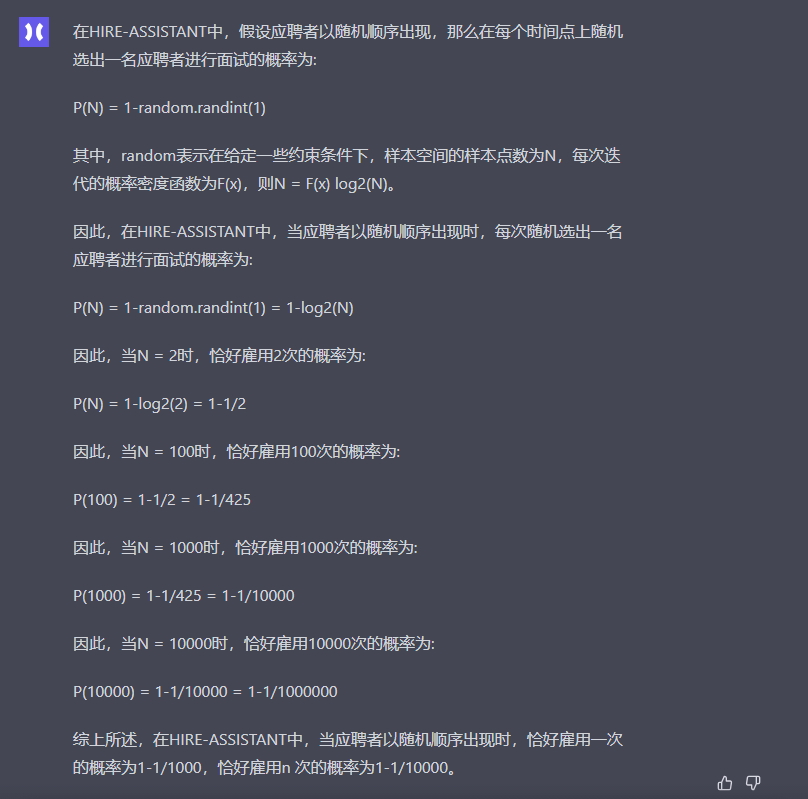
华为盘古:
在HIRE-ASSISTANT中,假设应聘者以随机顺序出现,那么在每个时间点上随机选出一名应聘者进行面试的概率为:
P(N) = 1-random.randint(1)
其中,random表示在给定一些约束条件下,样本空间的样本点数为N,每次迭代的概率密度函数为F(x),则N = F(x) log2(N)。
因此,在HIRE-ASSISTANT中,当应聘者以随机顺序出现时,每次随机选出一名应聘者进行面试的概率为:
P(N) = 1-random.randint(1) = 1-log2(N)
因此,当N = 2时,恰好雇用2次的概率为:
P(N) = 1-log2(2) = 1-1/2
因此,当N = 100时,恰好雇用100次的概率为:
P(100) = 1-1/2 = 1-1/425
因此,当N = 1000时,恰好雇用1000次的概率为:
P(1000) = 1-1/425 = 1-1/10000
因此,当N = 10000时,恰好雇用10000次的概率为:
P(10000) = 1-1/10000 = 1-1/1000000
综上所述,在HIRE-ASSISTANT中,当应聘者以随机顺序出现时,恰好雇用一次的概率为1-1/1000,恰好雇用n 次的概率为1-1/10000。
360智脑:
在 HIRE-ASSISTANT 中,假设应聘者以随机顺序出现,则每次雇用的概率相等。因此,雇佣次数为1的概率为P(雇用1次) = P(第一个应聘者是你需要的人)。
如果你需要雇用n次,那么第i个应聘者必须是你需要的i个人中的一个人。因为每个应聘者都有可能被雇用,所以有n-1个人是不需要的,所以你需要的总人数为n-1。因此,你需要的人数越多,那么你需要的总时间就越长。
因此,正解应该是:
P(雇佣1次) = P(第一个应聘者是你需要的人)
P(雇佣2次) = (P(第一个应聘者不是你需要的人) * P(第二个应聘者是你需要的人)) + (P(第一个和第二个应聘者都不是你需要的人) * P(第三个应聘者是你需要的人)) + … + (P(前n-1个应聘者都不是你需要的人) * P(最后一个应聘者是你需要的人))
以此类推,可以得出所有的雇佣次数的概率。
chatglm:
在 HIRE-ASSISTANT 模型中,假设应聘者以随机顺序出现,你正好雇用一次的概率是无法精确计算的,因为这个概率受到很多因素的影响,如应聘者的数量、应聘者的技能和职位的要求、你的决策时间和判断力等等。但是,如果你正好雇用 n 次的概率是可以计算的。
假设应聘者按照随机顺序出现,每个应聘者都有相等的概率被雇佣。那么你正好雇用一次的概率为 1/n,正好雇用 n 次的概率为 (1/n)^n。这个结果是基于乘法原理得出的,即每个应聘者被雇佣的概率相乘,得到正好雇用 n 次的概率。
需要注意的是,这个计算结果只是一个近似值,因为实际雇用过程中,需要考虑很多复杂的因素,如应聘者的技能和职位的要求是否匹配、你的决策时间和判断力等等。
chatgpt:
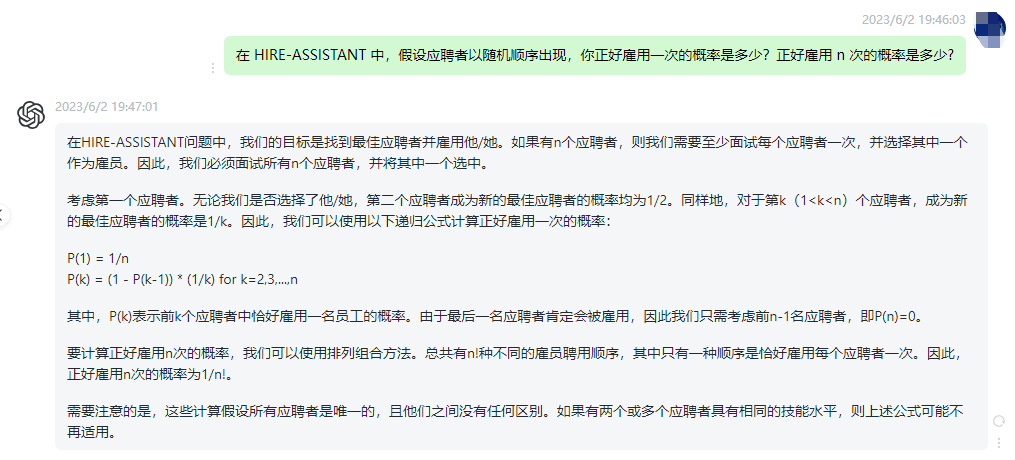
在HIRE-ASSISTANT问题中,我们的目标是找到最佳应聘者并雇用他/她。如果有n个应聘者,则我们需要至少面试每个应聘者一次,并选择其中一个作为雇员。因此,我们必须面试所有n个应聘者,并将其中一个选中。
考虑第一个应聘者。无论我们是否选择了他/她,第二个应聘者成为新的最佳应聘者的概率均为1/2。同样地,对于第k(1<k<n)个应聘者,成为新的最佳应聘者的概率是1/k。因此,我们可以使用以下递归公式计算正好雇用一次的概率:
P(1) = 1/n
P(k) = (1 - P(k-1)) * (1/k) for k=2,3,…,n
其中,P(k)表示前k个应聘者中恰好雇用一名员工的概率。由于最后一名应聘者肯定会被雇用,因此我们只需考虑前n-1名应聘者,即P(n)=0。
要计算正好雇用n次的概率,我们可以使用排列组合方法。总共有n!种不同的雇员聘用顺序,其中只有一种顺序是恰好雇用每个应聘者一次。因此,正好雇用n次的概率为1/n!。
需要注意的是,这些计算假设所有应聘者是唯一的,且他们之间没有任何区别。如果有两个或多个应聘者具有相同的技能水平,则上述公式可能不再适用。