Day50 | 108.冗余连接 109.冗余连接II

108.冗余连接

108. 冗余连接

题目

题目描述

树可以看成是一个图（拥有 n 个节点和 n - 1 条边的连通无环无向图）。

现给定一个拥有 n 个节点（节点标号是从 1 到 n）和 n 条边的连通无向图，请找出一条可以删除的边，删除后图可以变成一棵树。

输入描述

第一行包含一个整数 N，表示图的节点个数和边的个数。

后续 N 行，每行包含两个整数 s 和 t，表示图中 s 和 t 之间有一条边。

输出描述

输出一条可以删除的边。如果有多个答案，请删除标准输入中最后出现的那条边。

思路

定义并查集结构:
- 使用一个数组 father 来表示每个节点的父节点。初始状态下，每个节点都是自己的父节点（即每个节点都代表一个单独的集合）。
初始化并查集 (init 方法):
- 遍历所有节点，将每个节点设置为其自身的父节点。这一步是为了建立每个节点独立的集合。
查找根节点 (find 方法):
- 对于给定的节点 u，如果 u 不是自己的父节点，就递归地查找其父节点的根节点，直到找到根节点为止。在这个过程中，会将路径上的所有节点指向根节点以优化查询效率（路径压缩）。
判断是否在同一集合 (isSame 方法):
- 分别查找两个节点 u 和 v 的根节点，如果它们的根节点相同，则表示这两个节点属于同一个集合。
合并两个集合 (join 方法):
- 查找两个节点 u 和 v 的根节点。如果它们的根节点不同，则将其中一个根节点的父节点设为另一个根节点，从而实现两个集合的合并。
主函数逻辑 (main 方法):
- 从标准输入读取节点数量 n。
- 创建一个 UnionFindExample 实例，并调用 init 方法进行初始化。
- 读取每一对节点 s 和 t，如果它们已经在同一个集合中（通过 isSame 方法判断），则输出这对节点并结束程序；否则，将这对节点所在的集合合并（通过 join 方法）。

代码

import java.util.Scanner;
import java.util.Arrays;public class Main {private int n; // 节点数量private int[] father; // 数组用于存储每个节点的父节点// 构造函数public Main(int n) {this.n = n;this.father = new int[n + 1];Arrays.fill(father, 0);}// 初始化并查集结构public void init() {for (int i = 0; i <= n; ++i) {father[i] = i;}}// 查找给定节点的根节点public int find(int u) {return u == father[u] ? u : (father[u] = find(father[u]));}// 检查两个节点是否属于同一集合public boolean isSame(int u, int v) {u = find(u);v = find(v);return u == v;}// 将两个集合合并，通过链接第二个集合的根节点到第一个集合的根节点public void join(int u, int v) {u = find(u);v = find(v);if (u == v) return;father[v] = u;}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);Main uf = new Main(scanner.nextInt());uf.init();while (scanner.hasNextInt()) {int s = scanner.nextInt();int t = scanner.nextInt();if (uf.isSame(s, t)) {System.out.println(s + " " + t);return;} else {uf.join(s, t);}}}
}

易错点

在 find 方法中，递归地查找根节点的同时，需要更新路径上的每个节点的父节点指向根节点，以减少未来的查找时间

109.冗余连接II

109. 冗余连接II

题目

题目描述

有一种有向树,该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。有向树拥有 n 个节点和 n - 1 条边。如图：

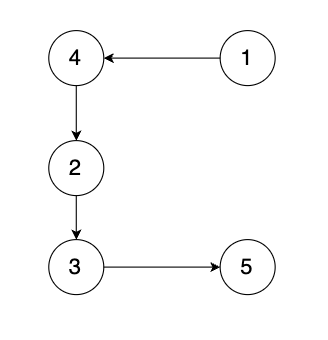
现在有一个有向图，有向图是在有向树中的两个没有直接链接的节点中间添加一条有向边。如图：

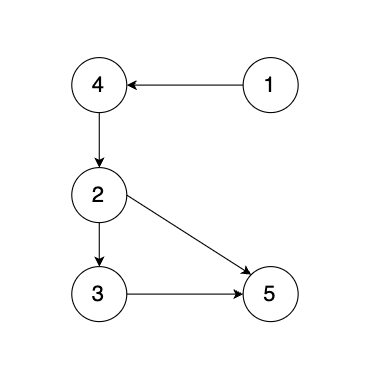
输入一个有向图，该图由一个有着 n 个节点(节点编号从 1 到 n)，n 条边，请返回一条可以删除的边，使得删除该条边之后该有向图可以被当作一颗有向树。

输入描述

第一行输入一个整数 N，表示有向图中节点和边的个数。

后续 N 行，每行输入两个整数 s 和 t，代表这是 s 节点连接并指向 t 节点的单向边

输出描述

输出一条可以删除的边，若有多条边可以删除，请输出标准输入中最后出现的一条边。

思路

初始化并查集: 使用一个数组 father 来表示每个节点的父节点。初始状态下，每个节点都是自己的父节点。
查找根节点 (find 方法): 对于给定的节点 u，如果 u 不是自己的父节点，就递归地查找其父节点的根节点，直到找到根节点为止。在这个过程中，会将路径上的所有节点指向根节点以优化查询效率（路径压缩）。
合并两个集合 (join 方法): 查找两个节点 u 和 v 的根节点。如果它们的根节点不同，则将其中一个根节点的父节点设为另一个根节点，从而实现两个集合的合并。
检测有向环 (getRemoveEdge 方法): 遍历每条边，如果两个端点已经在同一个集合中，则输出这条边并结束程序。
检测删除边后是否为树 (isTreeAfterRemoveEdge 方法): 删除指定的边后，再次遍历所有的边，如果存在环，则返回 false，否则返回 true。
主函数逻辑 (main 方法):
- 从标准输入读取节点数量 n。
- 创建一个 Main 实例，并调用 init 方法进行初始化。
- 读取每对节点 s 和 t，并记录每个节点的入度。
- 根据入度的不同情况选择删除的边。
  - 如果存在入度为2的节点，优先删除最后一条指向该节点的边。
  - 如果不存在入度为2的节点但存在环，删除构成环的任意一条边。

代码

import java.util.Scanner;
import java.util.ArrayList;
import java.util.List;
import java.util.Arrays;public class Main {private int n;private int[] father;public Main(int n) {this.n = n;this.father = new int[n + 1];Arrays.fill(father, 0);}// 初始化并查集public void init() {for (int i = 1; i <= n; ++i) {father[i] = i;}}// 查找给定节点的根节点public int find(int u) {return u == father[u] ? u : (father[u] = find(father[u]));}// 将两个集合合并public void join(int u, int v) {u = find(u);v = find(v);if (u == v) return;father[v] = u;}// 检查两个节点是否属于同一集合public boolean same(int u, int v) {u = find(u);v = find(v);return u == v;}// 在有向图里找到删除的那条边，使其变成树public void getRemoveEdge(List<List<Integer>> edges) {init(); // 初始化并查集for (List<Integer> edge : edges) { // 遍历所有的边if (same(edge.get(0), edge.get(1))) { // 构成有向环了，就是要删除的边System.out.println(edge.get(0) + " " + edge.get(1));return;} else {join(edge.get(0), edge.get(1));}}}// 删一条边之后判断是不是树public boolean isTreeAfterRemoveEdge(List<List<Integer>> edges, int deleteEdge) {init(); // 初始化并查集for (int i = 0; i < edges.size(); i++) {if (i == deleteEdge) continue;List<Integer> edge = edges.get(i);if (same(edge.get(0), edge.get(1))) { // 构成有向环了，一定不是树return false;}join(edge.get(0), edge.get(1));}return true;}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();Main uf = new Main(n);List<List<Integer>> edges = new ArrayList<>();int[] inDegree = new int[n + 1]; // 记录节点入度for (int i = 0; i < n; i++) {int s = scanner.nextInt();int t = scanner.nextInt();inDegree[t]++;edges.add(new ArrayList<>(Arrays.asList(s, t))); // 使用 ArrayList 替代 List.of}List<Integer> vec = new ArrayList<>(); // 记录入度为2的边（如果有的话就两条边）// 找入度为2的节点所对应的边，注意要倒序，因为优先删除最后出现的一条边for (int i = n - 1; i >= 0; i--) {if (inDegree[edges.get(i).get(1)] == 2) {vec.add(i);}}// 情况一、情况二if (!vec.isEmpty()) {// 放在vec里的边已经按照倒叙放的，所以这里就优先删vec.get(0)这条边if (uf.isTreeAfterRemoveEdge(edges, vec.get(0))) {List<Integer> edgeToRemove = edges.get(vec.get(0));System.out.println(edgeToRemove.get(0) + " " + edgeToRemove.get(1));} else {List<Integer> edgeToRemove = edges.get(vec.get(1));System.out.println(edgeToRemove.get(0) + " " + edgeToRemove.get(1));}return;}// 处理情况三// 明确没有入度为2的情况，那么一定有有向环，找到构成环的边返回就可以了uf.getRemoveEdge(edges);}
}