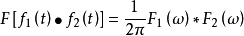---

什么是 Shaarli ？

Shaarli 是一个使用 PHP 编写的针对个人、极简、超快速、无数据库的书签服务。

安装

在群晖上以 Docker 方式安装。

在注册表中搜索 shaarli ，选择第一个 shaarli/shaarli，版本选择 latest。

卷

在 docker 文件夹中，创建一个新文件夹 shaarli，并在其中建四个子文件夹，分别是 cache 、 data、plugins、tpl

文件夹	装载路径	说明
docker/shaarli/cache	/var/www/shaarli/cache	缓存
docker/shaarli/data	/var/www/shaarli/data	存放数据、设置等
docker/shaarli/plugins	/var/www/shaarli/plugins	存放插件，为可选
docker/shaarli/tpl	/var/www/shaarli/tpl	存放主题，为可选

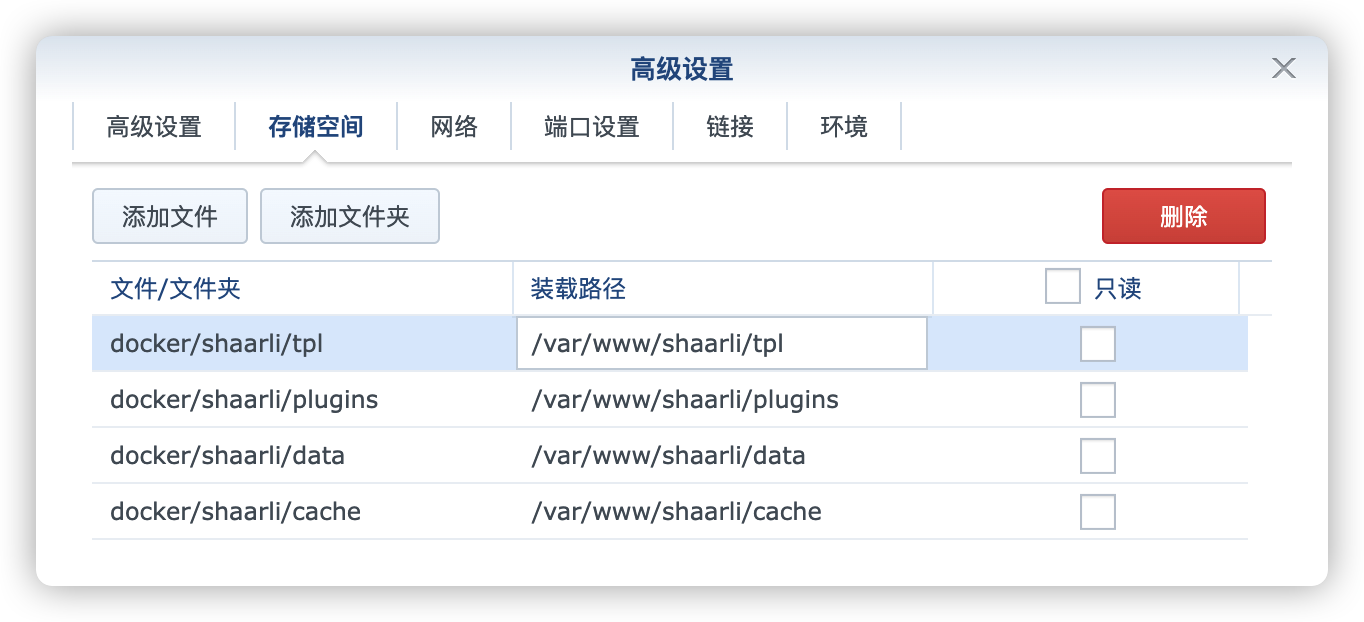
如果不用插件和主题，只挂载两个目录也是可以运行的

端口

本地端口不冲突就行，不确定的话可以用命令查一下

# 查看端口占用
netstat -tunlp | grep 端口号

本地端口	容器端口
9380	80

命令行安装

如果你熟悉命令行，可能用 docker cli 更快捷

# 新建文件夹 shaarli 和 子目录
mkdir -p /volume2/docker/shaarli/{cache,data,plugins,tpl}# 进入 shaarli 目录
cd /volume2/docker/shaarli# 运行容器
docker run -d \--restart unless-stopped \--name shaarli \-p 9380:80 \-v $(pwd)/cache:/var/www/shaarli/cache \-v $(pwd)/data:/var/www/shaarli/data \-v $(pwd)/plugins:/var/www/shaarli/plugins \-v $(pwd)/tpl:/var/www/shaarli/tpl \shaarli/shaarli:latest

也可以用 docker-compose 安装，将下面的内容保存为 docker-compose.yml 文件

version: '3'services:shaarli:image: shaarli/shaarli:latestcontainer_name: shaarlirestart: unless-stopped   ports:- 9380:80volumes:- ./cache:/var/www/shaarli/cache- ./data:/var/www/shaarli/data- ./plugins:/var/www/shaarli/plugins- ./tpl:/var/www/shaarli/tpl

然后执行下面的命令

# 新建文件夹 shaarli 和 子目录
mkdir -p /volume2/docker/shaarli/{cache,data,plugins,tpl}# 进入 shaarli 目录
cd /volume2/docker/shaarli# 将 docker-compose.yml 放入当前目录# 一键启动
docker-compose up -d

运行

在浏览器中输入 http://群晖IP:9380 就能看到安装界面

设置好账号、密码，时区选择 Asia/Shanghai，完成后点 install

设置完成就可以登录了

登录成功后的主界面

插件

代码主页：https://github.com/shaarli/Shaarli

下载代码

本地解压之后，将这两个目录上传到 docker/shaarli 目录，覆盖上传

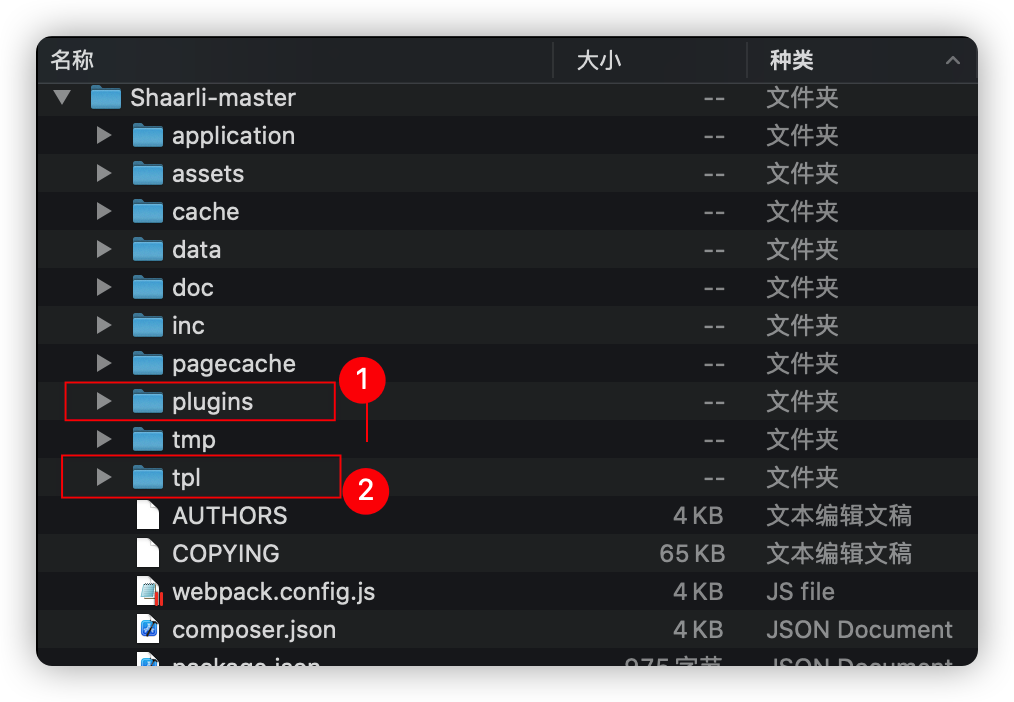
上传完成后

进入 工具 --> 插件管理

主题

进入 工具 --> 配置 Shaarli

似乎还没有 default 的好看，而且也没有汉化

chrome 插件

在 Chrome 商店中搜索 shaarli

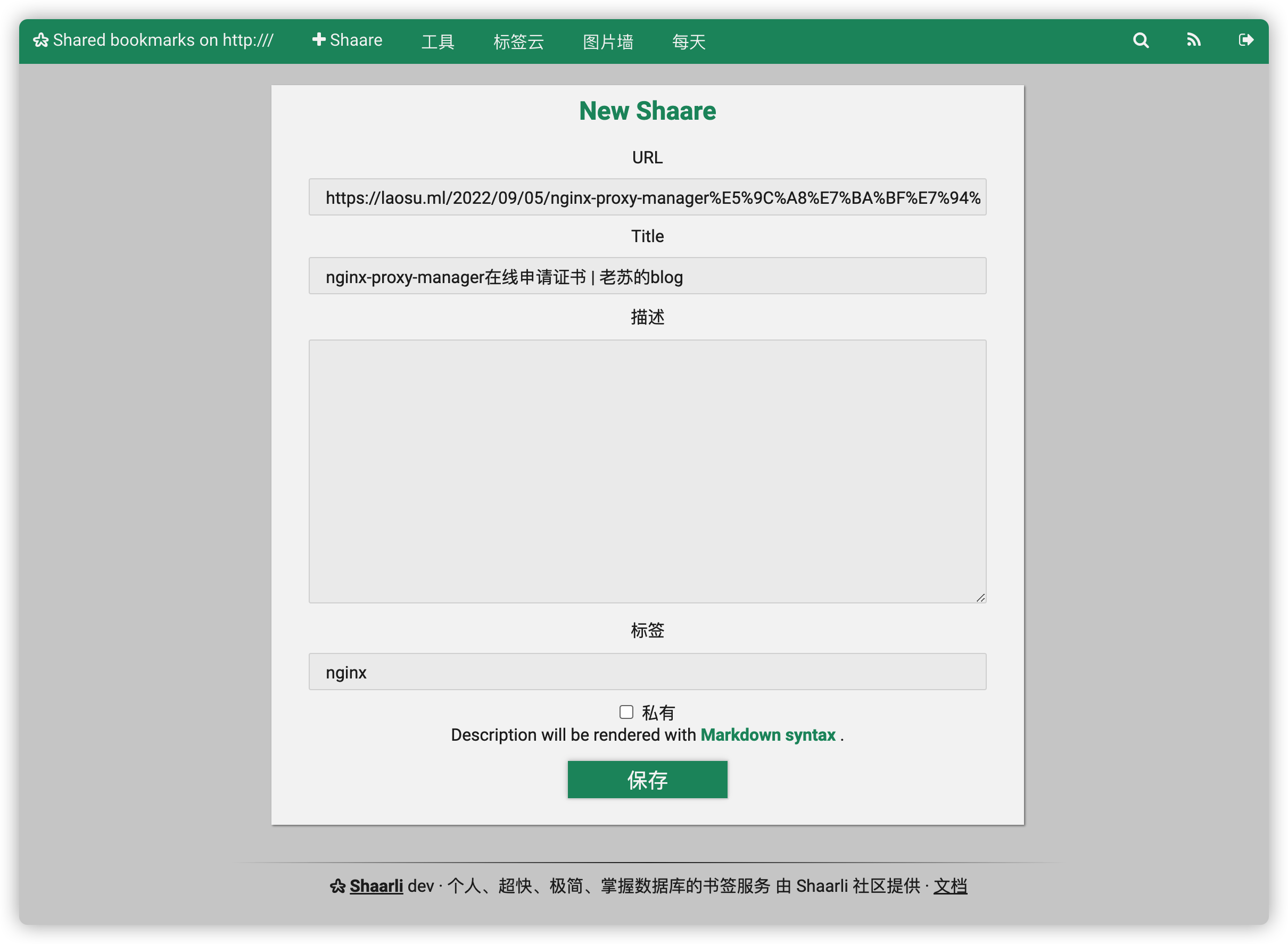
老苏装了第一个 Add to Shaarli，只要设定服务器地址就可以了

公网使用要先做反代，填入相应的域名；

在想收藏的页面点插件按钮

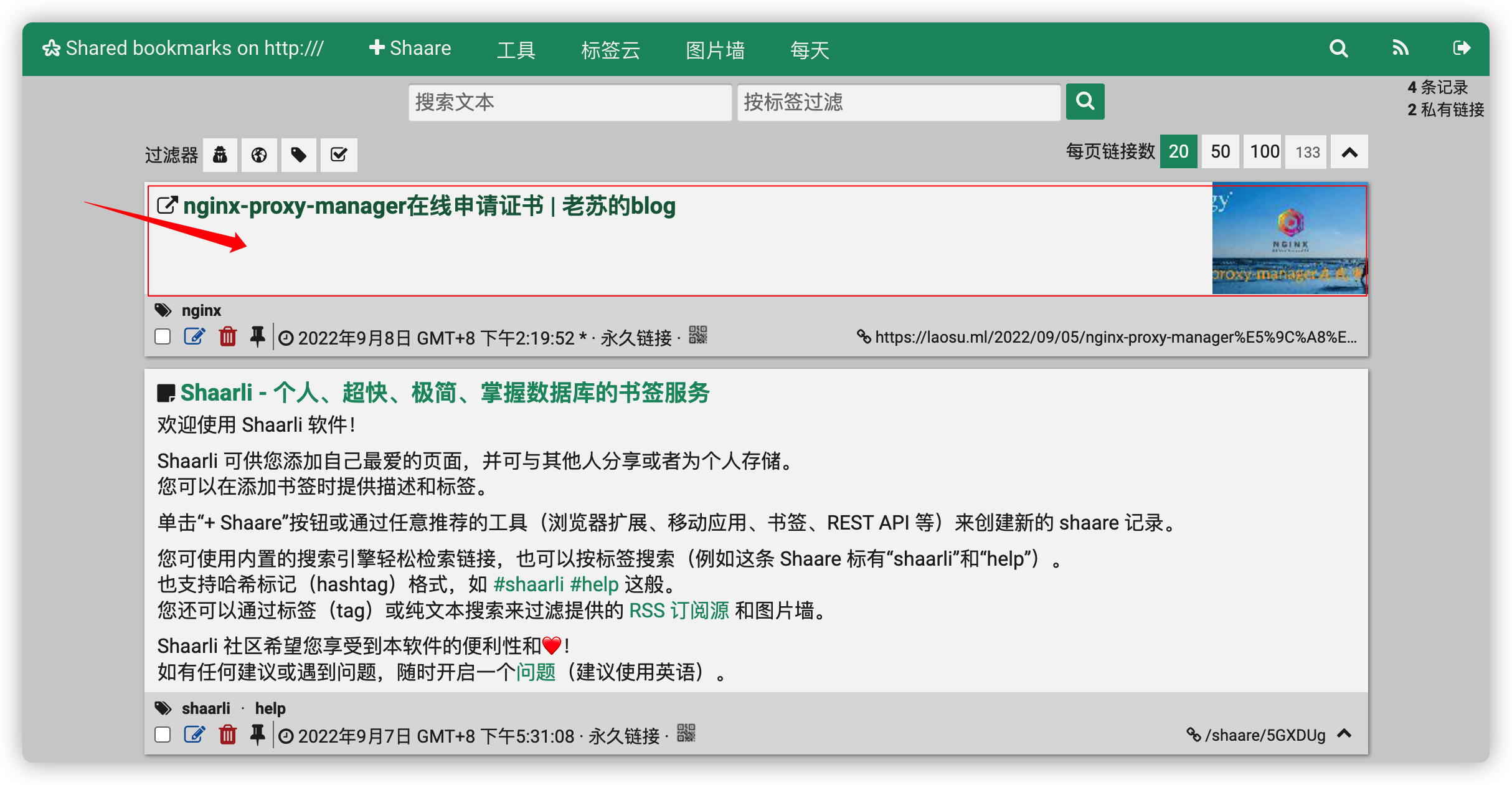
保存之后，可以在 Shaarli 主界面看到

移动端就留给大家自己去研究了

参考文档

shaarli/Shaarli: The personal, minimalist, super-fast, database free, bookmarking service - community repo
地址：https://github.com/shaarli/Shaarli/

Docker - Shaarli Documentation
地址：https://shaarli.readthedocs.io/en/master/Docker/