引言

在自然科学的许多领域特别是科学与工程计算中，经常会遇到常微分方程的求解问题。然而只有非常少数且十分简单的微分方程可以用初值等方法求得它们的解，多数只能近似方法求解。

一、预备知识 （差商的推导）

 二、 一阶常微分方程数值解

 （1）初值问题

（2）欧拉公式推导

注意： 并不是说相等，只是近似解。

（3）例题代码实现

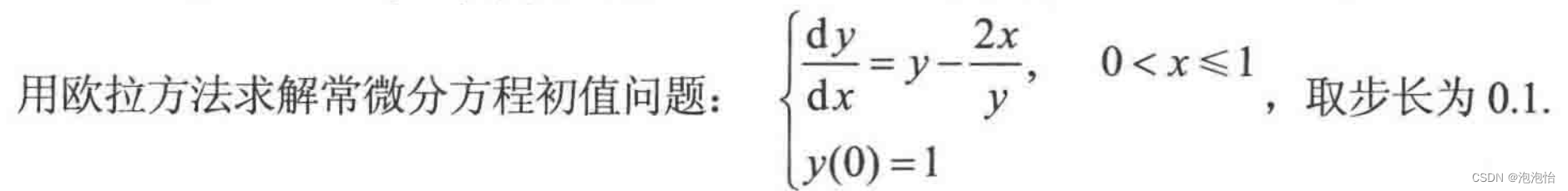
准确解： 

import numpy as npdef f(x,y):return y-2*x/ydef exact_f(x):return np.sqrt(1+2*x)
x0=0
y0=1
h=0.1
n=10
x=np.zeros((n+1))
y=np.zeros((n+1))
exact_y=np.zeros((n+1)) #精确解
r=np.zeros((n+1))       #误差
x[0]=x0
y[0]=y0
exact_y[0]=exact_f(x[0])for i in range(n):x[i]=x[0]+i*hx[i+1]=x[0]+(i+1)*hy[i+1]=y[i]+h*f(x[i],y[i])exact_y[i+1]=exact_f(x[i+1])r=np.abs(y-exact_y)
import pandas as pddata=np.vstack((x,y,exact_y,r))
data=data.T
df=pd.DataFrame(data,columns=['xi','欧拉方法yi','精确解y(xi)','误差|yi-y(xi)|'])
df=df.drop([0])
df

 结果如图：

 发现光，追随光，成为光，散发光。