序言
最近迷上了原神这款游戏,趁着保研完,肝了两个星期,也氪了一些金。先不谈这款游戏可玩性有多高,但论氪金强度算是我从小到大玩的游戏中,能排得上第一的了。
对于这种寸卡寸金的游戏,如何在无穷无尽的抽卡活动中,做到理性抽卡,无疑需要严谨的数学分析,才能了解大概氪多少金才能满足自己的预期。本文将对此做出一定的解答。
同时,本文对于网上一直所传的氪不改命,玄不救非之说,也将进行一定的抨击。
假设陈述
- 原神抽奖卡池,在非保底的情况下,抽到五星的概率为基础概率,即0.6%
符号说明
| 符号 | 含义 |
|---|---|
| X X X | 表示在平均概率下进行 独立重复试验中第一次 抽到五星的次数的随机变量 |
| P ( s u c c e s s ) P(success) P(success) | 表示抽到五星的平均概率 |
| P ( b o t t o m ) P(bottom) P(bottom) | 表示保底情况出现的概率 |
| P ( b a s e ) P(base) P(base) | 表示抽到五星的基础概率 已知:0.6% |
| n n n | 表示保底在第几次未抽中时出现 已知:90 |
| P ( s u c c e s s ∥ b o t t o m ) P(success\|bottom) P(success∥bottom) | 表示在保底情况下抽中五星的概率 已知:1 |
| P ( s u c c e s s ∥ b o t t o m ‾ ) P(success\|\overline{bottom}) P(success∥bottom) | 表示在非保底情况下抽中五星的概率 已知: P ( b a s e ) P(base) P(base) |
目标变量
P ( s u c c e s s ) P(success) P(success)
求解方法
-
法一:
运用全概率公式,写出方程组,直接进行求解。
{ P ( b o t t o m ) P ( s u c c e s s ∥ b o t t o m ) + P ( b o t t o m ‾ ) P ( s u c c e s s ∥ b o t t o m ‾ ) = P ( s u c c e s s ) P ( s u c c e s s ) ( 1 − P ( b a s e ) ) n − 1 = P ( b o t t o m ) \left\{\begin{matrix} P(bottom)P(success\|bottom)+P(\overline{bottom})P(success\|\overline{bottom})=P(success) \\ P(success)(1-P(base))^{n-1}=P(bottom) \end{matrix}\right. {P(bottom)P(success∥bottom)+P(bottom)P(success∥bottom)=P(success)P(success)(1−P(base))n−1=P(bottom)
代入,得:
{ P ( b o t t o m ) + 0.006 ( 1 − P ( b o t t o m ) ) = P ( s u c c e s s ) P ( s u c c e s s ) ( 1 − 0.006 ) 89 = P ( b o t t o m ) \left\{\begin{matrix} P(bottom)+0.006(1-P(bottom))=P(success) \\ P(success)(1-0.006)^{89}=P(bottom) \end{matrix}\right. {P(bottom)+0.006(1−P(bottom))=P(success)P(success)(1−0.006)89=P(bottom)
求解,得:
P ( s u c c e s s ) = 0.01435 ± 0.000005 P(success)=0.01435\pm0.000005 P(success)=0.01435±0.000005 -
法二:
通过间接求解,在平均概率下进行独立重复试验中第一次抽到五星的次数的期望,进行求解。
E [ X ] = ∑ i = 1 n − 1 i ∗ P ( b a s e ) ( 1 − P ( b a s e ) ) i − 1 + n ∗ ( 1 − ∑ i = 1 n − 1 P ( b a s e ) ( 1 − P ( b a s e ) ) i − 1 ) = ∑ i = 1 89 i ∗ 0.006 ( 1 − 0.006 ) 89 + 90 ∗ ( 1 − ∑ i = 1 89 0.006 ( 1 − 0.006 ) 89 ) ≈ 69.6998 E[X]=\sum_{i=1}^{n-1}i*P(base)(1-P(base))^{i-1}+n*(1-\sum_{i=1}^{n-1}P(base)(1-P(base))^{i-1}) \\ \quad \\ =\sum_{i=1}^{89}i*0.006(1-0.006)^{89}+90*(1-\sum_{i=1}^{89}0.006(1-0.006)^{89}) \\ \quad \\ \approx69.6998 E[X]=∑i=1n−1i∗P(base)(1−P(base))i−1+n∗(1−∑i=1n−1P(base)(1−P(base))i−1)=∑i=189i∗0.006(1−0.006)89+90∗(1−∑i=1890.006(1−0.006)89)≈69.6998
P ( s u c c e s s ) = 1 E [ X ] P(success)=\frac{1}{E[X]} P(success)=E[X]1(这个等式,概率论那本书上好像没有,不过我自己私下里证明过了,感兴趣的同学可以自行证明)
那么,可以得到与法一相同的结果,证明了结果的正确性。
结论
可以看到的是我们得出的平均概率1.435%是略小于官方给出的平均概率1.6%的。
很显然,这说明,即使在未保底的情况下,我们抽中五星的概率可能并非是基础概率0.6%。
结合这几天,我看的PDD抽奖的视频,我发现确实在一些之前很非的情况下,后面抽到五星的频率显著变高。
当然,我并不清楚原神抽奖内部究竟是怎样的机制,不过或许可以借助这一点,再结合一些大佬的分析,在五十抽向后的概率或许确实有一定的提升。所以大家注意好这点,抽双黄吧!
当然,这也仅仅是概率的提高,可能样本量少一点的话,在实际抽奖中,根本感觉不到那种概率的提升。所以,也仅供大家参考。同时,大家也要考虑一下自己的经济水平究竟如何,有多大经济水平,有多大期望。
这里我用python做了一个小实验,用直方图展示10000个玩家,在我上述假设的那种情况下抽奖2000次,抽到五星的次数,并与无保底的转换平均概率(0.01435)进行了比较。
# -*- coding: utf-8 -*-import matplotlib.pyplot as plt
import random
import numpy as np
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']random.seed(0)
data1=[]
data2=[]
n=10000
epoches=2000
prob=0.006
prob_trans=0.01435for i in range(n):curcnt=0counter=0for epoch in range(epoches):rand=random.random()counter+=1if rand<prob:curcnt+=1counter=0if counter==90:curcnt+=1counter=0data1.append(curcnt)plt.subplot(121)
plt.hist(data1,bins=np.linspace(10,50,20),density=False)
plt.xlim(10,50)
plt.ylim(0,4000)
plt.title('90次保底情况')for i in range(n):curcnt=0for epoch in range(epoches):rand=random.random()if rand<prob_trans:curcnt+=1data2.append(curcnt)plt.subplot(122)
plt.hist(data2,bins=np.linspace(10,50,20),density=False)
plt.xlim(10,50)
plt.ylim(0,4000)
plt.title('无90次保底情况(基础概率已经过转换)')
plt.show()
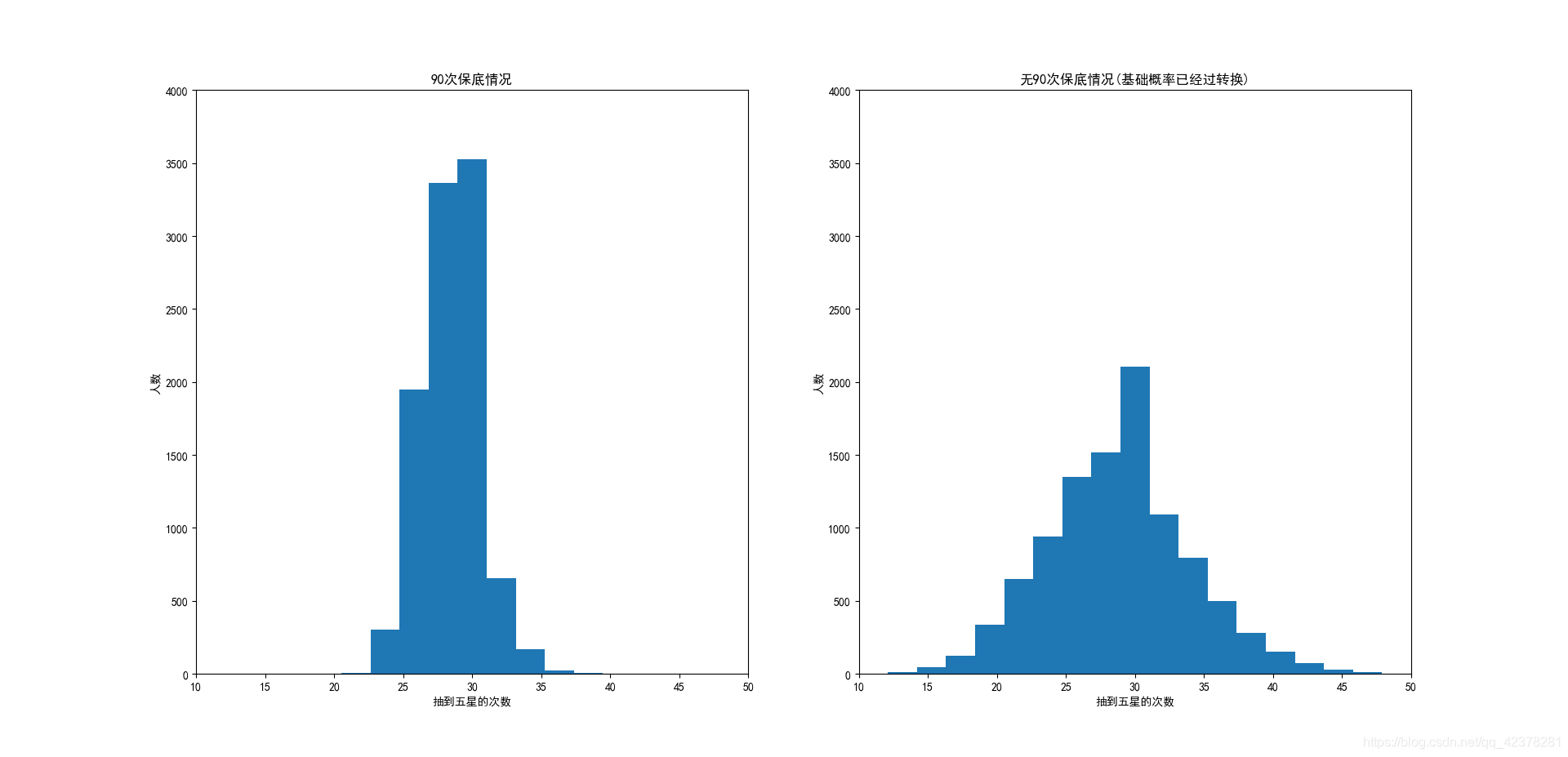
从左图中,大家可以估计一下,自己抽多少次,能拿到多少五星。
同时,通过上图的对比,可以看出,在原神抽奖的机制下,并不会出现,特别非酋,或者特别欧皇的情况。最非酋和最欧皇的,也就是一倍之差。所以,大家也不要相信网上那些一个十抽多少黄的视频了,肯定是P的。
即使出了双黄的兄弟,之前也是大概率流下过非酋的眼泪。
所以,这个游戏,没有绝对的非酋,也没有绝对的欧皇,合理估计自己能拿到的五星,不要有非分之想,方为正途!