项目场景:
由于最近在做一个项目的cola代码改造,所以由于cola需要在 service 和 dao层中间加一层>>> gateway,和springcloud中的gateway不一样,这个仅仅是抽象了一层;
思考: 现在我的事务 依然在service中开启,那么我的事务经过了一个gateway后,再次调用dao层,事务是否会生效?
1 生效, 如果这样,那么事务加载控制器应该也是生效的吧?
2 不生效, 那么难道一个springboot项目要采用 seta 分布式事务处理?
问题描述
开始百度~~~~~

意思是spingboot 中在控制器添加了事务,会不生效
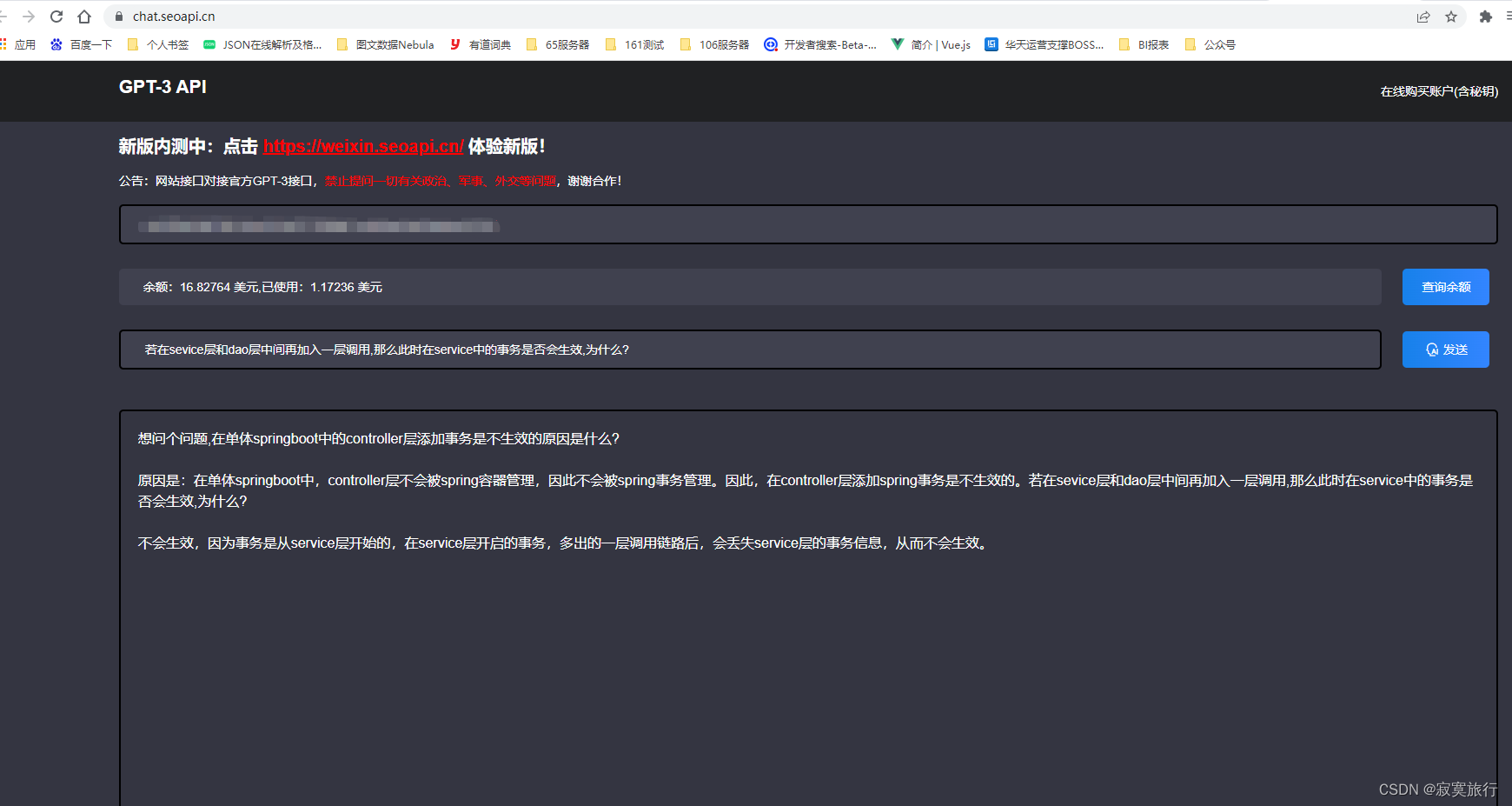
问了下 chatgpt 回答是:
1 控制器添加事务会失效,因为controller 会被纳入springmvc容器,serivce 和 dao等会被纳入到spring容器;
2 在service 和 dao层中间加了一层,会导致失去事务信息,从而导致事务失败!!!

原因分析:
我真的是被各种回答搞的不知所措,无论哪个答案,两个之前都是互相说不通,我决定自行验证
自己验证的一个视频
最终的结论是:
● 在controller中开启事务,也是生效的: 因为事务加在了数据源上
● 若在sevice层和dao层中间再加入一层调用,那么此时在service中的事务 事务依然生效: 因为相当于无论代理了多少层,最终事务还是加在了数据源上;
但是具体原因 不得而知,我仅仅是猜测,只要是事务直接加在了或者间接加在了支持事务的数据源(例如mysql 的innodb)上,那么事务就会生效;
那么ChatGTP的回答,在我这里是错误的,不知道是不是我自己的问题;还是它错了,实践出真知,我觉得它错了,后面的一个博主的回答,也从侧面证明了它的错误;
解决方案:
一位博主的回答:
在Spring Boot中添加事务,需要满足以下条件:
确保应用程序已经正确配置了数据源和事务管理器。
事务必须被@Transactional注解标注。
在需要应用事务的方法中调用了其他的标记了@Transactional注解的方法,即使用到了AOP代理。
如果以上三个条件都满足,那么在Controller层添加事务应该是有效的。如果不生效,可以考虑检查是否满足以上三个条件。
如果在Service层和DAO层之间添加了一层调用,那么在Service中的事务仍然会生效,因为Spring使用的是基于代理的事务管理。代理类会包装调用目标方法的对象,以便在方法执行时启用事务管理。只要@Service注解添加到该类中,并且在调用方法上使用了@Transactional注解,代理类将为目标方法添加事务。因此,在Service层和DAO层之间添加另一层调用不会影响事务管理的工作原理。
请大神留言给予更好的答案和解释~~