以往leader-aware算法

核心思想： 随机选择网络中的leader节点，然后分配剩余节点。

如何随机选择：

1. LICOD - “中心性指标”（节点的重要性）确定领导者，根据度将剩余节点分配到不同社团

2. HDA - 找“领导对”，基于领导构建依赖树

   缺点： 社区检测仅基于网络的拓扑信息

3. aLBDC - 拓扑信息缺失时，使用属性信息分配领导者

   缺点： 属性信息仅作为拓扑信息的补充，在算法开始时并没有将两者完全结合

创新点

1. TALB是第一个在数据预处理阶段结合网络拓扑信息和属性信息进行社区检测的基于领导的算法
2. 提出了一种新的节点关系矩阵C，该矩阵依据矩阵元素正负寻找节点

问题定义

定义基础概念

1. 邻接矩阵A∈R n×n来表示网络的拓扑信息 当且仅当节点i和j之间存在边时，Aij = 1，否则Aij = 0

2. 属性信息矩阵W∈R n×m，其中n为节点个数，m为特征个数 在这个矩阵中，Wij是节点i的第j个特征 如果节点i具有属性j，则Wij =
   1，否则Wij = 0

3. 无向无权图中，定义节点u的拓扑邻居
   

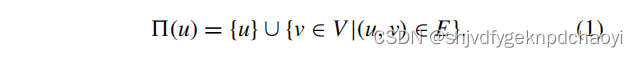
4. 用拓扑邻居定义Jaccard相似系数J(i, J)（Jaccard相似系数的值越高，节点之间的相似度越高）
   

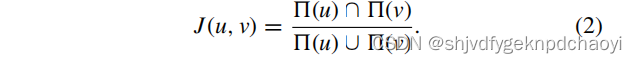
5. 由网络的邻接矩阵A得到节点关系矩阵R∈R n×n，其中Rij取J(i, J)的值

6. 根据节点属性，获得Pearson相关系数（Pearson相关系数的绝对值越大，节点之间的相关性越强）
   

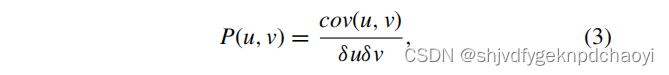
7. 由节点间的Pearson相关系数，得到节点间的属性关系矩阵S∈R n×n，其中Sij取P(i, j)的值

总结：获得了 节点关系矩阵R & 属性关系矩阵S，两个矩阵以不同的方式表达了网络中节点之间的关系，这种关系也可以看作是节点之间的边权。

定义创新概念

1. 信息矩阵I，它是两个矩阵的组合。
   
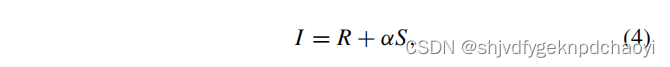
   （α是控制属性信息权重的参数）

2. 每个节点V∈V的领导权等于该节点与其所有相邻节点的相关度总和
   

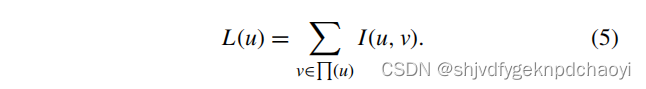
模型构造

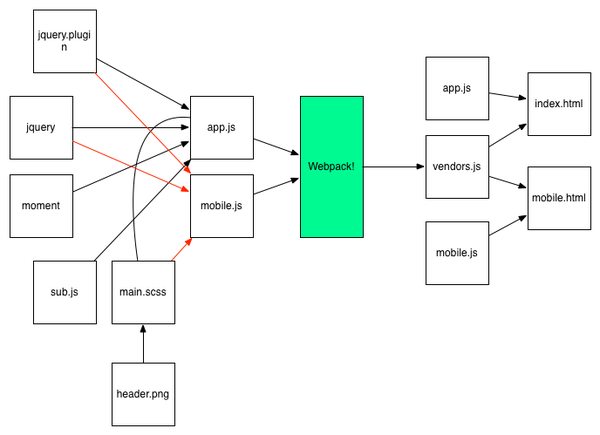
• TALB算法的流程图。
  算法主要包括两个步骤:

1. 寻找leader形成本地社区(绿框中，每个节点寻找自己的本地leader(节点1和节点2));
2. 合并分支，得到最终的聚类结果(橙色框中处理孤立点，形成最终的群落结构)。

第一步：确定每个节点的leader

1. 遍历网络中的每个节点，计算每个节点的领导能力L(u)，并与L(v)进行比较，其中v是u的拓扑邻居（定义3.）。本文认为所有满足条件L(v) > L(u)的节点都是节点u的候选领导集合

2. 对于一个节点u，可能有多个相邻节点同时具有领导L(·)> L(u)
   为了从leader候选集合中选择合适的leader，根据两个节点是否属于同一个社区，作为判别的附加条件。
   如果是一个社区，则可以互为leader
   考虑到当两个变量之间的关系为负时，皮尔逊相关系数为负，本文利用信息矩阵I（信息矩阵，创新定义1.）进一步细化领导者候选人集
   如果Iij < 0，则认为两个节点不属于同一个社区，这就主动说明了节点i、j不能互为leader

3. 除此之外，我们还应用了Attractive force来进一步优化leader
   若v是u的拓扑邻居（定义3.），V对节点u的引力公式为：
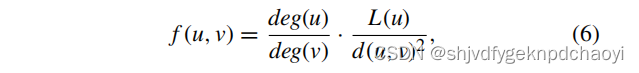   （deg(u)为节点u的度数，d(u, v) = 1 / I (u, v) ）
   （ I (u, v)：信息矩阵，创新定义1.）

4. 给定无向无权图G = (V, E)，节点V∈V的局部前导为：
   

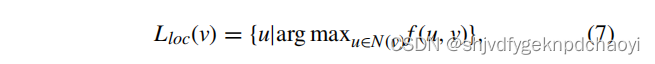
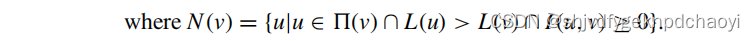
注意，在执行上述计算之后，局部前导Lloc(v) 可能是一个空集。
出现这种情况的具体原因是，导联L(u) 是一个局部极值。

6. 经过上述条件的计算，我们可以确定每个节点的唯一本地leader

在以上计算结束时，我们可以得到一个初始的本地leader集合，我们不需要提前知道网络的真实社区数量。

第二步：合并小分支以得到最终结果

1. 完成上述步骤后，我们得到了由每个节点的局部信息形成的初步聚类结果。
   然而，由于我们只使用了当地的信息，可能会有一些细微的分支由于原始数据的模糊性而分类错误，例如孤立的点。
   因此，为了得到更准确的结果，我们必须合并最初围绕当地领导人形成的小社区(因为在合并过程中我们只考虑每个领导人之间的关系)。

2. 首先，如果存在一个离群值，我们将其视为邻近节点中领导能力最强的节点的追随者。
   如果有多个邻居的领导能力最强，则选择程度最高的邻居作为其当地领导人。

3. 然后利用信息矩阵I（包含属性和拓扑信息）中的元素判断两个前导是否需要合并，本文设置I(u, v) > 1为合并(阈值视实际情况而定)。

实验

数据集

人工合成网络

1. 标准Lancichinetti-Fortunato-Radicchi (LFR)基准网络模型通常用于评估社区检测算法，因为它提供了对真实网络的良好近似。
   我们用来生成网络的参数如表(1)所示。
   网络结构的复杂性随着混合参数µ的增大而增大。

   每个节点构造了m维0-1属性信息向量，其中m为属性个数
   在本文中，我们将为每个社区提供50个相应的属性。
   显然，属于同一个通信社区的节点应该具有高概率的相同属性。
   进一步，假设网络中有h个社区，那么每个节点对应的属性就有50 × h个。

   更详细地说，我们使用概率ρin的二项分布来生成属于团体的节点的0-1属性，使用概率ρout的二项分布来生成剩余的属性。
   在随后的实验中，我们分别为ρin和ρout选择了三个不同的值，其中ρin ={0.8, 0.7, 0.6}和ρout ={0.2, 0.3, 0.4}。
   显然，更大的ρin (ρout)使网络结构更清晰(更模糊)。

现实世界的网络

1. Zachary空手道网： 理念上的分歧导致了俱乐部主任和空手道教练之间的争执，成员们围绕他们支持的领导人组建了两个新的内部组织。
   我们会看到网络中的节点代表每个成员，当两个成员成为朋友(例如，一起看电影，去参加聚会)，我们可以在相应的节点之间建立链接。

2. 橄榄球网： 橄榄球网是根据2000年NCAA的美国大学橄榄球联盟建立的网络。
   联盟将115支参加比赛的球队分成12个区(12个社区)进行比赛。
   网络中的节点代表橄榄球队(共115个节点)，我们在任何两支球队之间构建一个链接(即一条边)，只要他们进行了一场比赛。
   网络中有616个边，这意味着整个联赛总共进行了616场比赛。

3. 海豚网络： 一个社交网络，由62个节点代表62只宽鼻子海豚。
   作为除人类之外拥有复杂社会网络的物种之一，栖息在新西兰海湾的海豚网络的复杂性不亚于人类的网状工作。
   海豚由两位领队带领，分为两个科(群落数量为2个)。
   当两只海豚中的一只互相交流，超过了定义的亲密值，我们就在相应的节点之间建立联系

4. Polbooks网络： 这个网络的节点是由亚马逊美国网站上所有与政治相关的书籍组成的，根据页面底部的“买了这本书的人也买了…”
   V. Krebs根据在亚马逊上的分类将这些书分为三类(“自由主义”、“保守主义”和“中间派”)。

5. WebKB network： 数据集是四所大学(康奈尔大学、德克萨斯大学、华盛顿大学和威斯康辛大学)的信息网络的集合。
   每所大学的网络工作分为五个类，包括课程类、学生类、教员类、项目类和教员类。
   每个出版物都有1703个属性，这些属性由二进制向量表示，表示单词的存在或不存在。

基线方法和评估指标

对比算法

Topleaders，HDA 和 autoLeader

评价指标

1. 归一化互信息(NMI）：
   

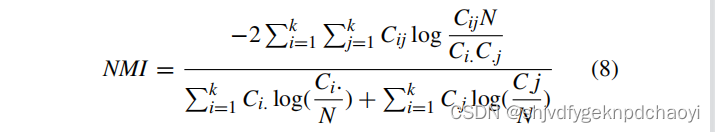
（其中N为节点数，k为社区数，Cij为社区i中分配给社区j和Ci的节点数。Ci.为矩阵C的第i行之和，log为自然对数。）
（NMI的值在[0,1]之间。）

2. Kappa：Kappa考虑了随机效应的影响，其计算公式如下:
   
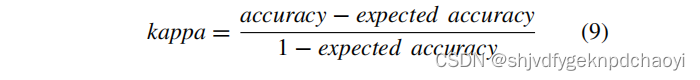
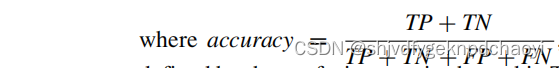
3. Purity：正确分配的节点数除以v中节点总数。纯度范围从0(完全不一致)到1(完全一致)。
   
   （M和Q是相同数据的两个不同分区，V是所有节点的集合。）

实验结果

人工合成网络

这些网络由不同的混合参数µ来研究不同的参数α（信息矩阵，顶概念定义1.）对TALB结果的影响。可以观察到:

1. 随着网络变得越来越复杂(即ρin减小，ρout增大)，群落检测变得越来越困难，从而降低了TALB的准确性。
2. 即使在高噪声网络(ρin = 0.6， ρout = 0.4)中，本文提出的TALB共同体检测结果也是可以接受的。
   当网络的属性信息(ρin = 0.8， ρout = 0.2)明确时，算法的准确率可达0.95。
3. 实验结果表明，参数α的不同值对不同数据集的结果影响不大，这意味着在未来的实际计算中不需要对α进行特殊的手动调整，可以设置为1。

接下来，我们进行实验，将TALB模型与目前使用较为广泛的其他基于领导的模型进行准确性比较，如表(4)所示。注意表中的TALB82、73、64表示所使用的不同属性信息。
例如，TALB82表示为每个节点生成一个属性向量，参数ρin = 0.8，ρout = 0.2。

1. 从表中可以看出，当属性信息清晰时，提出的TALB算法的性能几乎是最佳的，当属性信息模糊时，结果仍然比不结合属性信息进行团体检测的Top leaders更准确。
2. TALB的稳定性和普适性也很明显，这也说明仅使用网络的拓扑信息进行社区检测是不够的。

真实网络

我们首先实验了不同参数α值对TALB结果的影响，如图(3)所示。
从图中可以看出:

1. 每个数据对于自己取的最大值对应一个特定的α值，但α的值对整个算法的结果没有显著的影响。
   因此，在实际计算中，当不存在其他特殊情况时，我们设α = 1。
2. 属性信息更加清晰，增强了社群检测结果，验证了关键作用
3. 当属性信息异常嘈杂时，属性信息中包含的团体结构模糊，但TALB的精度在0.4以上，说明TALB能够很好地结合网络拓扑信息和节点属性信息。

然后，将TALB与几种不同的算法在真实网络中进行比较，具体结果如表(5)和表(6)所示。结果显示:

1. 当属性信息为表(5)和表(6)时，算法TALB具有较高的团体检测结果，这表明该信息不仅是对网络拓扑信息的补充，而且在正交上为检测提供了有用的信息。
2. 我们提出的TALB方法在极其模糊的属性信息中也表现良好，从侧面反映了TALB方法的鲁棒性，即我们的算法的功能并不完全依赖于节点属性中明确而清晰的信息。
3. TALB的准确率随着属性信息的模糊而降低，进一步说明高质量的节点属性信息在社区检测中起着至关重要的作用。
   此外，我们还比较了几种算法的计算时间。
   由图(4)可以看出，虽然Top leader的计算时间最短，但该算法的计算精度并不高。
   本文提出的TALB算法在保证精度的前提下，具有较短的计算时间。