作者：北京大学苟向阳

 

编者按：

现代社交网络极大地促进了信息的生成和传播，也加剧了不同信息对用户注意力的竞争。

对于一条信息的传播范围进行预测，能够帮助运营者和用户提前发现潜在的热点，从而为其决策提供指导。

本文将介绍两种基于深度学习的信息传播预测算法。

 

问题定义

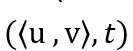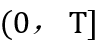信息传播预测，即为基于一条信息当前的传播路径，预测信息未来的传播范围。具体来说。一条信息在社交网络上的传播可以被抽象为一个传播图 (cascade graph)， 如下图所示。传播图上的每一个点代表社交网络上的一个用户，而边则表示该信息被用户 v 转发自用户 u 。t 指从该信息第一次被发布（下图中的）到该次转发之间经过的时间。给定一个观察窗口, 我们已知此时间窗口内的所有转发，即 T 时刻为止的传播图。我们需要以此为根据，预测该信息未来还会被转发多少次。

 

 

背景工作介绍

早期的信息传播预测主要有两类方式。一类是基于特征的方法：这类方法靠使用者手工提取特征，如信息的内容特征，当前传播的时序特征，结构特征，传播路径上的用户特征等。基于这些特征，使用回归 (regression) 算法来预测信息转发次数。这一类方法的效果非常依赖于特征的提取，对于不同的问题，需要使用者根据自己经验来提取合适的特征。第二类是生成式算法，这类算法设计模型来模拟信息传播机制，力图将信息传播的主要特点保留在模型中，然后运用该模型来计算每一条信息在未来的传播范围。这类算法的主要问题在于预测能力有限，因为其使用的模型一般来自于一些泛用数学模型，如强化泊松过程，而不能准确模拟信息传播。本文介绍的两种方法为生成类算法与深度学习算法的结合。它们将生成类方法中利用的信息传播特点，如自我激励（self-exciting），衰减机制（time decay effect）等，与深度学习相结合，从而在保持可解释性的同时获得更强的预测能力。

DeepHawkes

DeepHawkes 算法来自于2017年CIKM论文《DeepHawkes:  Bridging the Gap between Prediction and Understanding of Information Cascades》[1]。该算法将Hawkes 过程与深度学习方法结合。它利用了Hawkes过程中的3个主要机制：1. 用户影响力，不同的用户具有不同的影响力，高影响力用户对于信息传播具有更大贡献。2. 自我激励机制：历史上的每一次转发都使得该信息在未来被转发的可能性提升。3.时间衰减机制：历史转发的影响力会随着时间衰减。

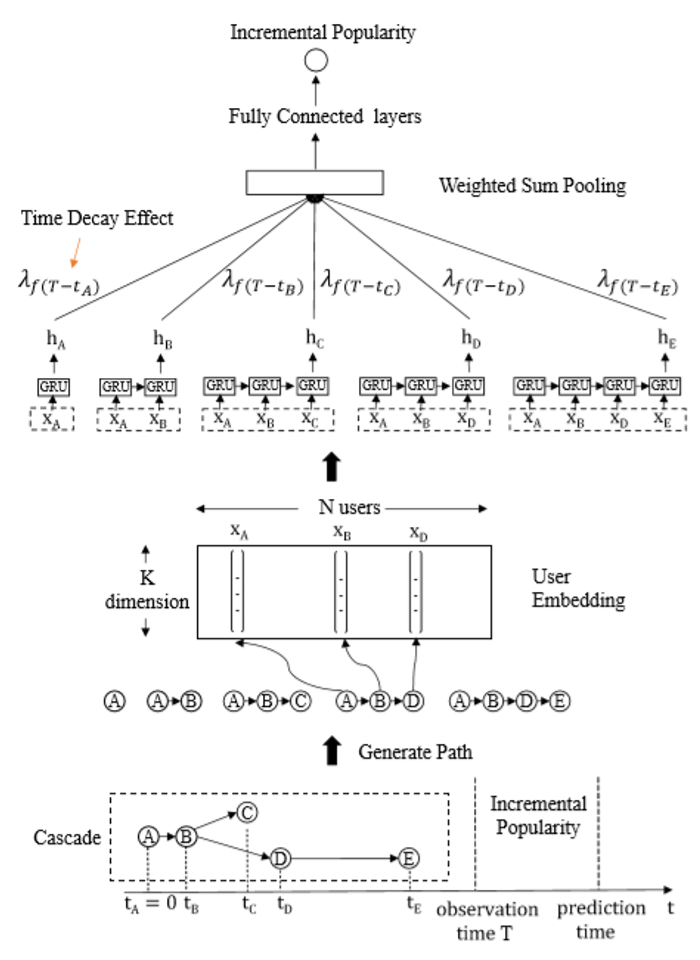
DeepHawkes结构如下图。它将传播图表示为一系列的传播路径，每一条传播路径代表信息从起始点到达某一个用户的过程。DeepHawkes 由 3个部分组成，第一部分为用户embedding，将用户的身份信息embedding 为一个低维的向量，从而表征用户的影响力信息；第二部分为路径编码，使用循环神经网络 (Recurrent Neural Network, RNN) 生成每一条传播路径的向量表示；第三部分为结合时间衰减的加和池化，使用监督学习得到不同时间的衰减系数，然后将每一条路径的向量表示与相应的衰减系数相乘后进行带权加和池化，得到传播图的向量表示。最后，利用一个多层感知机从传播图的向量表示得到对于未来转发次数的预测。下面我们对每一个部分进行简要介绍。

 

 

用户embedding

为了得到每一个用户身份信息的embedding, DeepHawkes 使用了监督学习的方法，每一个用户被表示为一个的 one-hot 向量，其中 N 为用户的总数。所有 N 个用户共享一个 embedding matrix， 其中 K 为一个可调节的参数，代表 embedding 的维度。这个embedding matrix把每一个用户转化为一个空间内的向量表示：

注意embedding矩阵 在将在整个神经网络的训练过程中通过监督学习来获得。

 

路径编码

 

在获得了用户的embedding 向量后，DeepHawkes使用RNN来编码每一条传播路径。具体来说，DeepHawkes使用一个GRU (Gate Recurrent Unit)[2]，第k 个隐状态 (hidden state) 计算如下：

复位门 (reset gate)：

其中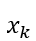为路径上第k个用户的embedding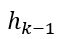，为第k-1个隐状态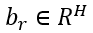，，,为参数矩阵, σ(∙) 表示sigmoid 函数。

更新门 (update gate):

其中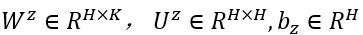 

隐状态：

其中

⨀表示逐个元素相乘 (element-wise product)，,,

最终的隐状态将作为该路径的向量表示。所有路径的向量表示将在下一个步骤被加权求和来得到传播图的向量表示，这体现了Hawkes过程的自激励机制，即每一次转发都会提高该信息在未来被转发的概率。

 

时间衰减

一次转发的影响力会随着时间的流逝而下降，为了模拟这一过程，DeepHawkes将观察窗口(0，T] 切分为L个等长的片段，每一个片段对应一个衰减系数 . 对于一个时间为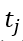的转发 (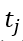为该转发距离该信息第一次发布，即0时刻的时间差)，其对应的衰减系数为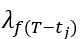， 其中

每一条传播路径对应的衰减系数由该路径上最后一次转发的时间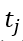决定。最终传播图的向量表示为

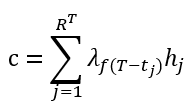
其中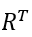为路径总数。

 

输出层

输出层为一个多层感知机（multi-layer perceptron）,以传播图的向量表示 c 为输入，输出观察窗口结束时刻 T 之后还会有多少次转发。整个神经网络的目标函数为

其中 M 为训练集中传M播图总数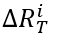，为第 i 个传播图在观察窗口结束时刻T之后的转发次数，为神经网络预测的次数。训练过程中，以最小化此目标函数为目的进行参数优化。

 

CasCN:

CasCN 来自于2019年ICDE论文《Information Diffusion Prediction via Recurrent Cascades Convolution》[3]，其思想与DeepHawkes类似，都利用了自激励机制和时间衰减机制，其与DeepHawkes的主要区别在于产生传播图的向量表示的过程中，使用了GCN（图卷积神经网络）来更好地提取传播图的拓扑结构信息，其网络结构如下图：

子图序列的抽取

与DeepHawkes不同，CasCN将传播图组织为一个的子图序列（sub-cascade graphsequence） 而非传播路径。序列包含一系列的子图 , 第一个子图只包含信息起始点，之后的每一个子图相比上一个子图增加一条转发。下图为一示例：

 

时序与拓扑模型

与DeepHawkes相同，CasCN使用RNN来保存传播图的时序特征，但不同点在于，CasCN的RNN是基于子图序列而非传播路径的，同时，它使用了GCN来提取传播图的拓扑结构。具体来说，它用Defferards graph convNet [4]中的图卷积操作替代了LSTM (long short-term memory) [5]中的矩阵乘法操作。LSTM的每一层接受子图序列中一个子图的邻接矩阵作为输入信号，结合上一层的隐状态 (hidden state)和细胞状态 (cell state), 计算本层的hidden state 和 cell state.

第t层的各个门状态如下：

其中表示以为参数矩阵，基于传播图的拉普拉斯矩阵的图卷积操作。在这步操作中有一些技术点，例如有向图的拉普拉斯矩阵的计算，使用切比雪夫展开来降低计算代价等，论文中有一章节进行详细介绍，具体操作在此不做过多叙述。W,U,V,b为不同的参数矩阵。

最终该层的隐状态 (hidden state)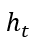和细胞状态 (cell state) 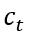如下所示：

 

 

时间衰减与最终输出

CasCN使用的时间衰减机制与DeepHawkes相同，最终传播图的向量表示为

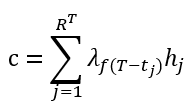
为观察窗口内信息转发的总次数，为LSTM第j层的隐状态，到第 j 次转发为止的子图序列都被编码在了这个隐状态中， 为第j次转发的时间， 为对应的衰减系数，定义和DeepHawkes 相同，也是通过监督学习获得的。

 

之后，CasCN 同样使用多层感知机预测T之后还会有多少次转发，并使用和DeepHawkes相同的目标函数，在此不作赘述。

 

实验对比

下图实验节选自CasCN论文，实验使用的数据集分别为新浪微博的微博转发数据集 (Weibo Dataset) 和论文开源网站 arXiv 上的论文引用数据集(HEP-PH)，M 代表不同的方法，而 T 则表示观察窗口的大小。实验使用 mean square log-transformed error （MSLE）作为准确率指标

P 为测试集大小，为第 i 个传播图在观察窗口之后增加的转发次数，为神经网络预测的次数。MSLE的计算方式与两种算法的目标函数相同。从图中我们可以看出，DeepHawkes 与CasCN 具有目前最好的预测效果，CasCN精度要高于DeepHawkes。

 

参考文献

 

[1].   Cao Q, Shen H, Cen K, et al.Deephawkes: Bridging the gap between prediction and understanding ofinformation cascades[C]//Proceedings of the 2017 ACM on Conference onInformation and Knowledge Management. 2017: 1149-1158.

[2].    Cho, Kyunghyun, et al."Learning Phrase Representations using RNN Encoder–Decoder for StatisticalMachine Translation." Empirical methods in natural language processing,2014, 1724-1734

[3].    Chen, Xueqin, et al."Information diffusion prediction via recurrent cascadesconvolution." 2019 IEEE 35th International Conference on DataEngineering (ICDE). IEEE, 2019.

[4].    Defferrard, Michaël, XavierBresson, and Pierre Vandergheynst. "Convolutional neural networks ongraphs with fast localized spectral filtering." Advances in neuralinformation processing systems. 2016.

[5].     Hochreiter, Sepp, and JürgenSchmidhuber. "Long short-term memory." Neural computation 9.8(1997): 1735-1780.