TetGen - Tetrahedral Generator

TetGen是一款四面体网格生成器。它创建多面体域的三维三角剖分。它能生成具有良好形状的单元网格，单元大小适合于几何特征或用户提供的尺寸函数。它在科学计算的各种应用中都有应用，如计算机图形学(CG)、计算机辅助设计(CAD)、几何处理(参数化和计算机动画)和物理模拟(有限元分析)。

TetGen的功能

对于一组3d(加权)点，TetGen生成Delaunay和 weighted Delaunay四面体网格以及它们的对偶，Voronoi图和幂图。
对于三维多面体域，TetGen生成 constrained Delaunay四面体网格及其各向同性自适应四面体网格。域边界(边缘和面)被尊重，并能在结果网格中被保留。

所得到的四面体的形状可以被证明是适合于大量输入的。它的主要应用之一是用有限元和有限体积法等数值方法来模拟物理现象。良好的网格质量是实现高精度和高效率模拟的关键。

TetGen的算法是基于Delaunay的。它们可以保存任意复杂的几何形状和拓扑结构。TetGen使用了一种constrained Delaunay优化算法，保证了网格划分的终止以及良好的网格质量。TetGen的鲁棒性通过使用计算几何中发展的先进技术得到了增强。一篇技术论文描述了TetGen中使用的算法和技术，可以在[1]中找到。

TetGen是由魏尔斯特拉斯应用分析和随机学研究所(WIAS)支持的一个长期研究项目的成果。它是不断发展和改进的。

TetGen是用C++编写的。它使用标准的C/ C++库。它很容易在所有主要的32位和64位计算机系统上编译和运行。TetGen的源代码可以在TetGen: A Quality Tetrahedral Mesh Generator免费获得。它是根据GNU Affero General Public License(AGPL) (v 3.0或更高版本)或WIAS提供的商业许可证的条款发布的。

本节的其余部分将简要描述TetGen中考虑的三角剖分和网格划分问题，并概述实现的算法。对于TetGen的基本使用，大多数信息都不是必须知道的，但是章节1.2.1和1.2.5包含了一些必要的指导方针，以创建正确的输入和生成高质量的四面体网格。

[1] H. Si. TetGen, towards a quality tetrahedral mesh generator. WIAS Preprint No. 1762, 2013. submitted to ACM TOMS.

点集的三角剖分

三角形是基本的几何结构。Rd上的点集V的三角剖分是一个d维单纯复形S，它的顶点集是V的子集或等于V。S的下空间是V的凸包。给定一个点集，它有许多三角剖分。其中，Delaunay三角剖分法是最有趣的一种。Delaunay三角剖分的对偶是点集的Voronoi图。Delaunay三角剖分和Voronoi图有许多很好的数学性质。它们被广泛应用于许多领域。

（1） Delaunay三角剖分，Voronoi图

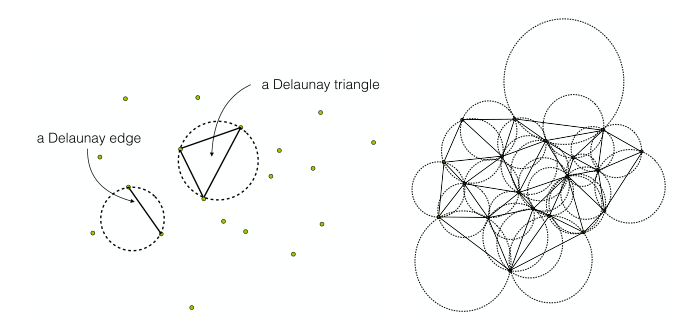
设V是Rd中的点集，σ是一个k-单纯形(0≤k≤d)，其顶点在V中。σ的圆周是一个球体，它穿过σ的所有顶点。如果k = d，则σ有一个唯一的环，否则，则σ有无穷多个环。如果σ存在一个圆，且圆内没有V的顶点，则σ为Delaunay，见下图左。

V的Delaunay三角剖分D是一个单纯复形，所有的单纯复形都是Delaunay，D的底空间是V的凸包。下图右示二维Delaunay三角剖分。三维Delaunay三角剖分也称为Delaunay四面体剖分。

如果V中没有d+2点在公共球面上，则V处于一般位置。否则，我们说V处于特殊的位置(或V是退化的)。当V处于一般位置时，V的Delaunay三角剖分是唯一的。可以通过对V中的点的坐标施加任意的小扰动来消除退化。

Delaunay三角形的对偶图是Voronoi图(见下图)。对于任何顶点p∈V，p的Voronoi单元是到p的距离不大于到V的任何其他顶点的距离的点集合，即集合cell(p) = {x∈Rd;||x−p||≤||x−q||，∀q∈V}，其中||·||为欧氏距离。V的Voronoi图是Rd的一个细分，分为Voronoi单元(其中一些可能是无界的)和它们的面。它是一个d维多面体复合形。如果点集V在一般位置，则Delaunay三角的k-simplices与Voronoi图的(d - k)-polyhedra是一一对应的，其中0≤k≤d。在R3，Voronoi图的顶点是Delaunay四面体化的四面体的圆心。

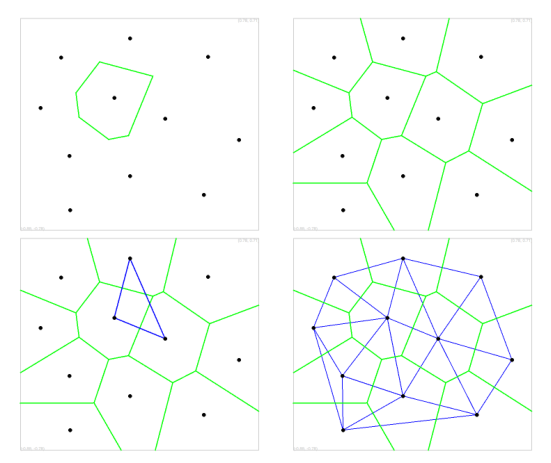
（2）加权Delaunay三角剖分，幂图

加权Delaunay三角剖分是Delaunay三角剖分的一种推广，它用“加权距离”代替了欧几里得距离。我们将每个点p∈Rd关联到一个权值(一个实数值)wp∈R。带权重的点称为Rd × R中的加权点。特别地，Rd中的点可以被认为是权值为零的加权点。

将一个点的权值写成非负实数的平方很方便，这里p≥0，wp =±p2。加权点p´= (p，±p2)可以理解为以p为中心，半径为p的球体。下图(左)显示了R2中的一组加权点。

两个加权点p´和z´之间的加权距离为：

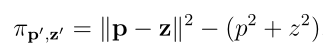
两个加权点p´和z´，若加权距离为0，则它们正交，即:

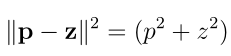
当两个加权点的加权距离为正时，我们说它们远于正交；当它们的加权距离为虚数时，我们说它们近于正交。

一般来说，Rd上的d+1个点定义了一个通过它们的唯一外接球。同样，Rd中的d + 1个加权点定义了一个唯一的公共正交球。当所有点的权值都为0时，它们的正交球就是它们的外接球。下图(右)给出了二维中三个加权点的正交球的例子。

令V´⊂Rd × R是加权点的有限集。我们说一个球是空的，如果V´中的所有加权点都远于它的正交。V´的加权Delaunay三角剖分是一个单纯复形D´，使得每个单纯形都有一个空的正交球，D´的底空间是V´的凸包。显然，如果所有点权重相同，加权Delaunay三角剖分与通常的Delaunay三角剖分是一样的。注意，加权Delaunay三角剖分并不一定包含V´中的所有点。

加权Delaunay三角剖分的对偶是加权Voronoi图，也称为加权点集V´的幂图。幂图也可以类似地使用加权距离代替欧氏距离定义为Voronoi图。如果V´中没有d + 2个加权点共用一个正交球，即处于一般位置，则加权Delaunay三角剖分的单纯形与幂图中的单元有一一对应关系。在R3中，幂图的顶点是加权Delaunay四面体化的四面体的垂心。

（3）算法

生成Delaunay(和加权Delaunay)四面体化的算法在计算几何中得到了很好的研究。TetGen实现了两种算法，Bowyer-Watson算法和增量翻转算法。两种算法都是递增的，即依次插入点。它们的最坏情况运行时间都是O(n2)在大多数实际应用中，它们通常是非常有效的。例如，如果点均匀分布，则期望运行时间为O(n log n)。

增量算法的速度很大程度上受点定位代价的影响。TetGen使用了一个空间排序方案来改进点的位置。其思想是对这些点进行排序，使空间中相邻的点具有相邻的指标。这些点首先被随机分成不同的组，然后每组中的点沿着希尔伯特曲线排序。按这个顺序插入点，每个点的位置可以在几乎恒定的时间内完成。

TetGen使用Shewchuk的精确几何谓词来执行Orient3D、InSphere和Orient4D测试。这足以保证生成Delaunay和加权Delaunay四面体化的数值鲁棒性。TetGen使用简化的象征性的扰动方案来消除退化。

CGAL 5.4 - 3D Triangulations Packages

CGAL的基本三维三角剖分类主要用于表示R3中一组点A的三角剖分。它是将A的凸包分割成顶点为A中点的四面体。与以凸包边界为边界的无界单元一起，三角剖分形成。它的单元(3-faces)是这样的：两个单元格要么不相交，要么共享一个共同的facet(2-face)、边缘(1-face)或顶点(0-face)。

一、表示

为了只处理四面体，这样的处理方便许多应用，可以将无界单元细分为四面体，考虑每个凸包面都与一个无限单元关联，无限单元的第四个顶点为一个辅助顶点，称为无限顶点。这样，每个面恰好与两个单元有关，凸包边界上的特殊情况易于处理。

CGAL的Triangulation_3类实现了这个观点，因此认为点集的三角化是一组有限的和无限的四面体。请注意，无限顶点没有有效的坐标，并且不能对其应用任何几何谓词。

三角剖分是通过关联关系和邻接关系连接在一起的顶点和单元的集合。每个单元可以访问它的四个关联顶点和它的四个相邻单元。每个顶点都可以访问它的一个关联单元。

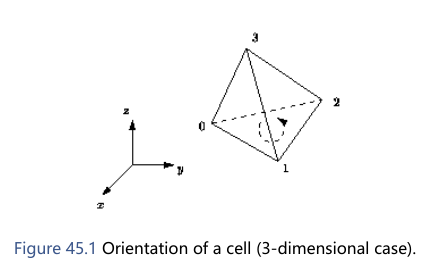
单元的四个顶点以正方向0、1、2和3为索引，正方向由底层欧氏空间的方向定义（见图45.1）。单元的邻居也用0、1、2、3进行索引，指标为 i 的邻居与具有相同指标的顶点相对。

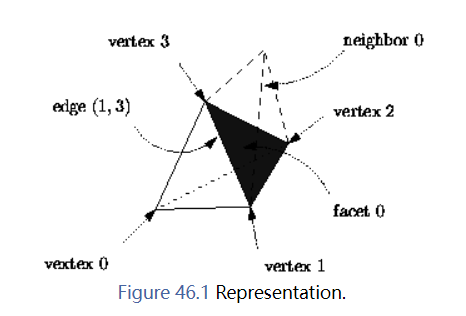
在底层的组合三角剖分（见3D三角剖分数据结构）中，边(1-faces)和面(2-faces)不是显式表示的：面是由单元和一个指标给出（单元c的i面是与顶点i相对的单元c的一个面），边是由单元和两个指标给出（单元c的边(i, j)是以c的顶点i和j为端点的边）,见图46.1。

（一）维度退化

类Triangulation_3也可以处理维度小于3的三角剖分。Rd点集的三角剖分覆盖了整个Rd空间，由具有d+1个顶点的单元组成：其中一些是无限的，它们是通过连接附加的无限顶点到凸包的每个面来获得的。

维度2：当一个三角剖分只包含共面点（即只有三个点的情况）时，它由三角形面组成。

维度1：三角剖分只包含共线点（只有两点的情况下），由边组成。

维度0：三角剖分只包含一个有限点。

维度-1：这是一种处理三角剖分的唯一顶点是无限顶点的情况的惯例。

在所有情况下都使用相同的单元类：二维中的三角形面可以被认为是退化单元，只有三个顶点（或者视邻居情况而定）编号（0，1，2）；一维中的边只有两个顶点（或者视邻居情况而定）编号0和1。

对于退化维度（即维度<3）面的隐式表示（视各边情况而定）仍然成立：在二维，每个单元仅有一个3指标的面和3条边（0,1），（1,2）和（2,0）；在一维，每个单元仅有一条边（0,1）。

（二）有效性

满足以下条件，则称R3的三角剖分是局部有效的：

(a)-(b) 它的底层组合图，三角剖分数据结构是局部有效的（见3D三角剖分数据结构章节的引言)

(c)任何单元的顶点都是按照正方向排列的，参见图45.1。

当三角剖分退化为维数为2的三角剖分时，其几何有效条件退化为:

(c-2D)对于任意两个有共同边（u，v）的相邻三角形（u，v，w1）和（u，v，w2)，在平面内，w1和w2位于（u，v）的两侧。

当所有点共线时，这个条件变为:

(c-1D)对于任意两条相邻边（u，v）和（u，w），在直线上，u和w位于公共顶点v的两侧。

方法Triangulation_3::is_valid()检查给定三角剖分的本地有效性。这并不总是确保全局有效性，但对于实际情况来说已经足够了。

二、Delaunay三角剖分

类Delaunay_triangulation_3表示三维Delaunay三角剖分。Delaunay三角剖分具有特定的空球性质，即该三角剖分的每个单元的外接球内部不包含该三角剖分的任何其他顶点。这些三角形的定义是唯一的，除了在退化的情况下，其中五个点是共球面。但是请注意，即使在这些情况下，CGAL实现也会计算唯一的三角测量。这个实现是完全动态的：它支持点的插入、顶点的移除和点的位移。