提词宝:快速保存Facebook视频教程
目标人群与痛点
目标人群:经常在Facebook上浏览视频但不知道如何保存的用户,包括学生、内容创作者、营销从业者,以及需要保存重要视频素材的人。
痛点与场景:
- 看到喜欢的视频,担心视频被删除或下架却无法保存。
- 想要下载Facebook上的教学视频、营销案例或灵感素材,却找不到方便的工具。
- 普通下载工具复杂繁琐,或者需要安装额外插件,用户体验不佳。
解决方案:提词宝通过内置的**一键下载视频**功能,快速解析Facebook视频链接并下载到本地,无需繁琐操作,让用户高效保存重要视频内容。

操作步骤
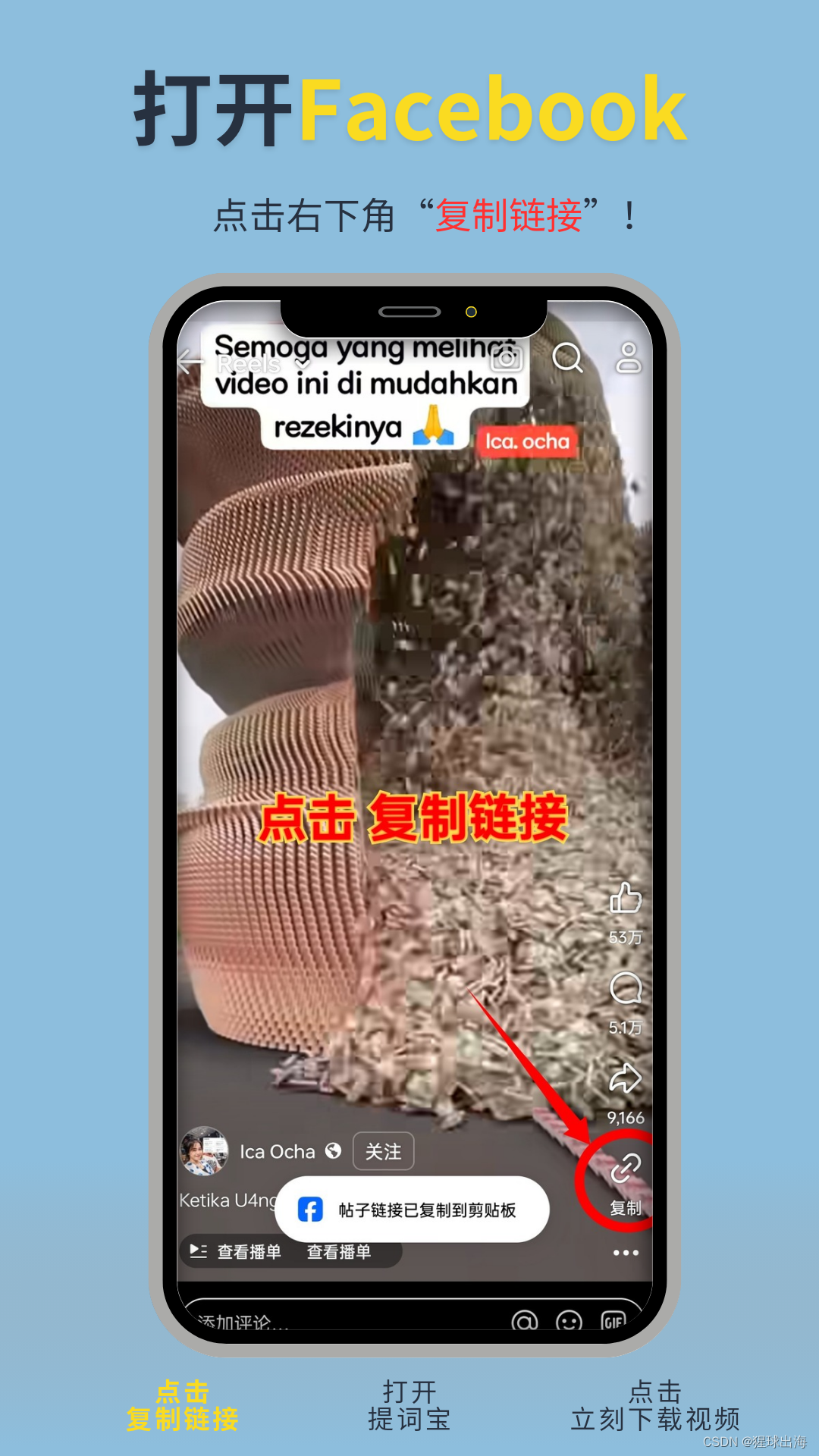
1. 复制Facebook视频链接
在Facebook中找到你需要下载的视频,按照以下步骤操作:
- 点击视频右上角的“更多选项”按钮。
- 选择“复制链接”,将视频链接保存到剪贴板。
2. 打开提词宝
启动提词宝App,并进入主界面。
- 在主界面选择“视频工具”模块。
- 点击“下载视频”选项。
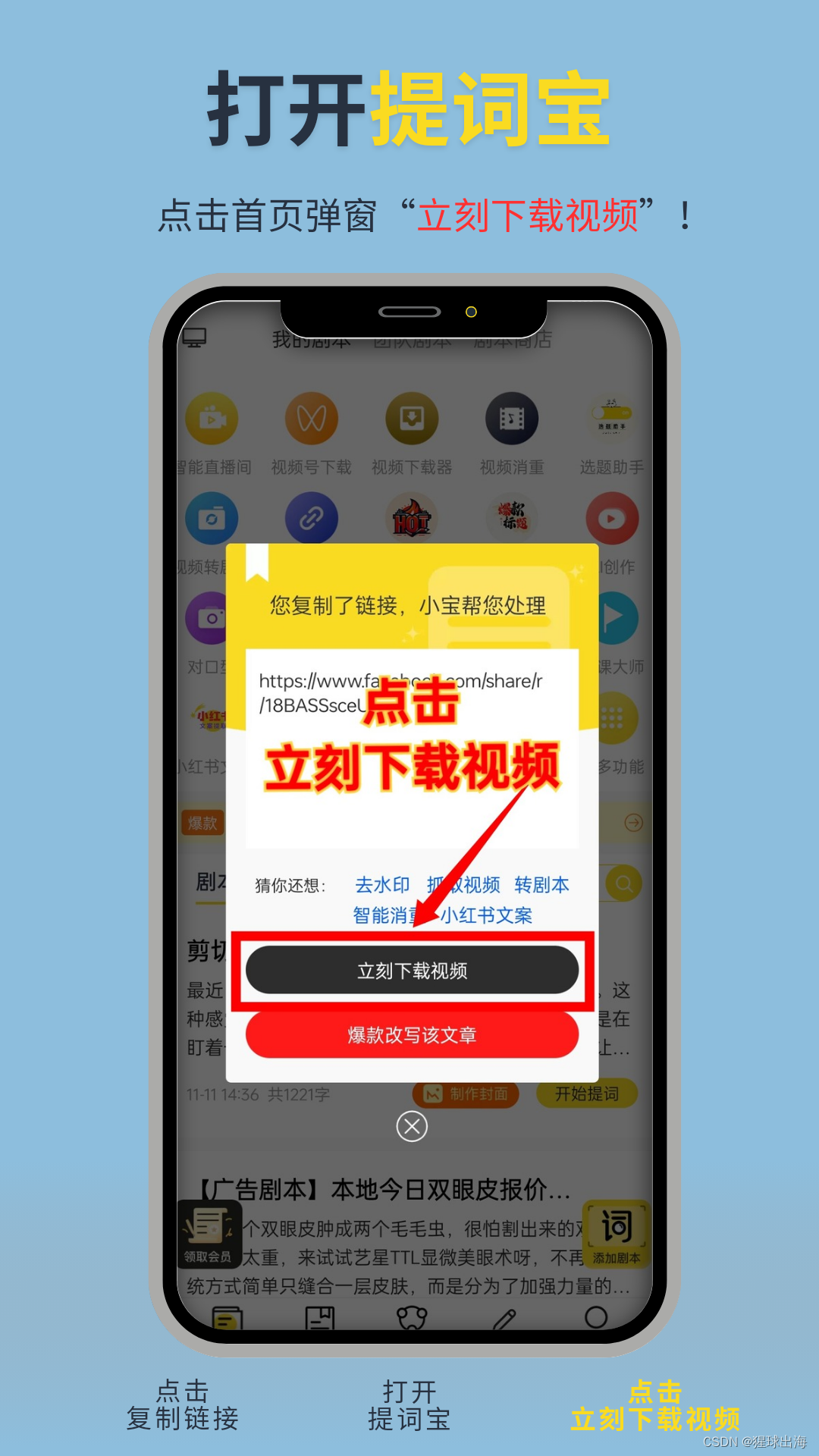
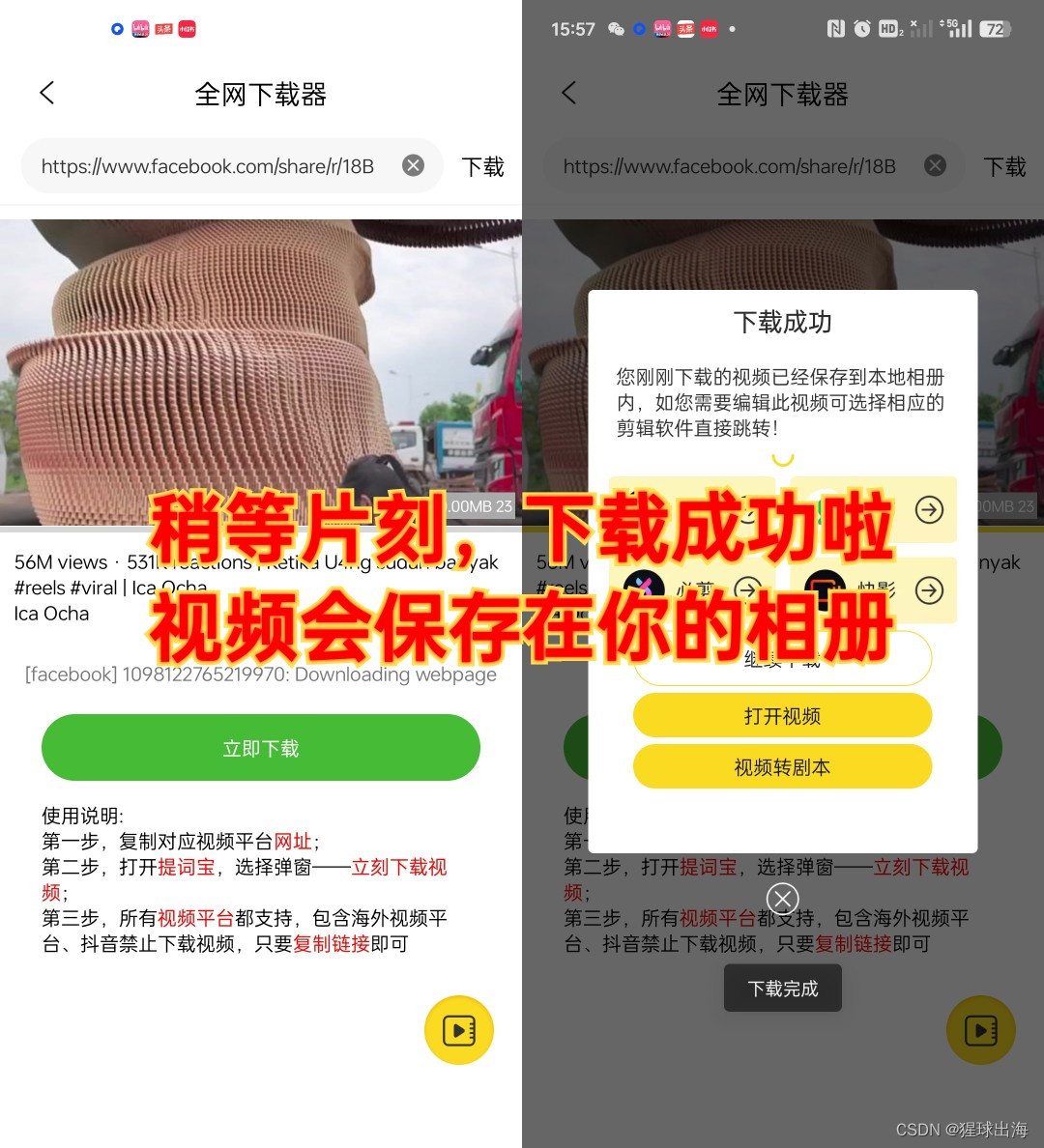
3. 粘贴链接并开始下载
提词宝会自动检测剪贴板内容,并弹出“立刻下载视频”的窗口。如果未弹出,请手动粘贴刚才复制的Facebook视频链接。
点击“立刻下载视频”按钮,稍等片刻,系统会自动解析并开始下载视频。
4. 下载完成
下载完成后,视频会自动保存到设备的本地文件夹。你可以在“下载记录”中查看并管理已保存的视频。
注意事项
- 确保视频的隐私设置允许下载,否则可能解析失败。
- 下载的视频仅限个人使用,勿用于商业用途或未经许可的传播。
- 建议在稳定的网络环境下操作,避免解析失败。
支持与帮助
如有任何问题,可通过以下找团队:
ticibao001