数据结构考研考点（持续更新）

一、绪论

1、数据元素是数据的基本单位，一个数据元素可以由若干数据项组成，数据项是构成数据元素的不可分割的最小单位。

2、数据结构是数据元素与数据元素之间的关系。

3、数据结构三要素：逻辑结构：独立于计算机（线性<1对1：栈、队列>、非线性<树、图、堆、散列表/哈希表）；存储结构/物理结构：逻辑结构在计算机中的存储形式（顺序存储；链式存储；索引存储；散列存储/哈希存储）。

4、在决定某种数据结构选取何种存储形式时，需要重点考虑的是：需要支持哪些运算。

5、 抽象数据类型包含：数据对象、逻辑关系、数据操作。

6、算法时间复杂度：某算法的时间复杂度为O(n²)，表明该算法执行时间与n²成正比。

最小的是最好的：O(1)<O(logn)<O(n)<O(nlogn)<O(n³)<O( $2^{n}$ )<O(n!)<O( $n^{n}$ ) (常对幂指)

二、线性表

1、线性表在频繁读写数据的时候适合采用顺序存储；只允许在线性表的一端进行读写操作、需要频繁在表中插入和删除数据的时候适合采用链式存储；

2、顺序表

既支持顺序存取，又支持随机存取，存储密度高；大片连续空间分配，改进容量时不方便。

插入：

最坏：插到表头，i=1，移动次数为n，O(n)

最好：插到表尾，i=表长+1，移动次数为0，O(1)

平均：插入任何一个位置等概率情况下，平均移动次数n/2，O(n)

删除：

最坏：删除表头，i=1，移动次数为n-1，O(n)

最好：删除表尾，i=表长，移动次数为0，O(1)

平均：删除任何一个元素等概率情况下，平均移动次数(n-1)/2，O(n)

查找：

最坏：目标元素在表尾，需要移动n元素，O(n)

最好：目标元素在表头，O(1)

平均：目标元素出现在任何一个位置的概率，概率都相同，为(n+1)/2，O(n)

3、在一个含n个元素的有序线性表上进行二分查找，找一个元素最多需要比较（log2n下取整+1 / log2(n+1)上取整）次。

4、链表

不可随机存取，只能顺序存取，存储密度低；离散的小空间分配，改进容量时方便。

5、单链表

尾插：r->next=p,r=p

头插：p->next=L->next,L->next=p

指定节点前面插入：s->next=p->next,p->next=s

6、双链表

插入：将s插到p后面

①s->next=p->next;

②p->next->prior=s;

③s->prior=p;

④p->next=s;

上面的顺序不是唯一的，也可以是③①②④，但①必须在④之前。

删除：删除p

先让要删除节点的前驱的后指针指向要删除节点的后继，再让要删除节点的后继的前指针指向要删除节点的前驱

①p->prior->next=q->next;

②p->next->prior=p->prior;

7、循环链表

循环单链表：p->next=Head //p是尾结点，指向头节点

(单链表：p->next=NULL）

循环单链表为空：Head->next=Head

循环双链表：p->next=Head && Head->prior=p

(双链表：p->next=NULL）

循环双链表为空：Head->next=Head

三、栈和队列

1、栈和队列都是特殊的线性表，都是插入删除受约束的线性表。

2、栈：先进后出

n个不同元素进栈，出栈的排序顺序有 $C_{2n}^{n}$ /(n+1)，3个就有5种。

栈空：top==-1；栈满：top==maxsize-1；栈长：top+1

进栈：指针先加1，再入栈；出栈：先出栈，指针再减1

一个栈的输入序列为1，2，3，……，n，若输出序列第一个元素为i，则输出的第j个元素是不确定

3、队列：先进先出

循环队列（插入时，队尾后移）：队空：rear=front；队满：front=(rear+1)%maxsize；队长：(rear-front+maxsize)%maxsize；入队：先入队，后指针加1；出队：直接front+1（front始终指向队头元素）

链式队列：只能尾进头出；队空：front和rera都指向头结点

双端队列：两端均可操作

4、栈的括号匹配

每出现一个右括号，就消耗一个栈顶左括号，否则入栈。

5、表达式求值

中缀表达式：a+b

前缀表达式（波兰式）：+ab

后缀表达式（逆波兰）：ab+ 每扫描到一个运算符就取出栈顶两个数计算变为一个数再放进去

中缀转后缀（手算）：a+b*（c-d）-e/f

①加括号：（（a+（b*（c-d）））-（e/f））

②运算符后移：（（a（b（cd）-）*）+（ef）/）-

③去除括号：abcd-*+ef/-

中缀转后缀（机算）：扫描中缀表达式，遇到操作数直接加入表达式；遇到左括号直接入栈，右括号依次弹出栈内运算符，直到弹出左括号；遇到运算符：依次弹出栈中优先级高于或等于当前运算符的所有运算符，并加入后缀表达式。

中缀表达式的计算（两个算法的结合）：扫描到操作数，入运算符栈；扫到运算符或者界限符，入运算符栈，弹出元素同上；没弹出一个运算符就用操作数栈的栈顶两个元素做相应运算，得到结果后再放回操作数栈。

详细操作可见(王道408考研数据结构)第三章栈和队列-第三节1：栈的应用之括号匹配问题和表达式问题（前缀、中缀和后缀）_王道考研中缀-CSDN博客

6、函数调用：最后被调用的函数最先执行结束

7、递归中的调用：每进入一层递归，就将递归调用所需信息压入栈顶，每退出一层递归，就从栈顶弹出相应信息。

递归：将一个问题划分为子问题解决，然后再把子问题划分为更小的问题，直至划分到不能再划分为止（自上而下解决问题）。

8、队列应用：层次遍历；图的广度优先便利；FCFC（先来先服务）

9、数组和邻接矩阵

请参考下面的文章：

(王道408考研数据结构)第三章栈和队列-第四节：特殊矩阵压缩方式_三对角矩阵在王道哪一章-CSDN博客

四、树与二叉树

1、结点数=总度数+1

2、度为m的树第i层至多有 $m^{i-1}$ 个结点（i≥1）

3、高度为h的m叉树至少有h个结点；高度为h度为m的树至少有h+m-1个结点。（因为度为m的树至少有一个结点的度为m；而m叉树允许所有结点的度都小于m）

4、n个结点的m叉树的最小高度：

5、特殊的二叉树

满二叉树：不存在度为1的结点；结点总数： $2^{h}$ -1

完全二叉树：最多只有一个度为1的结点

二叉排序树（线索二叉树）：左<根<右

平衡二叉树：树上任一结点的左子树和右子树的高度之差不超过1

6、非空二叉树中，叶结点数=度为2的结点数+1

7、二叉树第i层至多有 $2^{i-1}$ 个结点

8、高度为h的二叉树至多有 $2^{h}$ -1个结点（也就是满二叉树）

9、具有n个节点的完全二叉树的高度

10、完全二叉树：第i个结点的双亲结点为；i≤时该结点为分支节点，i≥时该结点为叶结点。

11、二叉树的存储结构：顺序存储（只适合完全二叉树）；链式存储（最常用）

12、二叉树的遍历：

先序：根左右

中序：左根右

后序：左右根

层次遍历（队列）：自上而下一层一层的

13、树的存储结构

双亲表示法

孩子表示法

（将每个结点的孩子结点排列起来，以单链表作为存储结构）

孩子兄弟表示法

（设置两个指针，分别指向该结点的第一个孩子和此结点的右兄弟）

14、树、森林与二叉树的转换

15、树和森林的遍历

树的遍历：

先序遍历:ABEFIGCDHJKLNOM

后序遍历:EIFGBCJKNOLMHDA

层次遍历:ABCDEFGHIJKLMNO

森林遍历同理！

16、哈夫曼树/霍夫曼树

（每次选最小的两个结合起来）

霍夫曼树（符号数量大于1）的结点数一定是奇数

霍夫曼编码

17、二叉排序树（BST）

左小右大，中序遍历是一个递增序列

查找：如果相等，那么查找成功；如果小于，则在左子树上继续查找；如果大于，则在右子树上继续查找

插入：从根节点出发，对比关键字

构造：按照序列依次插入

删除：叶子节点直接删除；只有左子树或者右子树，直接让其子树代替；左右子树均有，用左子树的最左节点（即右子树中最小的结点）或者右子树最左节点（即左子树中最大的结点）替代。

18、优先队列（堆）

最大优先队列：无论入队顺序如何，都是最大元素出队

优先队列的实现常选用二叉堆，在数据结构中，优先队列一般也是指堆。

堆就是一颗完全二叉树，这颗完全二叉树有这样一个特点：它的结点要么大于任意一个孩子结点，要么小于任意一个孩子结点

如果其结点大于任意一个孩子结点，就称其为大顶堆，此时其最大的结点是根节点；

如果其结点小于任意一个孩子结点，就称其为小顶堆，此时其最小的结点是根节点。

左图大顶堆，右图小顶堆：

五、图

1、线性表可以是空表，树可以是空树，但图不可以是空图。边e可以是空的，此时表明两个顶点v没有关系。

2、基本概念

有向图：图G中的每条边都是有方向的;

无向图：图G中的每条边都是无方向的;

完全图：图G任意两个顶点都有一条边相连接;

无向完全图

任意两个顶点之间都存在边， n个顶点的无向图有 n(n-1)/2 条边；

有向完全图

任意两个顶点之间都存在方向互为相反的两条边，n个顶点的有向图有n(n-1)条边；

简单图、多重图：若不存在顶点到其自身的边，且同一条边不重复出现，则称这样的图为简单图，反之则为多重图；

稀疏图：边很少；稠密图：边很多；

子图：

带权图：边上带权的图其中权是指每条边可以标上具有某种含义的数值(即与边相关的数)；

网络：=带权图；

连通图

在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与v2是连通的。如果图中任意一对顶点都是连通的，则称此图是连通图。连通图最少有n-1条边；非连通图最多有 $C_{n-1}^{2}$ 条边；

n个结点的无向图至少需要n-1条边才能确保它是连通图。

非连通图的极大连通子图叫做连通分量；

强连通图

在有向图中，若对于每一对顶点vi和vj，都存在一条从vi到vj和从vj到vi的路径，则称此图是强连通图；强连通图最少有n条边；

非强连通图的极大强连通子图叫做强连通分量；

邻接点：若(u，v)是E(G)中的一条边，则称u与v互为邻接顶点

弧头和尾：有向边(u，v)称为弧，边的始点u叫弧尾，终点v叫弧头

度、入度和出度：顶点v的度是与它相关联的边的条数。记作TD(v)。在有向图中，顶点的度等于该顶点的入度与出度之和。顶点v的入度是以v为终点的有向边的条数，记作ID(v)；顶点v的出度是以v为始点的有向边的条数，记作 OD(v)。 //以第一视觉第一人称分入度出度

无向图中边数其实就是各顶点度数和的一半

（当有向图中仅1个顶点的入度为0，其余顶点的入度均为1，此时，是树的形状，有向树）

生成树

是一个极小连通子图，它含有图中全部顶点，但只有n-1条边；

如果在生成树上添加1条边，必定构成一个环。

若图中有n个顶点，却少于n-1条边，必为非连通图。

生成森林

由若干棵生成树组成，含全部顶点，但构成这些树的边是最少的。

路径长度：非带权图的路径长度是指此路径上边的条数；带权图的路径长度是指路径上各边的权之和。

简单路径：路径上各顶点 v1,v2,...,vm 均不互相重复

回路：若路径上第一个顶点 v1 与最后一个顶点vm 重合，则称这样的路径为回路或环

3、图的存储结构（图的实现）

邻接矩阵-数组表示法（存稠密图）

含n个顶点和e条边的有向简单图的邻接矩阵中，0元素的个数： $n^{_{2}}$ -e

含n个顶点和e条边的无向简单图的邻接矩阵中，0元素的个数： $n^{_{2}}$ -2e

邻接表-链式表示法（存稀疏图）

十字链表（有向图）

邻接多重表（只适用于无向图）

3、图的遍历

广度优先(BFS)

在访问了起始点v之后，依次访问 v的邻接点；然后再依次访问这些顶点中未被访问过的邻接点；直到所有顶点都被访问过为止。

基本思想——仿树的层次遍历——用队列（出队时，访问与队头相邻的顶点，未被访问过的顶点入队）

时间复杂度：O(v+e)；空间复杂度O(n)

深度优先(DFS)

访问起始点 v；若v的第1个邻接点没访问过，深度遍历此邻接点；若当前邻接点已访问过，再找v的第2个邻接点重新遍历。

基本思想——仿树的前序遍历——用递归

时间复杂度：O(v+e)；空间复杂度O(n)

详情参考下面的文章：

(王道408考研数据结构)第六章图-第三节：图的遍历(DFS和BFS)_王道数据结构中bfs，从1出发调用几次？-CSDN博客

求生成树可以用DFS，也可以用BFS；求最大连通分量只能用DFS。

4、最小生成树

一个连通图的生成树是一个极小的连通子图，它含有最小生成树：图中全部的n个顶点，但是却只有足以组成一棵树的n-1条边。对于网来说，各个边具有权值，因此我们把这个极小连通子图形成的最小代价树称之为最小生成树。主要有以下两种算法:

Prim

加点，适用于稠密图，采用邻接矩阵作为图的存储表示；O（n2）

Kruskal

加边，适用于稀疏图，采用邻接表作为图的存储表示。O（elog2e）

5、最短路径

Dijkstra：单源最短路径。

//本质属于贪心算法

算法思想：先找出从源点v0到各终点vk的直达路径（v0,vk），即通过一条弧到达的路径。从这些路径中找出一条长度最短的路径（v0,u），然后对其余各条路径进行适当调整：若在图中存在弧（u,vk），且（v0,u）+（u,vk）<（v0,vk），则以路径（v0,u,vk）代替（v0,vk）。在调整后的各条路径中，再找长度最短的路径，依此类推。总之，按路径“长度” 递增的次序来逐步产生最短路径

dist[ ]数组：存储了当前起点到其余顶点最短路径的长度

path[ ]数组：存储了起点到其余顶点的最短路径(通过查询该数组Q，可获得路径信息)

final[ ]数组：如果标记为1则表示该顶点被选入最短路径

一遍一遍刷新三个数组，每一轮确定final为false的结点中dist最小的那个（下次就可以将其作为中转的点）

时间复杂度：O( $v^{2}$ )；空间复杂度：O(v)

详情可参考下面的文章：

(王道408考研数据结构)第六章图-第四节4：最短路径之迪杰斯特拉算法（思想、代码、演示、答题规范）_迪杰斯特拉算法王道-CSDN博客

Floyd：所有顶点间的最短路径

//动态规划

A[ ][ ]：用来记录当前已经求得的任意两个顶点最短路径的长度

path[ ]：来记录当前两顶点间最短路径上要经过的中间顶点

多重for循环，路径数组、path数组每一轮都增加一个新的点作为中转结点，扫描二维数组的路径值，替换成小的那个值。

时间复杂度：O( $v^{3}$ )；空间复杂度：O( $v^{2}$ )

详情可参考下面的文章：

(王道408考研数据结构)第六章图-第四节5：最短路径之弗洛伊德算法（思想、代码、演示、答题规范）_弗洛伊德算法王道-CSDN博客

BFS：无权图单源

while循环嵌套一个for循环：其实，while循环控制一层一层往下走，for循环控制从左到右每一层遍历。

6、拓扑排序

算法思想：用一个数组纪录图G的每个顶点的入度；找出第一个入度为0的点输出；找出与之相连的所有顶点，将他们的入度都减1；重复操作，直至没有入度为0的点。

拓扑排序：将入度为0的点逐个删除；

逆拓扑排序：先出出度为0的结点，可用DFS实现

7、关键路径

我们把路径上各个活动的持续时间之和称之为路径长度。从源点到终点具有最大长度的路径叫做关键路径，在关键路径上的活动叫做关键活动。关键路径直接决定了整个工程的时间长短，有缩短关键路径上的关键活动时间才能减少整个工程时间。

最早发生时间和最晚发生时间相同的活动为关键活动。

六、查找

1、线性查找

顺序查找

逐一比较 O(n)

折半查找

先排序，再二分。（单链表无法实现）O(log2n)

二分查找判定树

找到有序表中任一记录的过程就是：走了一条从根结点到与该记录对应结点的路径。

比较的关键字个数为：该结点在判定树上的层次数。

查找成功时比较的关键字个数最多不超过树的深度

查找不成功的过程就是：走了一条从根结点到外部结点的路径。

分块查找

使其块内无序，块间有序

（块间折半，块内线性）对索引表进行折半查找。若在索引表内找到，则到对应的块内顺序查找；若查找失败，则在low对应的块内顺序查找，如果还找不到，则数组中没有这个元素。

效率分析：假设n个记录被平均分成了m块，每个块中有t条记录，也即t=n/m。再假设 $_{}$ $L_{b}$ 为查找索引表的平均查找长度，因最好与最差等概率元素，所以设 $L_{b}$ 的平均长度为(m+1)/2；设 $L_{w}$ 为块中查找记录的平均查找长度，同理有 $L_{w}$ =(t+1)/2
于是分块查找的平均查找长度为：ASL= $L_{b}$ + $L_{w}$ =
从上面的式子可以看到，结果取决于数据集四的总记录数n和每个记录数。

其最佳情况就是分的块数m与块中记录数n相同，此时就有n=m*t=t*t，因此ASL= $^{\sqrt{n}}$ +1

2、散列表（哈希表）

建立关键码字与其存储位置的对应关系，或者说，由关键码的值决定数据的存储地址。 理想情况下，查找速度极快（O(1)），查找效率与元素个数n无关！

哈希函数：在元素与其存储位置之间唯一确定一对应关系f，称之为哈希函数。使得每个关键字key对应一个存储位置f(key)。

若把所有记录存储在一块连续的空间上，那么这样的结构就称之为哈希表，关键字对应的存储位置则称之为哈希地址。

冲突：通常关键码的集合比哈希地址集合大得多，因而经过哈希函数变换后，可能将不同的关键码映射到同一个哈希地址上，这种现象称为冲突。（在哈希查找方法中，冲突是不可能避免的，只能尽可能减少）

哈希函数的构造方法

直接定址法（适合关键字的分布基本基本连续的）

Hash(key) = a*key + b (a、b为常数)

优点：以关键码key的某个线性函数值为哈希地址，不会产生冲突。

缺点：要占用连续地址空间，空间效率低。

除留余数法

Hash(key)=key % p (p是一个整数)

特点：以关键码除以p的余数作为哈希地址。

关键：如何选取合适的p？若设计的哈希表长为m，则一般取p≤m且为质数

数字分析法

特点：选用关键字的某几位组合成哈希地址。选用原则应当是：各种符号在该位上出现的频率大致相同。

平方取中法

特点：对关键码平方后，按哈希表大小，取中间的若干位作为哈希地址。

理由：因为中间几位与数据的每一位都相关。

例：2589的平方值为6702921，可以取中间的029为地址。

总之，构造哈希函数的原则：

① 执行速度（即计算哈希函数所需时间）；

② 关键字的长度；

③ 哈希表的大小；

④ 关键字的分布情况；

⑤ 查找频率。

冲突处理方法

开放定址法（线性探测法；平方探测；双散列法；伪随机探测）

设计思路：有冲突时就去寻找下一个空的哈希地址，只要哈希表足够大，空的哈希地址总能找到，并将数据元素存入。

A、线性探测法

（往后一个）：Hi=(Hash(key)+di) mod m ( 1≤i < m )

B、平方探测

注：若di＝伪随机序列，就称为伪随机探测法

拉链法（即链表）

基本思想：将具有相同哈希地址的记录链成一个单链表，m个哈希地址就设m个单链表，然后用一个数组将m个单链表的表头指针存储起来，形成一个动态的结构。

性能分析：散列函数、装填因子α、冲突处理方法

α=表中装填的记录数 / 哈希表的长度

α越大，表中记录数越多，说明表装得越满，发生冲突的可能性就越大，查找时比较次数就越多。

3、树型查找（线索二叉树/二叉排序树）

七、排序

1、排序的基本概念

排序：将一组杂乱无章的数据按一定的规律顺次排列起来。排序的目的：便于查找

时间效率——排序速度（即排序所花费的全部比较次数）

空间效率——占内存辅助空间的大小

稳定性——若两个记录A和B的关键字值相等，但排序后A、B的先后次序保持不变，则称这种排序算法是稳定的。

内部排序：若待排序记录都在内存中，称为内部排序

内部排序的算法：插入排序；交换排序（重点是快速排序）；选择排序；归并排序；基数排序

2、插入排序（直接插入排序、折半插入排序、希尔排序）

插入排序的基本思想：每步将一个待排序的对象，按其关键码大小，插入到前面已经排好序的一组对象的适当位置上，直到对象全部插入为止。

直接插入排序：时间：O(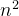 $n^{2}$ ) 空间：O(1) 稳定

折半插入排序（优化——比较次数大大减少，全部元素比较次数仅为O(nlog2n)。）

既然子表有序且为顺序存储结构，则插入时采用折半查找定可加速。

时间：O( $n^{2}$ ) 虽然比较次数大大减少，可惜移动次数并未减少，所以排序效率仍为O( $n^{2}$ )

空间：O(1)

稳定

希尔排序：时间：O( $n^{_{1.25}}$ )～O(1.6 $n^{_{1.25}}$ )；空间：O(1) 不稳定

先将整个待排记录序列分割成若干子序列,分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

步骤说明：

dk=5的时候，

1	2	3	4	5	1	2	3	4	5
49	38	65	97	76	13	27	49*	55	04

序号相同的进行排序：

1	2	3	4	5	1	2	3	4	5
13	27	49*	55	04	49	38	65	97	76

dk=3的时候，

1	2	3	1	2	3	1	2	3	1
13	27	49*	55	04	49	38	65	97	76

序号相同的进行排序：

1	2	3	1	2	3	1	2	3	1
13	04	49*	38	27	49	55	65	97	76

dk=1的时候，

1	1	1	1	1	1	1	1	1	1
13	04	49*	38	27	49	55	65	97	76

序号相同的进行排序：

1	1	1	1	1	1	1	1	1	1
04	13	27	38	49*	49	55	65	76	97

3、交换排序（冒泡排序、快速排序）

交换排序的基本思想：两两比较待排序记录的关键码，如果发生逆序（即排列顺序与排序后的次序正好相反），则交换之，直到所有记录都排好序为止。

冒泡排序：时间：O(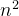 $n^{2}$ ) 空间：O(1) 稳定

每趟不断将记录两两比较，并按“前小后大”（或“前大后小”）规则交换。

快速排序：时间：O(nlog2n) 空间：O(log2n) 不稳定

从待排序列中任取一个元素 (例如取第一个) 作为中心，所有比它小的元素一律前放，所有比它大的元素一律后放，形成左右两个子表；然后再对各子表重新选择中心元素并依此规则调整，直到每个子表的元素只剩一个。此时便为有序序列了。

一般情况下，快速排序的平均时间复杂度最低

4、选择排序（简单选择、堆排序）

选择排序的基本思想是：每一趟在后面n-i 个待排记录中选取关键字最小的记录作为有序序列中的第i 个记录。

简单选择：时间：O(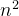 $n^{2}$ ) 空间：O(1) 不稳定

每经过一趟比较就找出一个最小值，与待排序列最前面的位置互换即可

堆排序：时间：O(nlog2n) 空间：O(1) 不稳定

优点：对小文件效果不明显，但对大文件有效。

什么是堆？

堆就是一颗完全二叉树，这颗完全二叉树有这样一个特点：它的结点要么大于任意一个孩子结点，要么小于任意一个孩子结点

如果其结点大于任意一个孩子结点，就称其为大顶堆，此时其最大的结点是根节点；

如果其结点小于任意一个孩子结点，就称其为小顶堆，此时其最小的结点是根节点。

左图大顶堆，右图小顶堆：

怎样建堆？

从最后一个非终端结点开始往前逐步调整，让每个双亲大于（或小于）子女，直到根结点为止。

怎样堆排序？

每一次将最上面的元素与最下面的元素互换，并对目前的顶点进行调整，使其满足要求，最终得到从小到大的顺序序列。

堆的插入和删除

插入（向上调整）：放到尾部，不满足要求，则将插入元素与父结点交换

删除：叶子节点直接删除；分支节点，用尾部结点代替原结点，然后调整成堆

5、归并排序

时间：O(nlog2n) 空间：O(n) 稳定

归并排序的基本思想是：将两个（或以上）的有序表组成新的有序表。分治法，递归

6、基数排序

基数排序的基本思想是：借助多关键字排序的思想对单逻辑关键字进行排序。即：用关键字不同的位值进行排序。最高位优先法MSD ，最低位优先法LSD

特点：不用比较和移动，改用分配和收集，时间效率高！

假设有n 个记录, 每个记录的关键字有d 位，每个关键字的取值有radix个, 则每趟分配需要的时间为O(n)，每趟收集需要的时间为O(radix)，合计每趟总时间为O (n+radix )

全部排序需要重复进行d 趟“分配”与“收集”。因此时间复杂度为：O ( d ( n+radix ) )

基数排序需要增加n+2radix个附加链接指针，空间效率低

空间复杂度：O(n+radix）

稳定性：稳定。(一直前后有序)。

用途：若基数radix相同，对于记录个数较多而关键码位数较少的情况，使用链式基数排序较好。

7、内部排序算法的比较及应用

八、算法

1、递归（分治）

Msater定理

相关知识参考链接：

算法时间复杂度详解_用分治法解决一个规模为n的问题。下列哪种方法是最慢的?-CSDN博客

【算法设计与分析】分治-时间复杂度计算_分治算法时间复杂度-CSDN博客