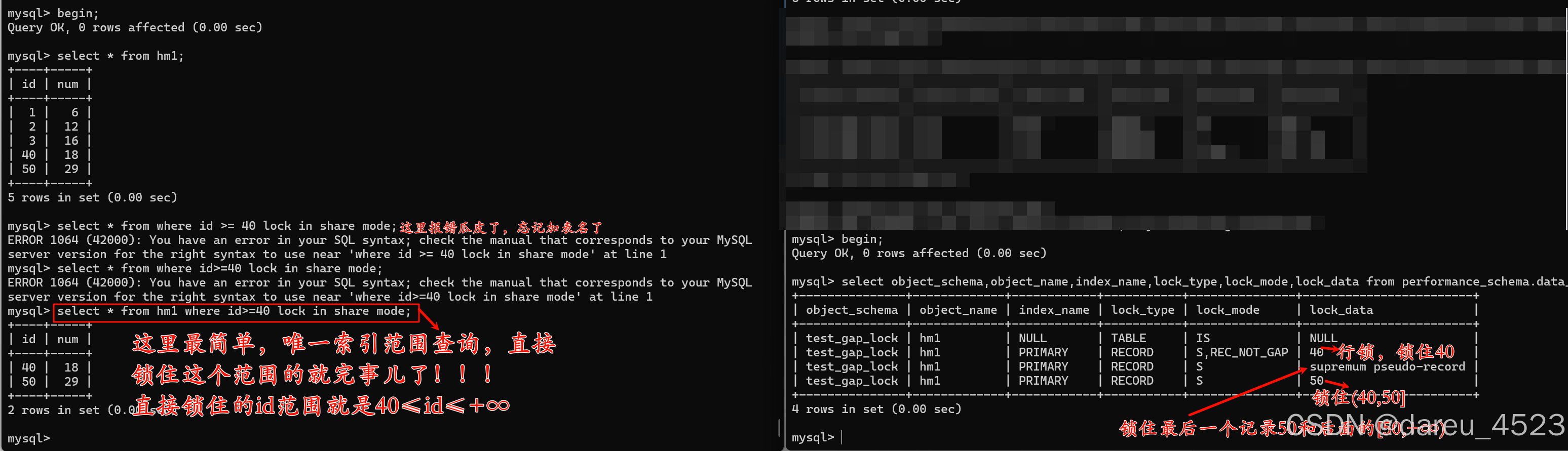
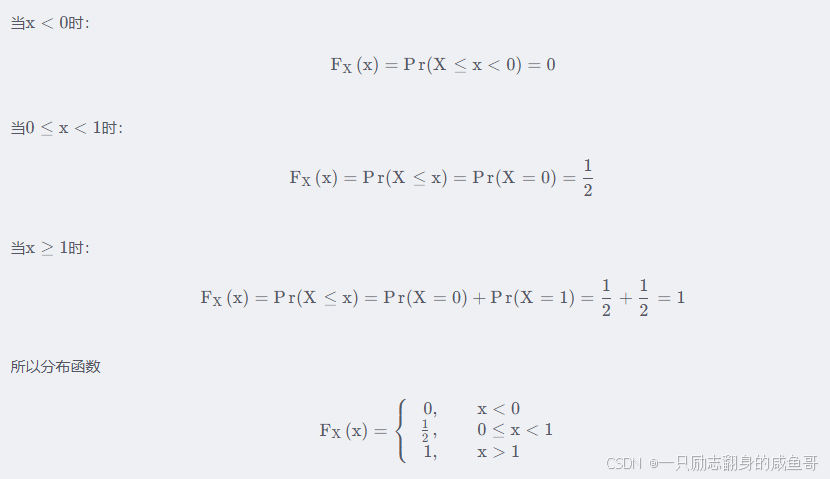34. 在排序数组中查找元素的第一个和最后一个位置二分法

34. 在排序数组中查找元素的第一个和最后一个位置

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {vector<int> res(2,-1);res[0]=findleft(nums,target);if(res[0] == -1) return res;res[1] = findright(nums,target);return res;}
private:int findleft(vector<int> &nums,int target){int left = 0,right = nums.size()-1, pos =-1;    while(left <= right){int mid = left + (right - left)/2;if(nums[mid] == target  ){//继续寻找左边相同的targetpos = mid;//存储最左边的相同值right =  mid-1;}else if(nums[mid] > target){right = mid-1;}else{left =mid+1;}}return pos;}int findright(vector<int> &nums,int target){int left = 0,right = nums.size()-1, pos =-1;    while(left <= right){int mid = left + (right - left)/2;if(nums[mid] == target  ){//继续寻找右边相同的targetpos = mid;//存储最右边的相同值left = mid +1;}else if(nums[mid] > target){right = mid-1;}else{left =mid+1;}}return pos;}};

在这道题中，分左右进行查找的核心原因是为了满足以下两个要求：

目标值在数组中的开始位置（最左边的位置）。
目标值在数组中的结束位置（最右边的位置）。

由于数组中可能存在多个相同的目标值 target，而普通的二分查找只能找到其中一个目标值，无法区分最左边还是最右边的位置。因此，我们必须 分两次二分查找 来解决这个问题。

为什么普通二分查找不够用？

假设数组为：

nums = {5, 7, 7, 8, 8, 10};
target = 8;

使用普通二分查找：

mid 可能落在第一个 8 处（索引 3），也可能落在第二个 8 处（索引 4）。
二分查找的默认逻辑在找到目标值后不确定要向左还是向右继续查找，导致只找到某个 target 的位置。

而题目要求：

最左位置：索引 3。
最右位置：索引 4。

分两次查找的必要性

为了确保找到 target 在数组中的起始位置和结束位置，必须使用以下两个独立的查找逻辑：

查找最左边的位置：
- 当找到 nums[mid] == target 时，不直接返回，而是继续向左查找（即 right = mid - 1）。
- 这样可以保证最终找到 target 出现的第一个位置。
查找最右边的位置：
- 当找到 nums[mid] == target 时，不直接返回，而是继续向右查找（即 left = mid + 1）。
- 这样可以保证最终找到 target 出现的最后一个位置。

分左右查找的实现原理

查找最左位置的过程：

当 nums[mid] == target：
- 记录当前位置 pos = mid（可能是最左的位置）。
- 向左继续搜索，即更新 right = mid - 1。
最终返回记录的 pos。

查找最右位置的过程：

当 nums[mid] == target：
- 记录当前位置 pos = mid（可能是最右的位置）。
- 向右继续搜索，即更新 left = mid + 1。
最终返回记录的 pos。

示例演示

假设 nums = {5, 7, 7, 8, 8, 10}，target = 8。

查找最左位置：

left = 0, right = 5, mid = 2 → nums[mid] = 7 < 8 → 更新 left = 3。
left = 3, right = 5, mid = 4 → nums[mid] = 8 → 更新 right = mid - 1 = 3。
left = 3, right = 3, mid = 3 → nums[mid] = 8 → 更新 right = mid - 1 = 2。

最终，最左位置是 3。

查找最右位置：

left = 0, right = 5, mid = 2 → nums[mid] = 7 < 8 → 更新 left = 3。
left = 3, right = 5, mid = 4 → nums[mid] = 8 → 更新 left = mid + 1 = 5。
left = 5, right = 5, mid = 5 → nums[mid] = 10 > 8 → 更新 right = mid - 1 = 4。

最终，最右位置是 4。

总结

为什么要分两次查找？
- 普通二分查找只能定位到某个 target，无法保证找到最左或最右位置。
- 分两次查找（向左、向右）可以准确找到开始和结束位置。
时间复杂度：
- 两次二分查找，每次都是 O(log⁡n)O(\log n)，总时间复杂度仍然是 O(log⁡n)O(\log n)。
代码清晰度：
- 通过两次独立查找，逻辑更清晰、易于理解。