== ！！！！！！导数公式表！！！！！！！！==

1.1 函数与反函数

1.1.1 y=f(x) x=g(y)互为反函数

在解反函数的题的时候，可以借助公式：（a+b)(a-b)=a²-b²。
eg:

1.2基本初等函数

1.2.1基本：不可再拆分，作为最基本的

基本函数如下：

1.3初等函数

1.3.1 初等函数定义

初等函数是由 常数、基本初等函数 经过 四则运算、符合运算 组成的式子。

1.4初等特性

1.4.1 有界性。

1.4.2 单调性

1.4.3 奇偶性 定义域要关于左右原点对称

1.4.3.1奇函数 f(-x)=-f(x)

1.4.3.2 偶函数 f(-x)=f(x)

1.4.4 周期性。注意一个可能会忽略的条件。x+T在定义域D内。

1.5极限

1.5.1

定义：无限接近，不一定会有取值，可能取到，可能取不到。

1.5.2去心邻域

定义：

1.6

主要思想就是分段函数，一定讨论左右极限值是否相等。从而判断左右极限是否存在。
设f(x)含…………，当x->b，一定分左右
eg:

1.7无穷小

疑问：无穷小是无穷小量吗？

1.7.1 无穷小的定义

用0做判断是因为0是撇开正负的无穷小。

0为什么是无穷小呢？1.是函数2.0的极限就是0.
注：如果是泛泛的问XXXX是否是无穷小，是要有条件的，是指明x0的。

1.7.2 无穷小之间的比较

1.8极限的性质

1.8.1 唯一性

极限一定只有一个

1.8.2 ！！！保号性！！！

1.8.2.1 保号性定义

1.8.2.2 保号性证明

1.8.2.3 例题

所以，左减右增，x为极小值。
1.8.3有界性
||a|-|b||<=|a-b|

有界不一定有极限。

1.8.4夹逼定理

数列性：

对应例题

1.9 N项和求极限

1.9.1 先求和后求极限

1.9.2 夹逼定理

注意：用夹逼定理的点在于分子或者是分母有一向是齐的另一个是不齐的。

1.9.3 定积分定义

注意：分子齐，分母齐， 分母多1次

题目里面那个看不懂的，是字母i。

1.10单调有界的数列必有极限

{An}有界<==> 存在上、下界
1）如果数列An是单调递增的，分为两种情况，一种是无上界，第二种是有上界。一定有下届。第一项为下界。
2）单调递减的数列，有上界，即第一项结果的值就是上界，不一定有下届。

1.11 极限的存在证明

1.11.1 例题

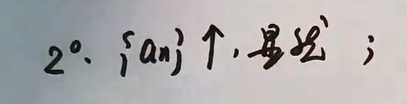
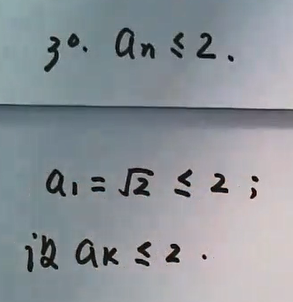
题目是为了证明An的极限存在。单调递增要证明有上界，单调递减要证明有下界？。
有4步。
1）数列的递增关系。
2）证明单调性和有界性。
3）因为是单调递增的，所以要考虑是否有上界，并进行证明（这个题目证明的是Ak,A(k+1)的关系。
4）求其极限。（3，4可合成一步）
例二：

在这个题目中，因为求出了下界即An+1>=1，所以下一步的解题思路是证明其递减。所以，极限存在。
例三
注：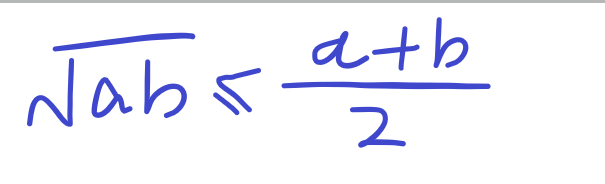

注意：在这个题中，不要理第一项。

1.13无穷小

1. 有限个无穷小：α是无穷小，β是无穷小 α＋β是无穷小、α×β是无穷小、α或β×常数k是无穷小常数
2. a有极限，b是无穷小，ab是无穷小。
3. == lim f(x)=A 等价于 f(x)=A+a,a是无穷小。！！！！！！！==

1.13.1 等价无穷小

无穷小和他自身是等价的
无穷小具有a=b <==> b=a
无穷小具有传递性 a=b b=c 得：a=c

1.13.2

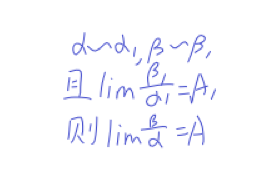
~代表等价关系。
当X趋近于0时，

1.14

两个重要极限
1）x>0,ln(1+x)<x
2)x>0,sinx<x
3)x!=0,ex>1+x，x是次幂
4）
重要极限：

🔺可以是个复杂的式子，也可以是简单的其他东西，但这里的一般应用都是x->0时的等式的替换如：lim(x->0)sinx/x=1.
== ！！！！！！！！！！型三：不定型极限！！！！！！！！！！！==

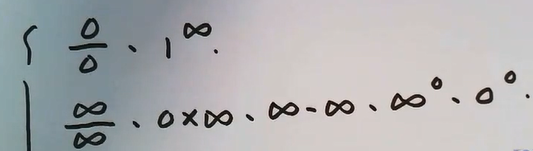
这里讲述的是零比零型，无穷比无穷型等。

x,sinx,tanx,arcsinx,arctanx,任意两者之差为3阶无穷小。
精确度：注意同阶问题。

三阶的精确度比一阶的要高，所以一阶的加减的精确度是不太行。但是乘除的可以放心等价？？？？？？为什么
例题：

这里注意是提取！但是不知道为什么，讲课的时候说的是精度不够。

这里是1的无穷次方的题型
这里的思路就是凑成（1+🔺）（1/🔺）次幂的形式。如下：。并且在凑的过程中要保持恒等变形。


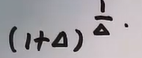
无穷比无穷型：

0×∞型：解题思路：转化为0比0型或者是∞比∞型。


∞-∞型：
1） 若有分母，则通分。
2） 没有分母，分子有理化。

答案写错了，是－1/3.

1.15 连续与间断

1.15.1 连续

注意：函数的极限和函数在这个点是否有定义域无关。
连续分为两种情况，第一个是在一个点上的连续。第二个在区间[a,b]上连续
在点a上连续：if lim(x->a)f(x)=f(a) <==> f(a-0)=f(a+0)=f(a)
在区间[a,b]上连续 if①f(x)在区间（a,b）内连续,即每一点处处都是连续的。
②f(a)=f(a+0)&&f(b)=f(b-0)。注：不考虑f(a-0)和f(b+0)
原因是因为取不到。

1.15.2 间段

if lim(x->a)f(x)!=f(a)
① f(a-0)=f(a+0)都存在。若 f(a-0)==f(a+0)则a为可去间断点
若 f(a-0) != f(a+0)则a为跳跃间断点
这两个是第一类间断点。
② f(a-0)=f(a+0)至少有一个不存在。则 为第二类间断点

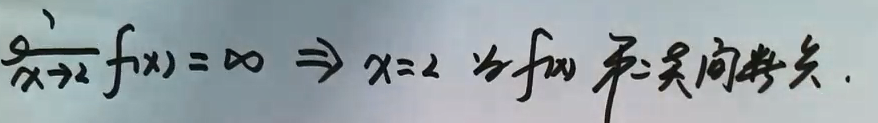
1.15.3