What I cannot create, I do not understand. - Richard Feynman
前言
你左拥右抱着 Stable Diffusion 和 MidJourney 创造美轮美奂的图片。
你熟练使用着 ChatGPT 和 LLaMa 创造辞致雅赡的文字。
你来回切换着 MuseNet 和 MuseGAN 创造高山流水的音乐。
毋庸置疑,人类最独特的能力就是创造,但在科技日新月异发展的今天,我们通过创建机器来创造!机器可以给定风格绘制原创艺术品 (draw),可以编写一长篇连贯文章 (write),可以创作悦耳的音乐 (compose),还可以为复杂游戏制定获胜策略 (play)。这个科技就是生成式人工智能 (Generative Artificial Intelligence, GenAI),现在只是 GenAI 革命的开始,现在是学习 GenAI 的最佳时机。
1. 生成和判别模型
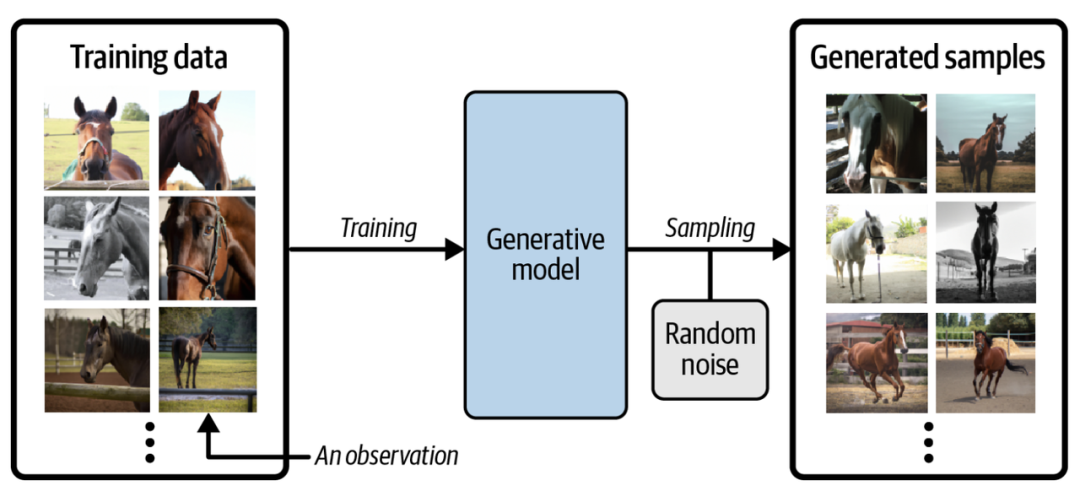
GenAI 是一个 buzzword,其背后本质是生成模型 (generative model),它是机器学习的一个分支,目标是训练模型以生成与给定数据集相似的新数据。
假设我们有一个马的数据集。首先,我们可以在此数据集上训练生成模型,以捕获控制马图像中像素之间复杂关系的规则。然后,从此模型中进行采样,以创建原始数据集中不存在的但是逼真的马图像,过程如下图所示。
为了真正理解生成模型的目标和重要性,将其与判别模型 (discriminative model) 进行比较是必要的。其实机器学习里大多数的问题都是由判别模型解决的,看以下例子。
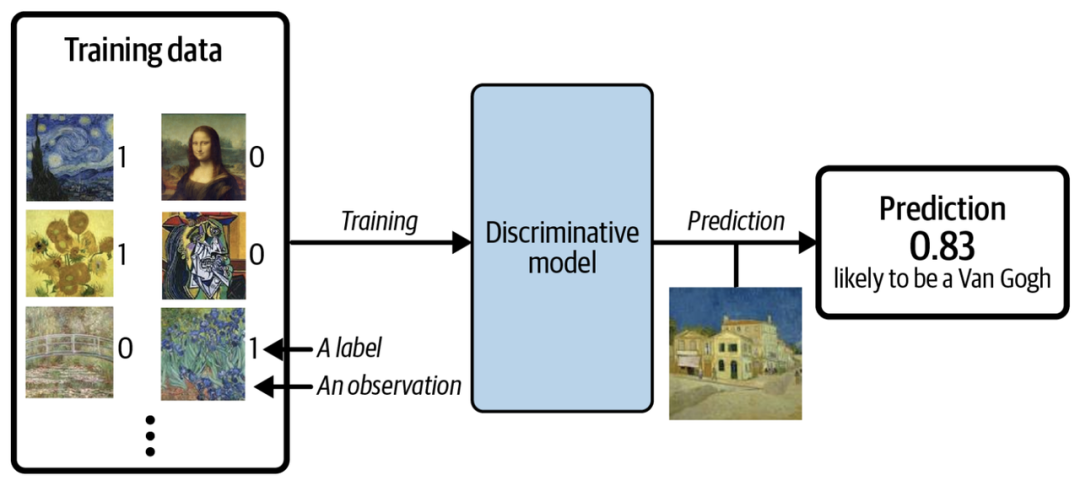
假设我们有一个绘画数据集,一些是梵高画的,一些是其他艺术家画的。有了足够的数据,我们就可以训练一个判别模型来预测一幅给定的画是否由梵高所作,过程如下图所示。
当使用判别模型时,训练集中每个示例都有一个标签 (label),对于以上二分类问题,通常梵高的画的标签为 1,非梵高的画的标签为 0。上图中模型最后预测的概率是 0.83,那么它很有可能是由梵高所作。和判别模型不同的是,生成模型不需要示例里含有标签,因为它的目标是生成新数据,而不是给数据预测标签。
例子看完,让我们用数学符号来精准定义生成模型和判别模型:
判别模型对 p(y|x) 建模,给定特征 x 来估计标签 y 的条件概率。
生成模型对 p(x) 建模,直接估计特征 x 的概率,从这个概率分布中采样即可生成新的特征。
需要注意的是,即使我们能够建立一个完美来识别梵高的画的判别模型,它仍然不知道如何创作一幅看起来像梵高的画,它只能输出一个概率,即图像是否来自梵高之手的可能性。由此可见,生成模型比判别模型要困难很多。
2. 生成模型的框架
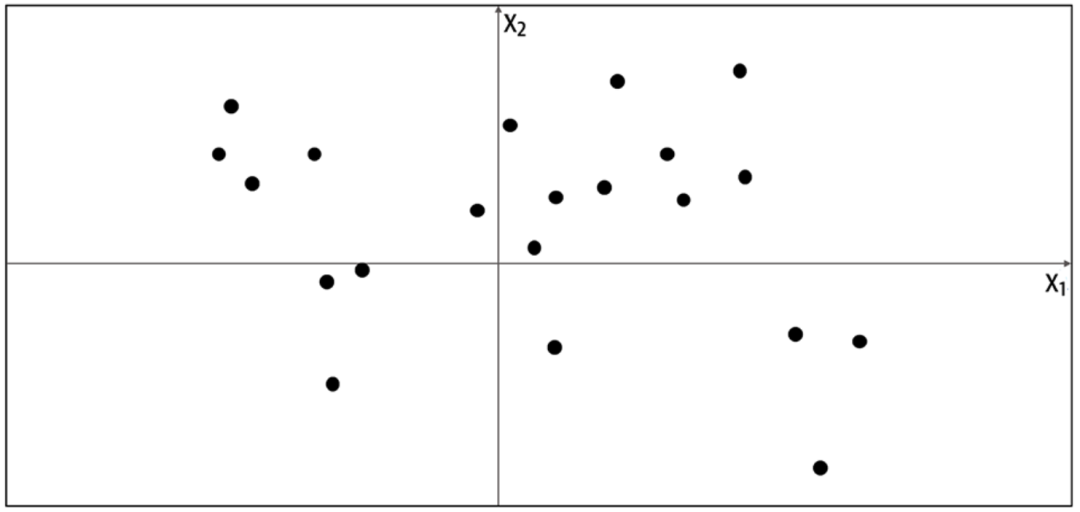
了解生成模型框架之前,让我们先玩一个游戏。假设下图的点是由某种规则产生,我们称该规则为 pdata,现在让你生成一个不同的 x = (x1, x2) 使得这个点看起来是由相同的规则 pdata 产生的。
你会如何生成这个点?你可能利用已给的点在脑海里产生一个模型 pmodel,而这个模型占的位置上都可能生成你想要的点。由此可知,模型 pmodel 就是 pdata 的估计。那么一个最简单的模型 pmodel 如下图的橙色方框,点只可能生成于方框内,而不可能生成于方框外。
要生成新的点,我们可以从方框内随机选一个点,更严谨地说,从模型 pmodel 分布中采样 (sampling)。这就是一个极简的生成模型。你从训练数据 (黑点) 中创建一个模型 (橙框),然后你可以从模型中采样,希望生成出来的点和训练集中的点看起来相似。
现在我们可以正式提出生成学习的框架了。
现在让我们揭示真实的数据生成分布 pdata,并了解如何应用以上框架于此示例。从下图中我们可以看到,数据生成规则 pdata 是点只是在陆地上均匀分布,而不会出现在海洋中。
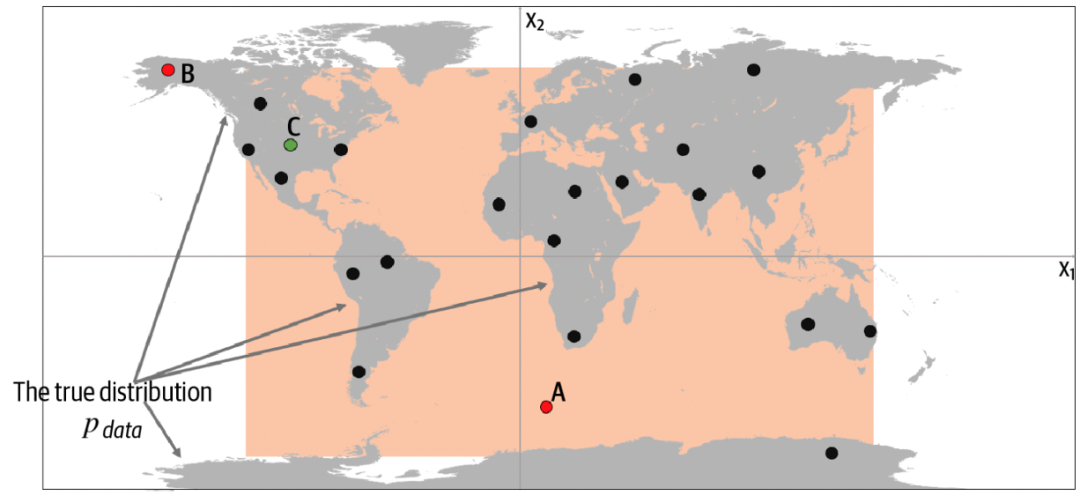
很明显,我们的模型 pmodel 是规则 pdata 的一个简化。通过检查上图的 A、B 和 C 点可以帮助我们理解模型 pmodel 是否成功模仿了规则 pdata。
点 A 不符合规则 pdata,因为它出现在海里,但可能由模型 pmodel 生成,因为它出现在橙框之内。
点 B 不可能由模型 pmodel 生成,因为它出现在橙框之外,但符合规则 pdata,因为它出现在陆地上。
点 C 由模型 pmodel 生成,而又符合规则 pdata。
这个例子展示了生成建模背后的基本概念,虽然现实中用生成模型要复杂很多,但其基本框架是相同。
3. 第一个生成模型
假设你是一家公司的首席时尚官 Chief Fashion Officer (CFO),你的职责是创造新的时髦的衣服。今年你收到 50 个关于时尚搭配的数据集 (如下图),而你需要创造 10 个新的时尚搭配。
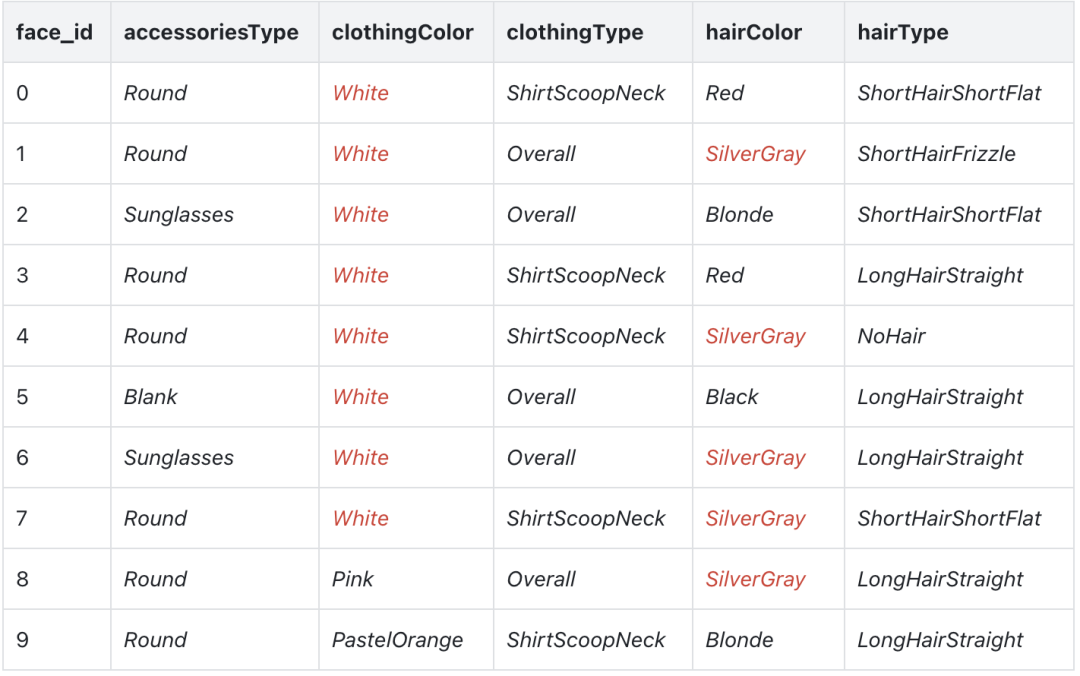
虽然你是首席时尚官,但是你也是一个数据科学家,因此你决定用生成模型来解决此问题。看完上面 50 张图片,你决定用五个特征,配件类型 (accessies type)、服装颜色 (clothing color)、服装类型 (clothing type)、头发颜色 (hair color) 和头发类型 (hair type),来描述时尚搭配。
前 10 个图像数据特征如下。
每个特征也有不同数目的特征值:
3 种配件类型 (accessories type):
Blank, Round, Sunglasses
8 种服装颜色 (clothing color):
Black, Blue01, Gray01, PastelGreen, PastelOrange, Pink, Red, White
4 种服装类型 (clothing type):
Hoodie, Overall, ShirtScoopNeck, ShirtVNeck
6 种头发颜色 (hair color) :
Black, Blonde, Brown, PastelPink, Red, SilverGray
7 种头发类型 (hair type):
NoHair, LongHairBun, LongHairCurly, LongHairStraight, ShortHairShortWaved, ShortHairShortFlat, ShortHairFrizzle
这样有 3 * 8 * 4 * 6 * 7 = 4032 种特征组合,所以可以想成样本空间里面包含着 4032 个点。从给出的 50 个数据点可以看出,pdata 对于不同特征会偏好某些特征值。从上表看出图像中白色服装颜色和银灰色头发颜色就比较多。由于我们不知道真实的 pdata,我们只能通过这 50 个数据来建一个 pmodel,使其能够和 pdata 相近。
3.1 极简模型
一个最简单的方法就是给 4032 个特征组合中每个点赋予一个概率参数,那么该模型包含 4031 个参数,因为所有概率参数加起来等于 1。现在我们来一个个检查 50 个数据,然后更新该模型的参数 (θ1, θ2, ...,θ4031),每个参数的表达式为:

其中 N 是观测数据的个数即 50,nj 是第 j 个特征组合在 50 个数据中出现的个数。
比如 (LongHairStraight, Red, Round, ShirtScoopNeck, White) 的特征组合 (称为组合 1) 出现了两次,那么

比如 (LongHairStraight, Red, Round, ShirtScoopNeck, Blue01) 的特征组合 (称为组合 2) 没有出现,那么
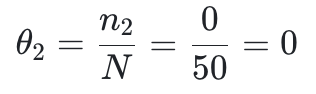
按照上面的规则,我们将 4031 个组合都计算出一个 θ 值,不难看出有很多 θ 值都是 0,更糟的是我们不可能生成新的没见过的图片 (θ = 0 意味着从未观测到拥有该特征组合的图片)。为了解决此问题,只需在分母加上特征数目的总数 d 和在分子加上 1,该技巧叫做拉普拉斯平滑。
现在,每个组合 (包括那些不在原始数据集中的组合) 都有非 0 的采样概率,然而这仍然不是一个令人满意的生成模型,因为不在原始数据集中的点的概率是一个常数。如果我们尝试使用这样的模型来生成梵高的画,那么它会以相同概率来操作一下两种画:
1. 梵高原作的复制画 (不在原始数据集)
2. 随机像素拼凑的画 (不在原始数据集)
这显然不是我们想要的生成模型,我们希望它能从数据中学到一些固有的结构,从而能够增加样本空间中它认为更有可能的区域的概率权重,而不是把所有概率权重放在数据集中存在的点上。
3.2 次简模型
朴素贝叶斯模型 (Naive Bayes) 可以将上面特征组合的次数大大减少,根据其模型假设每个特征之间都是相互独立的。回到上面的数据,一个人的头发颜色 (特征 xj) 和其衣服颜色 (特征 xk) 没有联系,用数学表达式表示就是:
有了这个假设,我们可以计算出
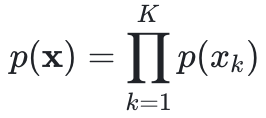
朴素贝叶斯模型将原始问题“对每个特征组合做概率估计”简化成对“每个特征做概率估计”,原来我们需要用 4031 (3 * 8 * 4 * 6 * 7) 个参数,现在只需要 23 (3 + 8 + 4 + 6 + 7) 个参数,每个参数的表达式为:
其中 N 是观测数据的个数即 50,nkl 是第 k 个特征取其下第 l 个特征值的个数。
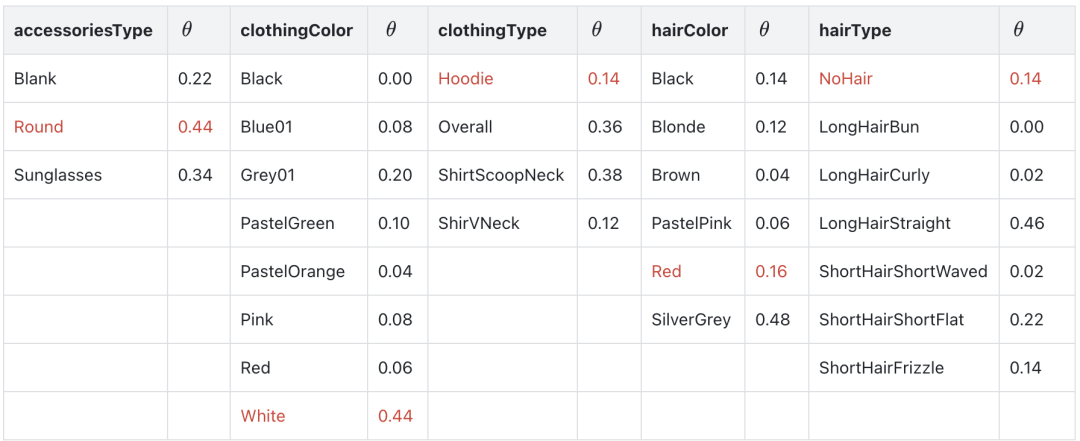
通过统计 50 个数据,下表给出朴素贝叶斯模型的参数值。
要计算模型生成某数据特征的概率,只需要连乘上表中的概率, 比如:
以上这个组合没有出现在原始数据集中,但模型仍然为它分配非零的概率,因此它仍然能够被模型生成。因此,朴素贝叶斯模型能够从数据中学习一些结构,并使用它来生成原始数据集中未见过的新示例。下图是模型生成的 10 张新的时尚搭配的图片。
在此问题中,特征只有 5 个属于低维数据,朴素贝叶斯模型假设它们相互独立还算是合理,因此模型生成的结果还不错,下面来看一个模型崩塌的例子。
4. 生成模型的难点
4.1 高维数据
作为首席时尚官,你成功用朴素贝叶斯生成了 10 套全新的时尚搭配,你信心爆棚了,觉得自己的模型无敌,直到遇到下面这套数据集。
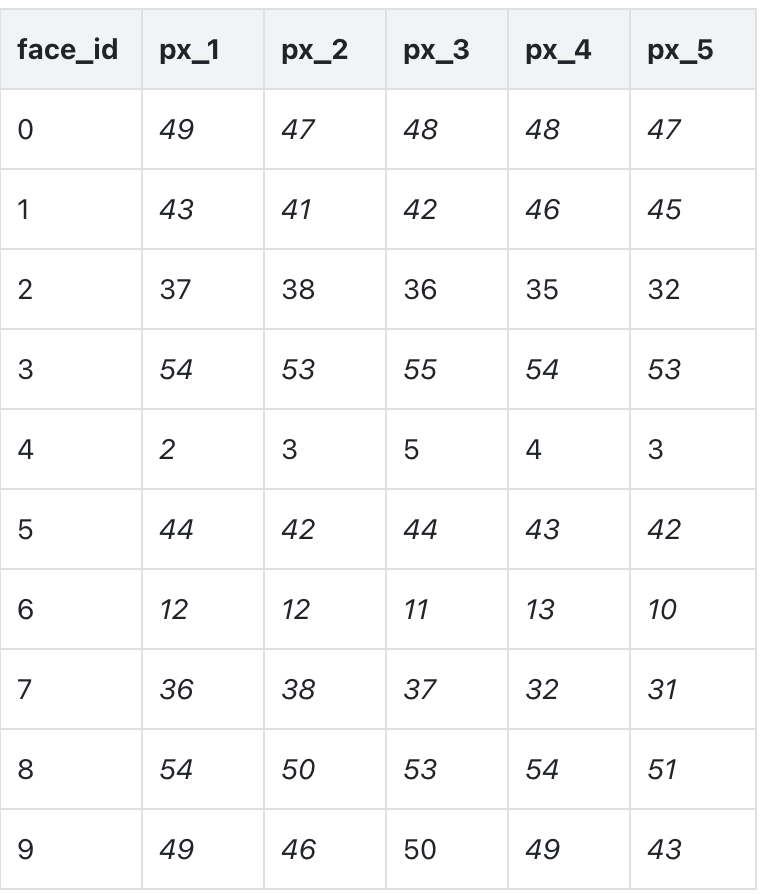
该数据集不再是用五个特征来表示了,而是由 32*32 = 1024 个像素来表示,每个像素值可以去 0 到 255 中的一个,0 表示白,255 表示黑。下表列出前 10 张图像像素 1 到 5 的值。
用同样的模型生成 10 套全新的时尚搭配,下面是模型生成的结果,每张丑得都很类似,而且无法区分不同的特征,为什么会这样呢?
首先,由于朴素贝叶斯模型是独立采样像素,但是相邻像素之间其实非常相似。对于衣服,其实像素应该大致相同,但是模型随机采样,因此得到上图中的衣服都是五颜六色的。其次,高维样本空间中的可能性太多,其中只有一小部分是可识别的。如果朴素贝叶斯模型直接处理这种高度相关的像素值,那么它找到令人满意的值组合的机会非常小。
综上所述,对于低维度而且特征低相关的样本空间,朴素贝叶斯效果通过独立采样的产生的效果很好;但对于高维度而且特征高相关的样本空间,通过独立采样像素来找到有效人脸几乎是不可能的。
这个例子强调了生成模型要想成功必须克服的两个难点:
模型如何处理高维特征之间的条件依赖关系?
模型如何从高维样本空间中找到满足条件的极小比例观察结果?
生成模型要想在高维度而且特征高相关的样本空间中成功,必须要利用深度学习模型。我们需要一个可以从数据中推断出相关结构的模型,而不是被告知要提前做出哪些假设。深度学习可以在低维空间中形成自己的特征,而这就是表征学习 (representation learning) 的一种形式。
4.2 表征学习
表征学习就是学习高维数据的表示的含义。
假设你去见一个从未见过面的网友,到达相约地点人很多根本找不到她,你打电话给她描述你的样子。相信你不会说你图像中像素 1 的颜色是黑,像素 2 的颜色是淡黑,像素 3 的颜色是灰等等。相反你会认为网友会对普通人的外貌有一个大概的了解,然后给予这个了解再描述像素组的特征,比如,你有一头乌黑亮丽的短发,戴着一双金光闪闪的眼镜等等。通常不超过 10 个这样的描述,网友就可以从脑海中生成你的图像,该图像可能很粗糙,但不妨碍网友从几百个人中找到你,即便她从来没有见过你。
这个就是表征学习背后的核心思想,不尝试直接对高维样本空间 (high-dimensional sample space) 进行建模,而是使用一些低维潜在空间 (low-dimensional latent space) 来描述训练集中的每个观察结果,然后学习一个映射函数 (mapping function),该函数可以获取潜在空间中的一个点并将其映射到原始样本空间。换句话说,潜在空间中的每个点都表示着高维数据的特征。
上面的话如果不好理解,请看下图由一些灰度罐子图像组成的训练集。
不难看出,这些罐子可以仅用两个特征来描述:高度和宽度。因此我们可以图像的高维像素空间转换成二维潜在空间,如下图所示。这样我们可以从潜在空间采样 (蓝点),然后通过映射函数 f 将其转换成图像。
认识到原始数据集可以用更简单的潜在空间来表示这件事情对于机器来说并不容易,首先机器需要确定高度和宽度是最能描述该数据集的两个潜在空间维度,然后学习映射函数 f 可以在这个空间中取一个点并将其映射到灰度罐图。深度学习使我们能够训练机器,使其无需人类指导即可找到这些复杂的关系。
5. 生成模型的分类
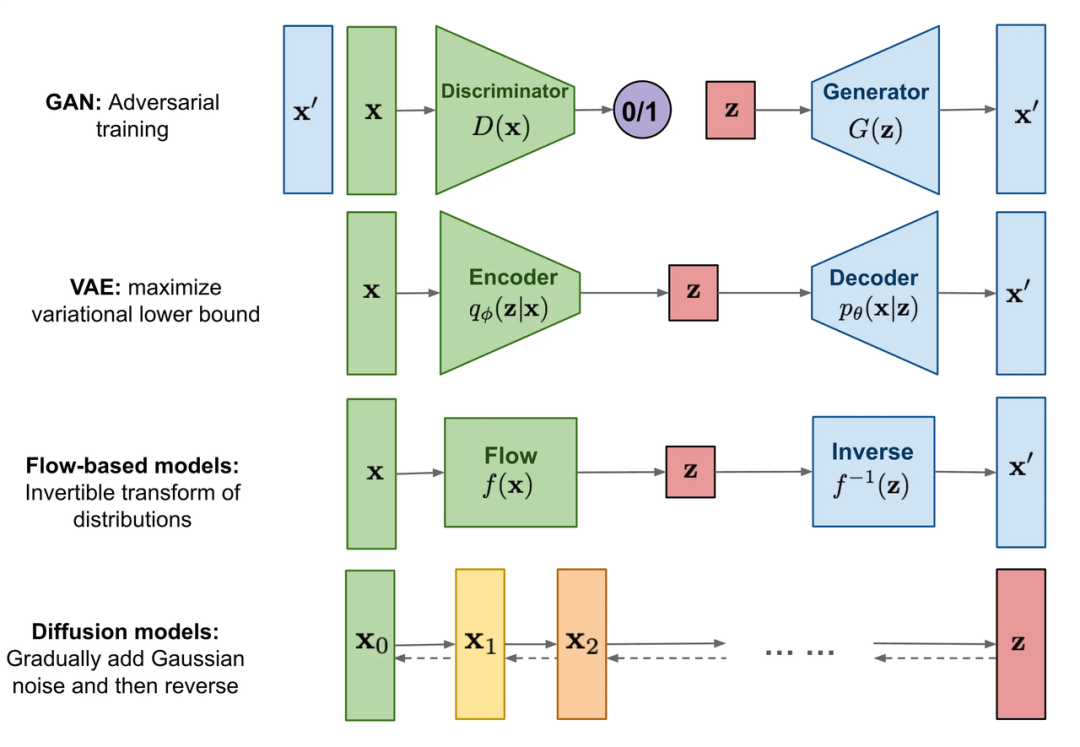
所有类型的生成模型最终都旨在解决相同任务,但它们对密度函数的建模方法都略有不同, 一般来说有以下两类:
对密度函数显式建模 (explicitly modeling),
但以某种方式约束模型,以便计算密度函数,比如标准化流模型(normalizing FLOW model)
但是对密度函数做逼近,比如变分自动编码器 (variational autoencoder, VAE) 和扩散模型 (diffusion model)
对密度函数隐式建模 (implicitly modeling),通过直接生成数据的随机过程。比如生成对抗网络 (generative adversarial network, GAN)
总结
生成式人工智能 (GenAI) 是一种可用于创建新的内容和想法 (包括文字、图像、视频和音乐) 的人工智能。与所有人工智能一样,GenAI 是由深度学习模型基于大量数据进行预训练的超大型模型,通常被称为根基模型 (foundation model, FM)。有了 GenAI,我们能画出更炫酷的图像,写出更优美的文字,谱出更动人的音乐,但第一步需要我们去了解 GenAI 怎么创造新的东西,正如文头 Richard Feynman 所说的“我不会明白我无法创造的东西”。



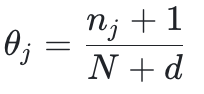
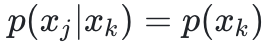







![如何编写AI艺术提示[示例+模板]](https://img-blog.csdnimg.cn/4149588102f74881b4a12e96fec57ae3.png)