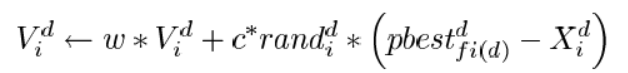1 基本概念

粒子群优化算法（PSO）：它是进化算法的一种，它源于鸟群捕食的行为研究，基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。在PSO中，每个优化问题的潜在解都是搜索空间中的一只鸟，抽象为粒子，每个粒子都有一个由目标函数决定的适应值，以及决定它们飞行的方向和距离。
粒子几点解释：
1、每个寻优问题的解被称为“粒子”，所有粒子都在一个D维空间内进行搜索
2、每个粒子都由一个适应度函数确定适应值以判断目前位置的好坏
3、每一个粒子都有记忆功能，能记住它经过的最佳位置
4、每一个粒子有一个速度以决定其移动的距离和方向

2 算法实现

算法流程
在这里插入图片描述
1、初始化：
初始化粒子群，给每个粒子赋予随机的初始位置和速度
2、计算适应值：
根据适应度函数，计算每个粒子的适应值
3、求个体最佳适应值：
对每个粒子，将其当前位置适应值与其历史最佳位置对应适应值比较，若当前位置适应值更高，则用当前位置更新历史最佳位置
4、求群体最佳适应值：
对每一个粒子，将其当前位置适应值与其全局最佳位置对应适应值比较，如果当前位置的适应值更高，则用当前位置更新全局最佳位置
5、更新粒子位置和速度：
根据公式更新每个粒子的速度与位置
6、判断算法是否结束：
通常算法达到最大迭代次数或者最佳适应度值的增量小于某个给定的阈值时算法停止
速度位置更新公式：
粒子i的第D维速度更新公式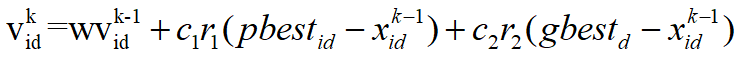：在这里插入图片描述
粒子i的第D维位置更新公式：

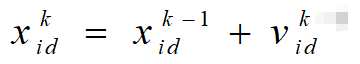
几点说明：

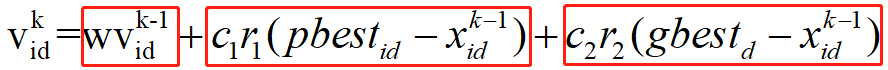
第一部分为粒子先前的速度
第二部分为“认知部分”，表示粒子本身的思考，可理解为粒子i当前位置与自己最好位置之间的距离
第三部分为“社会部分”，表示粒子间的信息共享和合作，可理解为粒子i当前位置与群体最好位置之间的距离。
粒子的速度是三个方向速度的加权矢量和
在这里插入图片描述

3 算法优化举例

y = (Asin(A) cos(2A) - 2 A sin(3 A))×(B sin(B) cos(2 B) - 2 Bsin(3 B))
Matlab代码实现

//粒子群算法Matlab代码实现
clc;clear;close all;
%% 初始化种群
f= @(a,b)(a .* sin(a) .* cos(2 * a) - 2 * a .* sin(3 * a)).*(b .* sin(b) .* cos(2 * b) - 2 * b .* sin(3 * b)); % 函数表达式
figure(1);
[x0_1, x0_2]=meshgrid(0:.2:20);
y0=f(x0_1,x0_2);
mesh(x0_1, x0_2, y0);
hold on;N = 500;                         % 初始种群个数
d = 2;                          % 空间维数
ger = 300;                      % 最大迭代次数     
limit = [0, 20;0,20];                % 设置位置参数限制(矩阵的形式可以多维)
vlimit = [-1.5, 1.5;-1.5, 1.5];               % 设置速度限制
c_1 = 0.8;                        % 惯性权重
c_2 = 0.5;                       % 自我学习因子
c_3 = 0.5;                       % 群体学习因子 for i = 1:dx(:,i) = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, 1);%初始种群的位置
end    
v = rand(N, d);                  % 初始种群的速度
xm = x;                          % 每个个体的历史最佳位置
ym = zeros(1, d);                % 种群的历史最佳位置
fxm = zeros(N, 1);               % 每个个体的历史最佳适应度
fym = -inf;                      % 种群历史最佳适应度plot3(xm(:,1),xm(:,2),f(xm(:,1),xm(:,2)), 'ro');title('初始状态图');
hold on;
figure(2);
mesh(x0_1, x0_2, y0);
hold on;
plot3(xm(:,1),xm(:,2),f(xm(:,1),xm(:,2)), 'ro');
hold on;
%% 粒子群工作
iter = 1;
times = 1; 
record = zeros(ger, 1);          % 记录器
while iter <= gerfx = f(x(:,1),x(:,2)) ; % 个体当前适应度   for i = 1:N      if fxm(i) < fx(i)fxm(i) = fx(i);     % 更新个体历史最佳适应度xm(i,:) = x(i,:);   % 更新个体历史最佳位置end end
if fym < max(fxm)[fym, nmax] = max(fxm);   % 更新群体历史最佳适应度ym = xm(nmax, :);      % 更新群体历史最佳位置endv = v * c_1 + c_2 * rand *(xm - x) + c_3 * rand *(repmat(ym, N, 1) - x);% 速度更新% 边界速度处理for i=1:d for j=1:Nif  v(j,i)>vlimit(i,2)v(j,i)=vlimit(i,2);endif  v(j,i) < vlimit(i,1)v(j,i)=vlimit(i,1);endendend       x = x + v;% 位置更新% 边界位置处理for i=1:d for j=1:Nif  x(j,i)>limit(i,2)x(j,i)=limit(i,2);endif  x(j,i) < limit(i,1)x(j,i)=limit(i,1);endendendrecord(iter) = fym;%最大值记录if times >= 10cla;mesh(x0_1, x0_2, y0);plot3(x(:,1),x(:,2),f(x(:,1),x(:,2)), 'ro');title('状态位置变化');pause(0.5);times=0;enditer = iter+1;times=times+1;
end
figure(3);plot(record);title('收敛过程')
figure(4);
mesh(x0_1, x0_2, y0);
hold on;
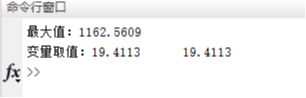
plot3(x(:,1),x(:,2),f(x(:,1),x(:,2)), 'ro');title('最终状态图');disp(['最大值：',num2str(fym)]);
disp(['变量取值：',num2str(ym)]);

在这里插入图片描述

4 算法构成要素分析

1.种群大小N
N过小，陷入局优的可能性很大； N过大，优化能力很好，但计算时间大幅提高，收敛速度慢。
2.权重因子w
w较大，有利于跳出局部极小点，增强粒子的全局搜索能力。w较小，利于粒子的局部搜索能力
3.最大速度
作用在于维护算法的探索能力与开发能力的平衡, Vm较大时，增强了全局搜素能力，但粒子容易飞过最优解，导致局部搜索能力下降。较小时，开发能力增强，但会极大地增加全局搜索的时间，容易陷入局部最优。速度取值一般为优化变量范围的10-20%。
4.学习因子c1、c2
c1=0，“只有社会，没有自我”迅速丧失群体多样性，易陷入局优而无法跳出。c2=0，“只有自我，没有社会”完全没有信息的社会共享，导致算法收敛速度缓慢。

5算法优缺点分析

PSO算法的优点：
算法通用性强，不依赖于问题信息，全局搜索精度高。
群体搜索，并具有记忆功能，保留局部个体和全局种群的最优信息，无需梯度信息。
原理结构简单，设置参数少，容易实现。
协同搜索，同时利用个体局部信息和群体全局信息指导搜索，收敛速度快。
PSO算法的缺点：
算法局部搜索能力较差，搜索精度不够高。
算法不能够绝对保证搜索到全局最优解，容易陷入局部最优解。
算法搜索性能对参数具有一定的依赖性。

6 算法图像分割中应用

粒子群算法优化OTSU图像分割：
1.粒子群的个体初始化
确定种群数量，在OTSU图像分割中一般设定粒子群数量为15，这15个粒子代表15个不同的灰度值（15个不同的阈值），这15个粒子的灰度值只能在0-255内的整数
2.设置每个粒子的初始速度
初始速度就相当于每次改变位置的步长，不能太大也不能太小，更不能超出0-255范围
3.计算每个粒子的最佳位置和全局最佳位置
根据最大类间方差公式，计算每个粒子的最大类间方差，并找到全局最大类间方差确定其位置
4.判断算法是否结束
如果全局最大方差对应的位置不是你最终要的位置就重复1～3步骤，直到找到最佳分割阈值。
PSO算法已在图像分割、图像配准、图像融合、图像识别、图像压缩和图像合成等方面发挥作用
在这里插入图片描述