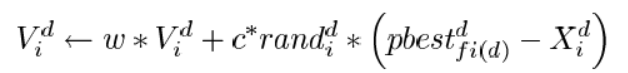粒子群算法的寻优算法记录学习(由于时间关系未添加代码)
粒子群算法(PSO)是计算智能领域,除了蚁群算法,鱼群算法之外的一种群体智能的优化算法。PSO算法源于对鸟类捕食行为的研究,鸟类捕食时,找到食物最简单的策略就是搜寻当前距离食物最近的鸟的周围区域。PSO算法是从这种生物种群行为特征中得到启发并运用于求解优化问题的,算法中的每个粒子都代表问题的一个潜在解,每个粒子对应一个由适应度函数决定的适应度值。粒子群的速度决定了粒子移动的方向和距离,速度随自身及其他粒子的移动经验进行动态调整,从而实现个体在可解空间中的寻优。
PSO算法首先在可行解空间中初始化一些粒子,每个粒子都代表极值优化问题的潜在最优解,用位置,速度和适应度值三项指标表示该粒子的特征,适应度值由适应度函数计算得到,其值的好坏表示粒子的优劣。粒子在空间解运动,通过跟踪个体极值Pbest和群体极值Gbest更新个体的位置。个体极值Pbest是指个体粒子搜索到的适应度值最优位置,群体极值Gbest是指种群中所有粒子搜索得到的适应度最优位置。粒子更新一次位置,就计算一次适应度,并且通过比较新粒子の适应度值和个体极值、群体极值的适应度值更新个体极值Pbest和群体极值Gbest位置。
假设在一个D维的搜索空间中,由n个粒子组成的种群X = (X1,X2,…,Xn),其中第i个粒子表示为一个D维的向量Xi=(Xi1,Xi2,…,Xin)T,代表第i个粒子在D维搜索空间中的位置,亦代表一个问题的潜在解。根据目标函数即可计算出每个粒子位置对应的适应度值。第i个粒子的速度为Vi=(Vi1,Vi2,…,Vin)T,其个体极值为Pi=(Pi1,Pi2,…,Pin)T,种群的群体极值为Pg=(Pg1,Pg2,…,.Pgn)T。
在每次迭代中,粒子通过个体极值和群体极值更新自身的速度和位置,即
上式分别为式1),式2)。
其中,w为惯性权重;
d = 1,2,3,…,D;
i = 1,2,3,…,n;
k为当前迭代的次数;
Vid为粒子的速度;
c1和c2是非负的常数,称为加速度因子;
r1和r2是分布于[0,1]区间的随机数。
为防止粒子的盲目搜索,一般建议将其位置和速度限制在一定的区间[-Xmax,Xmax],[-Xmax,Xmax]。
解题思路及步骤