机器学习吴恩达课程总结(一)

文章目录

- 1. 第一章简介
- - 1.1 机器学习（Machine Learning）
  - 1.2 有监督学习（Supervised Learning）
  - 1.3 无监督学习（Unsupervised Learning）
- 2. 第二章线性回归（Linear Regression）
- - 2.1 假设函数（hypothesis）
  - 2.2 代价函数（cost function）
  - 2.3 简化（Simplified）
  - 2.4 重新加入 ${\theta _0}$ 分析
  - 2.5 梯度下降（Gradient descent）
  - 2.6 梯度下降总结
  - 2.7 线性回归梯度下降
- 3. 第三章线性代数基础
- - 3.1 矩阵和向量（Matrices and vectors）
  - 3.2 矩阵加减与标量(scalar)运算
  - 3.3 矩阵向量乘法
  - 3.4 矩阵乘法
  - 3.5 矩阵乘法特征
  - 3.6 逆和转置
- 4. 第四章多元线性回归
- - 4.1 多元特征
  - 4.2 多元变量梯度下降
  - 4.3 多元变量梯度下降：特征缩放（Feature Scaling）
  - 4.4 多元变量梯度下降：学习率 $\alpha$
  - 4.5 特征和多项式回归
  - 4.6 正规方程（Normal equation）解析解法
  - 4.7 正规方程：不可逆矩阵
- 5. 第五章 Octave基础

1. 第一章简介

1.1 机器学习（Machine Learning）

机器学习：研究能够从经验中自动提升自身性能的计算机算法。

从数学角度：机器学习就是从数据中学习一个函数𝑓 。

机器学习：能过从针对任务T的一些经验E和性能指标P中学习的计算机程序。同时它在任务T上的表现可以通过性能指标P来提高。

1.2 有监督学习（Supervised Learning）

给出“正确答案”。

回归（Regression）：输出连续的值。

分类（Classification）：输出离散的值。

1.3 无监督学习（Unsupervised Learning）

不给出任何标签，找到数据中暗含的结构或信息。

聚类算法（Clustering）：

组织计算集群
社交网络分析
市场分割
天文数据分析

2. 第二章线性回归（Linear Regression）

2.1 假设函数（hypothesis）

h：hypothesis假设函数： ${h_\theta }(x) = {\theta _0} + {\theta _1x}$ ，其中 ${\theta _0},{\theta _1}$ 表示要学习的参数。

2.2 代价函数（cost function）

cost function代价函数

目标：选出 ${\theta _0},{\theta _1}$ 使得在训练集上，给出 $x$ 能够合理准确地预测出 $y$ 的值。

学习目标：
$\mathop {minimize}\limits_{{\theta _0}{\theta _1}} {1 \over {2m}}\sum\limits_{i = 1}^m {{{({h_\theta }({x_i}) - {y_i})}^2}}$

其中 ${x_i},{y_i})$ 表示第 $i$ 个样本； $m$ 表示样本总数。（之所以乘以 $\over 2}$ 是为了方便求导）

令： $J({\theta _0},{\theta _1}) = {1 \over {2m}}\sum\limits_{i = 1}^m {{{({h_\theta }({x_i}) - {y_i})}^2}}$

目标函数简写为： $\mathop {minimize}\limits_{{\theta _0}{\theta _1}} J({\theta _0},{\theta _1})$

$\mathop {minimize}$ ：表示使得后面式子最小时， ${\theta _0},{\theta _1}$ 的取值。

$J({\theta _0},{\theta _1})$ 称为：代价函数(cost function)，优化目标(optimization objective)。

小提示： 损失函数“（Loss Function ）是定义在单个样本上的，算的是一个样本的误差，而代价函数（Cost Function ）是定义在整个训练集上的，是所有样本误差的平均，也就是损失函数的平均。

2.3 简化（Simplified）

${h_\theta }(x) = {\theta _1}x$ 假设 ${\theta _0}=0$

$J({\theta _0},{\theta _1}) \to J({\theta _1})$

2.4 重新加入 ${\theta _0}$ 分析

假设函数： ${h_\theta }(x) = {\theta _0} + {\theta _1}x$

可学习参数： ${\theta _0},{\theta _1}$

损失函数： $J({\theta _0},{\theta _1}) = {1 \over {2m}}\sum\limits_{i = 1}^m {{{({h_\theta }({x_i}) - {y_i})}^2}}$

目标： $\mathop {minimize}\limits_{{\theta _0}{\theta _1}} J({\theta _0},{\theta _1})$

2.5 梯度下降（Gradient descent）

问题描述：

有一些函数如： $J({\theta _0},{\theta _1})$ ，想要 $\mathop {minimize}\limits_{{\theta _0}{\theta _1}} J({\theta _0},{\theta _1})$ 。

解决步骤：

设置 ${\theta _0},{\theta _1}$ 初值通常为 $0$
改变 ${\theta _0},{\theta _1}$ （通常以较小值改变）减少 $J({\theta _0},{\theta _1})$ 直到我们希望的最小值（可以找到一个局部最小值）

梯度下降算法：

repeat until convergence{ ${\theta _j}: = {\theta _j} - \alpha {\partial \over {\partial {\theta _j}}}J({\theta _0},{\theta _1})$ (for j=0 and j=1)}

$\alpha$ :学习率（learning rate）

注意：同时更新参数 ${\theta _0},{\theta _1}$

2.6 梯度下降总结

${\theta _j}: = {\theta _j} - \alpha {\partial \over {\partial {\theta _j}}}J({\theta _0},{\theta _1})$

$\alpha$ ：过小，收敛慢；过大，可能发散，不收敛。

梯度下降可以收敛到局部最小值，即使学习率 $\alpha$ 固定。

当我们接近局部最小值，梯度下降将要自动得到一个较小的步长。所以，不需要随时间减少学习率 $\alpha$ 。

2.7 线性回归梯度下降

最小化线性回归中的平方损失函数。

${\partial \over {\partial {\theta _j}}}J({\theta _0},{\theta _1}) = {\partial \over {\partial {\theta _j}}}{1 \over {2m}}\sum\limits_{i = 1}^m {{{({h_\theta }({x_i}) - {y_i})}^2}}= {\partial \over {\partial {\theta _j}}}{1 \over {2m}}\sum\limits_{i = 1}^m {{{({\theta _0} + {\theta _1}{x_i} - {y_i})}^2}}$

${{\theta _0}}$ ： $j = 0$ ， ${\partial \over {\partial {\theta _0}}}J({\theta _0},{\theta _1}) = {1 \over m}\sum\limits_{i = 1}^m {{{({h_\theta }({x_i}) - {y_i})}^{}}}$

${{\theta _1}}$ ： $j = 1$ ， ${\partial \over {\partial {\theta _1}}}J({\theta _0},{\theta _1}) = {1 \over m}\sum\limits_{i = 1}^m {{{({h_\theta }({x_i}) - {y_i})}^{}}} {x_i}$

同时更新：

${\theta _0}: = {\theta _0} - \alpha {1 \over m}\sum\limits_{i = 1}^m {{{({h_\theta }({x_i}) - {y_i})}^{}}}$

${\theta _1}: = {\theta _1} - \alpha {1 \over m}\sum\limits_{i = 1}^m {{{({h_\theta }({x_i}) - {y_i})}^{}}} {x_i}$

小提示：凸函数（convex function）：只要一个全局最优

批量梯度下降：每次梯度下降使用所有的训练样本（虽然名字有点歧义）。

3. 第三章线性代数基础

3.1 矩阵和向量（Matrices and vectors）

矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合。

矩阵维数：行数*列数

$A$ ：矩阵， ${A_{ij}}$ ：表示第 $i$ 行第 $j$ 列的元素。

向量： $n * 1$ 的矩阵

$y$ ：向量，n-dimension 向量

3.2 矩阵加减与标量(scalar)运算

两个行列相等的矩阵才可以相加减：对应元素相加减

标量同一个矩阵相加减乘除：标量与每个元素分别运算，矩阵维数不变

3.3 矩阵向量乘法

${A_{m \times n}} \times {x_{n \times 1}} = {y_{m \times 1}}$

${y_{i}}$ 通过 $A$ 的第 $i$ 行与向量 $x$ 对应元素相乘再相加得到。

3.4 矩阵乘法

${A_{m \times n}} \times {B_{n \times o}} = {C_{m \times o}}$

矩阵 $C$ 的第 $i$ 列是通过矩阵 $A$ 和矩阵 $B$ 的第 $i$ 列相乘得到的。

3.5 矩阵乘法特征

$A B = B A$
$\times B \times C = (A \times B) \times C = A \times (B \times C)$
单位矩阵（ ${I_{n \times n}}$ ）满足 ${I_{ii}}=1$ ， $I$ 可以根据需要取不同的维数，如 ${A_{m \times n}} \times {I_{n \times n}} = {I_{m \times m}} \times {A_{m \times n}} = A$

3.6 逆和转置

矩阵的逆：方阵才有逆，满足 ${A_{m \times m}}$ $A{A^{ - 1}} = {A^{ - 1}}A = I$

没有逆的矩阵：奇异矩阵（singular），退化矩阵（degenerate）

矩阵的转置：

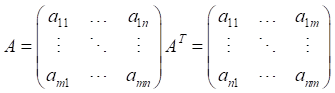
4. 第四章多元线性回归

4.1 多元特征

多元特征：特征数大于2

$n$ 表示特征数量； ${x^{(i)}}$ 表示第 $i$ 个训练样本的所有输入特征； $x_j^{(i)}$ 表示第 $i$ 个训练样本的第 $j$ 个输入特征。

假设函数： ${h_\theta }(x) = {\theta _0} + {\theta _1}{x_1} + {\theta _2}{x_2} + ... + {\theta _n}{x_n}$

令 $\in {R^{n + 1}}$ ， $\theta \in {R^{n + 1}}$ ， ${X_0} = 1$ 则化简公式为： ${h_\theta }(x) = {\theta _0}{x_0} + {\theta _1}{x_1} + {\theta _2}{x_2} + ... + {\theta _n}{x_n} = {\theta ^T}x$

4.2 多元变量梯度下降

假设函数： ${h_\theta }(x) = {\theta _0}{x_0} + {\theta _1}{x_1} + {\theta _2}{x_2} + ... + {\theta _n}{x_n} = {\theta ^T}x$

可学习参数： ${\theta _0},{\theta _1},...{\theta _n}$ ，其中 $\theta \in {R^{n + 1}}$

损失函数： $J({\theta _0},{\theta _1},...{\theta _n}) = {1 \over {2m}}\sum\limits_{i = 1}^m {{{({h_\theta }({x_i}) - {y_i})}^2}} =J({\theta })$

参数更新： ${\theta _j}: = {\theta _j} - \alpha {\partial \over {\partial {\theta _j}}}J({\theta})其中(j=0,1,...,n)$

当 $n > = 1$ 时， ${\theta _j}: = {\theta _j} - \alpha {1 \over m}\sum\limits_{i = 1}^m {{{({h_\theta }({x^{(i)}}) - {y^{(i)}})}^{}}} x_j^{(i)}$
当 $n = = 1$ 时， ${\theta _0}: = {\theta _0} - \alpha {1 \over m}\sum\limits_{i = 1}^m {{{({h_\theta }({x^{(i)}}) - {y^{(i)}})}^{}}}$

4.3 多元变量梯度下降：特征缩放（Feature Scaling）

思想：确保所有特征数值在相似地范围。这样可以走一条相对简单的路径到最优解，要求特征值组之间取值范围相差不大，默认 $\le {x_i} \le 1$ 。

做法：均值归一化（Mean normalization）。使用 ${x_i} - {\mu _i}$ 代替 ${x_i}$ 确保 $0$ 均值。

${x_i} \leftarrow {{{x_i} - {\mu _i}} \over {{S_i}}}$ ，其中 ${{\mu _i}}$ 表示该特征均值， ${{S_i}}$ 表示取值范围（最大值减去最小值）

4.4 多元变量梯度下降：学习率 $\alpha$

如何判断梯度下降算法是否正确工作？

若正常工作在每次迭代后， $J(\theta )$ 都应该减少，可以绘制 $J(\theta )$ 随迭代次数变化的函数判断。

自动收敛测试（automatic convergence test）：每次迭代后 $J(\theta )$ 下降的值超过 $\varepsilon (小正数如：{10^{ - 3}})$ 。

如果未正常工作可以使用更小的 $\alpha$ 。

对于足够小的 $\alpha$ ， $J(\theta )$ 应该每次迭代均会下降，但是如果 $\alpha$ 太小，则会导致收敛速度太慢。

如何选择 $\alpha$ ？

$. . ., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1 . . .$ ，采用3倍策略（经验）

4.5 特征和多项式回归

例： ${\theta _0} + {\theta _1}x + {\theta _2}{x^2} + {\theta _3}{x^3}$ 映射到多元线性回归 ${h_\theta }(x) = {\theta _0} + {\theta _1}{x_1} + {\theta _2}{x_2} + {\theta _3}{x_3}$ 可以用少量特征学习更加复杂的关系。

${x_1} = (size),{x_2} = {(size)^2},{x_3} = {(size)^3}$ ，这时特征缩放更为重要。

4.6 正规方程（Normal equation）解析解法

自觉：对于一维的情况，好像在 $J(\theta )$ 导数为0时可以取得最优解。
$J({\theta _0},{\theta _1},...,{\theta _n}) = {1 \over {2m}}\sum\limits_{i = 1}^m {{{({h_\theta }({x^{(i)}}) - {y^{(i)}})}^2}} ，\theta \in {R^{n + 1}}$