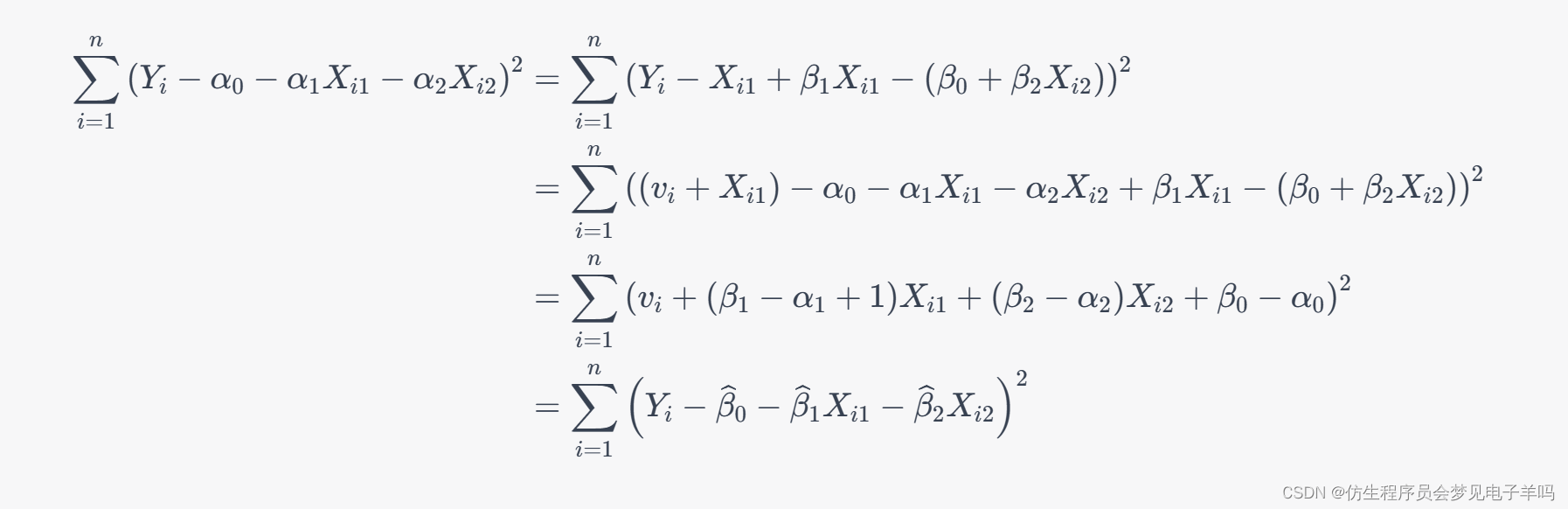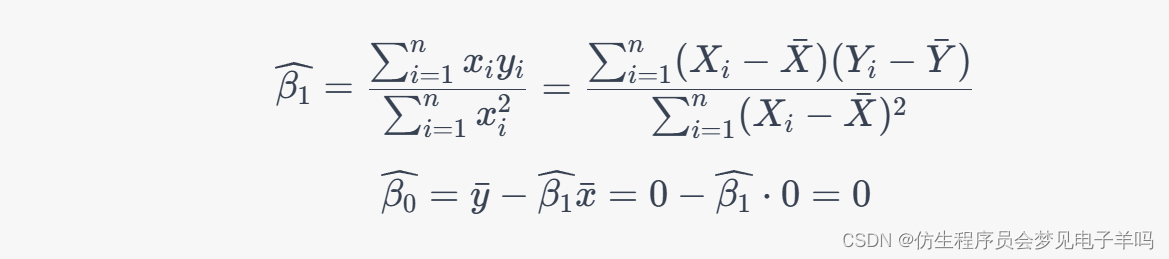https://antkillerfarm.github.io/
前言
神经网络本质上不是什么新东西。十年前,我还在上学的时候,就接触过皮毛。然而那时这玩意更多的还是学术界的屠龙之术,工业界几乎没有涉及。
及至近日重新拾起,方才发现,这十年正是神经网络蓬勃发展,逐渐进入应用阶段的十年。各种概念层出不穷,远非昔日模样。
Deep Learning虽然在学术界的大牛看来,属于旧概念的炒作。然而由于神经网络本身的非线性和连接的复杂性,其中的概念的确比一般的浅层算法复杂的多,从这个角度来说,称其为Deep,也算有些道理。
这里最主要的参考文献包括:
《机器学习》,周志华著。
《Deep Learning Tutorial》,李宏毅著(台湾大学电机工程学助理教授)。
http://www.useit.com.cn/thread-13132-1-1.html
《Deep Learning》,Ian Goodfellow、Yoshua Bengio、Aaron Courville著。
原版:
http://www.deeplearningbook.org/
中文版:
https://github.com/exacity/deeplearningbook-chinese
注:这本书基于markdown文件,使用tex编译而成,可作为编写大型书的代码参考项目。
安装方法:
sudo apt install texlive-xetex texlive-lang-chinese texlive-science xindy
make
其他参考文献将在各相关部分列出。
Deep Learning圈子的主要人物:
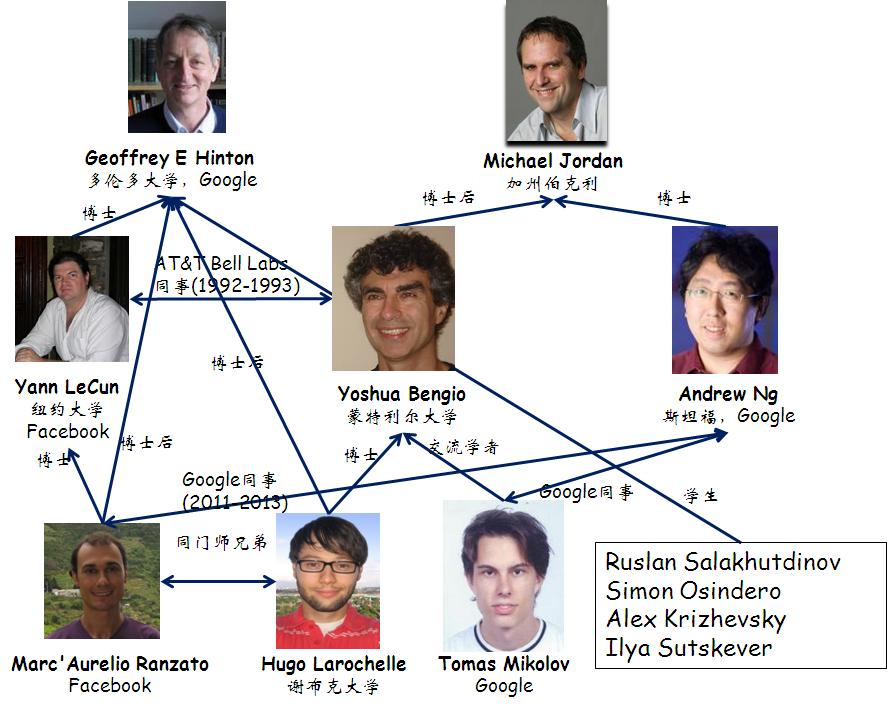
注:Yann LeCun,1960年生,法国科学家。Pierre and Marie Curie University博士。Geoffrey Hinton是他博士后时代的导师。CNN的发明人。纽约大学教授,Facebook AI研究所主任。由于他的姓名发音非常东方化,因此被网友起了很多中文名如燕乐存、杨乐康等。2017.3,Yann访华期间正式公布中文名:杨立昆。
Léon Bottou,法国科学家,随机梯度下降算法的发明人。
Yoshua Bengio,1964年生,法国出生的加拿大科学家。深度学习的另一个宗师。
这三个法国佬,都是好基友。只不过Yann LeCun和Yoshua Bengio研究神经网络,而Léon Bottou研究SVM,学术上分属不同派系。
Geoffrey Everest Hinton,1947年生,英国出生的加拿大科学家,爱丁堡大学博士,多伦多大学教授。连接主义的代表人物,多层神经网络的宗师。英国皇家学会会员。
一般将Geoffrey Hinton、Yann LeCun和Yoshua Bengio并称为深度学习的三大宗师。
MP神经元模型
MP神经元模型是1943年,由Warren McCulloch和Walter Pitts提出的。
注:Warren Sturgis McCulloch,1898~1969,美国神经生理学和控制论科学家。哥伦比亚大学博士,先后执教于MIT、Yale、芝加哥大学。
Walter Harry Pitts, Jr.,1923~1969,美国计算神经学科学家。
这个人的经历,实在是非典型。家里贫穷,大约是读不起大学,15岁的时候,到芝加哥大学旁听Bertrand Russell的讲座。Russell很看重这个年轻人,但由于他只是访问学者,于是在回国之前,将Pitts介绍给Rudolf Carnap,后者为Pitts安排了一份在学校打杂的工作。这一打杂就是五六年时间,最后凭借论文,获得芝加哥大学的准学士学位(因为他始终都不是正式学籍的学生),这也是他一生唯一的学位。
但是如果看看Pitts的合作者的阵容,就知道Pitts水平之高了。他们是:Warren McCulloch、Jerome Lettvin、Norbert Wiener。
MP神经元模型如下图所示:
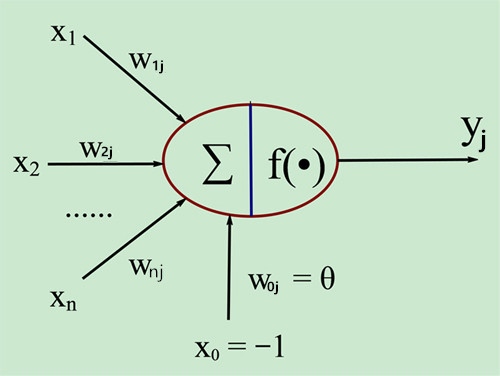
即:
y j = f ( ∑ i = 1 n w i j x i − θ j ) y_j=f\left(\sum _{i=1}^nw_{ij}x_i-\theta_j\right) yj=f(i=1∑nwijxi−θj)
f被称为称为激活函数(Activation Function)或转移函数(Transfer Function),用以提供非线性表达能力。f的参数其实就是《机器学习(一)》中提到的逻辑回归。
生物神经元和MP神经元模型的对应关系如下表:
| 生物神经元 | MP神经元模型 |
|---|---|
| 神经元 | j j j |
| 输入信号 | x i x_i xi |
| 权值 | w i j w_{ij} wij |
| 输出信号 | y j y_j yj |
| 总和 | ∑ \sum ∑ |
| 膜电位 | ∑ i = 1 n w i j x i \sum _{i=1}^nw_{ij}x_i i=1∑nwijxi |
| 阈值 | θ j \theta_j θj |
从上图亦可看出,如果将阈值看作输入为-1.0的哑节点的连接权重,则权重和阈值可统一为权重。神经网络训练的过程,实际上就是根据样本调整权重和阈值的过程。
参考:
http://blog.csdn.net/u013007900/article/details/50066315
单层感知器 vs. 多层感知器
神经网络的层数越多,其表达力越丰富,如下表所示:
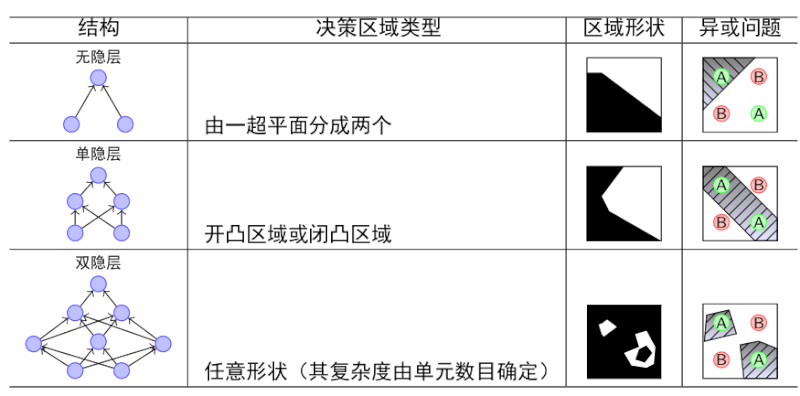
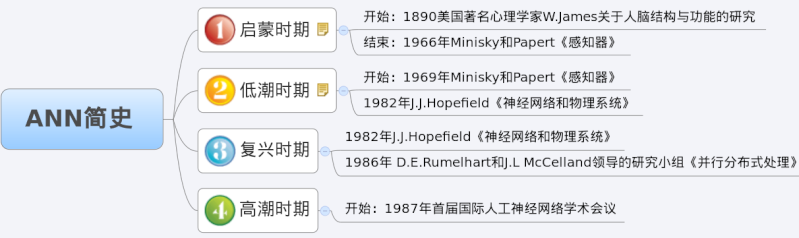
ANN简史
BP算法
误差逆传播(error BackPropagation)算法最早由Paul J. Werbos于1974年提出,然而此时正值ANN的低谷,未得到人们的重视。因此到了1986年时,由David Everett Rumelhart重新发明了该算法。
注:Paul J. Werbos,1947年生,哈佛大学博士。
David Everett Rumelhart,1942~2011,美国心理学家。斯坦福大学博士,先后执教于UCSD和斯坦福。美国科学院院士。
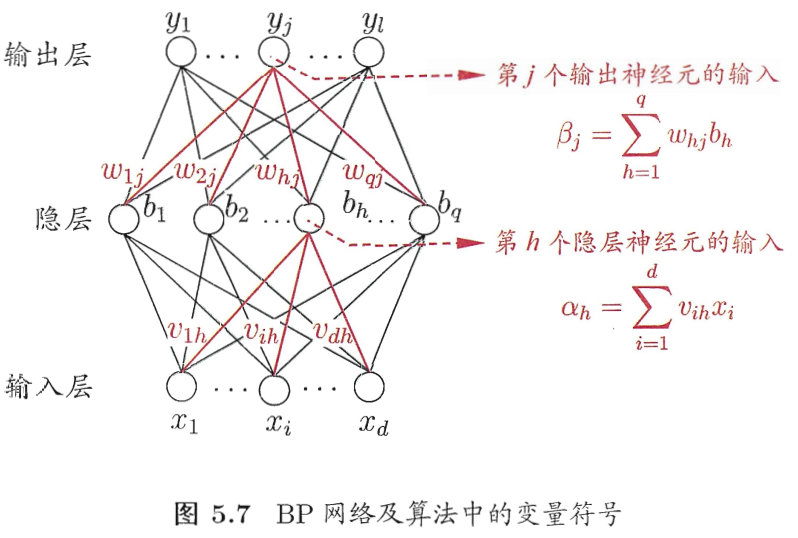
BP算法的核心思路:
1.利用前向传导公式,计算第n层输出值。
2.计算输出值和实际值的残差。
3.将残差梯度传递回第 n − 1 , n − 2 , … , 2 n-1,n-2,\dots,2 n−1,n−2,…,2层,并修正各层参数。(即所谓的误差逆传播)
BP算法的推导过程教材已经写的很好了,这里只对要点做一个摘录。
链式法则
Chain Rules本来是微积分中,用于求一个复合函数导数的常用法则。这里用来进行残差梯度的逆传播。
由《机器学习(一)》的公式3可得:
Δ w h j = − η ∂ E k ∂ w h j \Delta w_{hj}=-\eta\frac{\partial E_k}{\partial w_{hj}} Δwhj=−η∂whj∂Ek
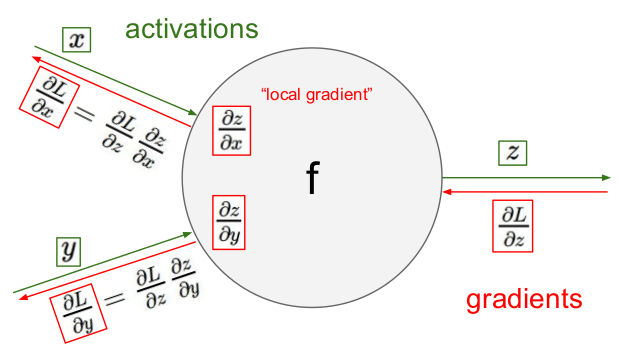
w h j w_{hj} whj先影响 β j \beta_j βj,再影响 y ^ j k \hat y_j^k y^jk,然后影响误差 E k E_k Ek,因此有:
∂ E k ∂ w h j = ∂ E k ∂ y ^ j k ⋅ ∂ y ^ j k ∂ β j ⋅ ∂ β j ∂ w h j (1) \frac{\partial E_k}{\partial w_{hj}}=\frac{\partial E_k}{\partial \hat y_j^k}\cdot \frac{\partial \hat y_j^k}{\partial \beta_j}\cdot \frac{\partial \beta_j}{\partial w_{hj}}\tag{1} ∂whj∂Ek=∂y^jk∂Ek⋅∂βj∂y^jk⋅∂whj∂βj(1)
随机初始化
神经网络的参数的随机初始化的目的是使对称失效。否则的话,所有对称结点的权重都一致,也就无法区分并学习了。
BP算法的缺点
虽然传统的BP算法,理论上可以支持任意深度的神经网络。然而实际使用中,却很少能支持3层以上的神经网络。
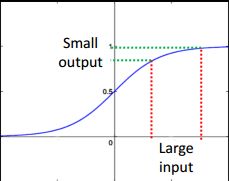
如上图所示,sigmoid函数不是线性的,一个小的输出值的改变,对应了比较大的输入值改变。换句话说,就是输出值的梯度较大,而输入值的梯度较小。而梯度在基于梯度下降的优化问题中,是至关重要的。
随着层数的增多,反向传递的残差梯度会越来越小,这样的现象,被称作梯度消失(Vanishing Gradient)。它导致的结果是,虽然靠近输出端的神经网络已经训练好了,但输入端的神经网络仍处于随机状态。也就是说,靠近输入端的神经网络,有和没有都是一样的效果,完全体现不了深度神经网络的优越性。
和梯度消失相反的概念是梯度爆炸(Vanishing Explode),也就是神经网络无法收敛。
神经元激活函数
tanh函数
除了阶跃函数和Sigmoid函数之外,常用的神经元激活函数,还有双曲正切函数(tanh函数):
f ( z ) = tanh ( x ) = sinh ( x ) cosh ( x ) = e x − e − x e x + e − x f(z)=\tanh(x)=\frac{\sinh(x)}{\cosh(x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}} f(z)=tanh(x)=cosh(x)sinh(x)=ex+e−xex−e−x
其导数为:
f ′ ( z ) = 1 − ( f ( z ) ) 2 f'(z)=1-(f(z))^2 f′(z)=1−(f(z))2
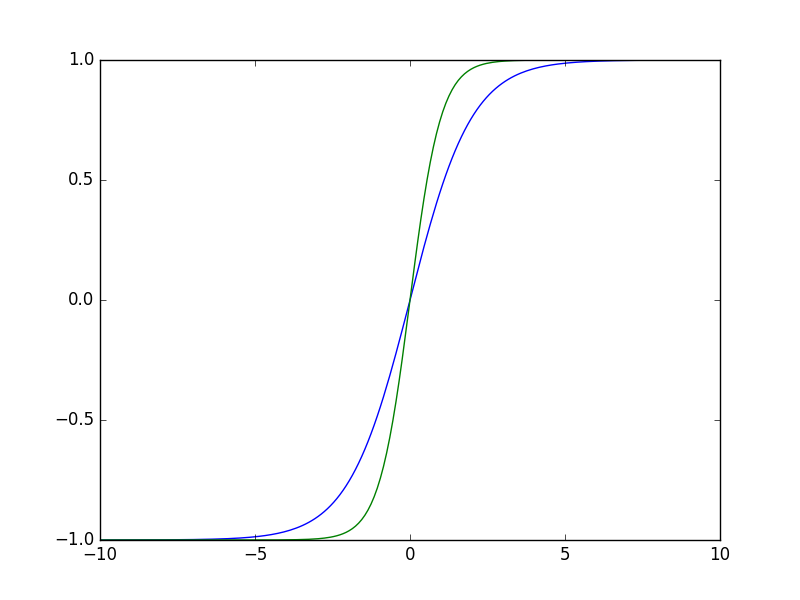
上图是sigmoid函数(蓝)和tanh函数(绿)的曲线图。
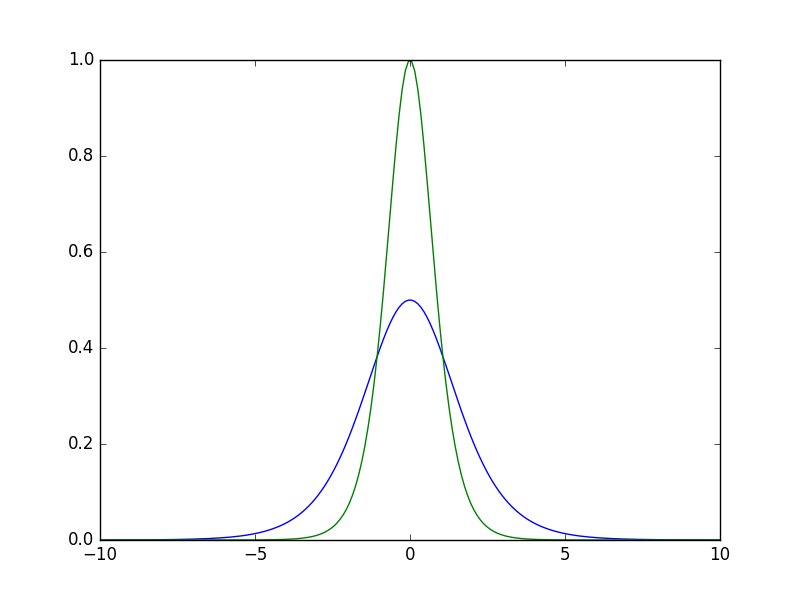
上图是sigmoid函数(蓝)和tanh函数(绿)的梯度曲线图。从中可以看出tanh函数的梯度比sigmoid函数大,因此有利于残差梯度的反向传递,这是tanh函数优于sigmoid函数的地方。但是总的来说,由于两者曲线类似,因此tanh函数仍被归类于sigmoid函数族中。
下图是一些sigmoid函数族的曲线图:
有关sigmoid函数和tanh函数的权威论述,参见Yann LeCun的论文:
http://yann.lecun.com/exdb/publis/pdf/lecun-98b.pdf
稀疏性
从数学上来看,非线性的Sigmoid函数对中央区的信号增益较大,对两侧区的信号增益小,在信号的特征空间映射上,有很好的效果。
从神经科学上来看,中央区酷似神经元的兴奋态,两侧区酷似神经元的抑制态,因而在神经网络学习方面,可以将重点特征推向中央区,将非重点特征推向两侧区。
无论是哪种解释,看起来都比早期的线性激活函数 y = x y=x y=x,阶跃激活函数高明了不少。
2001年,Attwell等人基于大脑能量消耗的观察学习上,推测神经元编码工作方式具有稀疏性和分布性。
2003年,Lennie等人估测大脑同时被激活的神经元只有1~4%,进一步表明神经元工作的稀疏性。
从信号方面来看,即神经元同时只对输入信号的少部分选择性响应,大量信号被刻意的屏蔽了,这样可以提高学习的精度,更好更快地提取稀疏特征。
从这个角度来看,在经验规则的初始化W之后,传统的Sigmoid系函数同时近乎有一半的神经元被激活,这不符合神经科学的研究,而且会给深度网络训练带来巨大问题。
参考:
http://www.cnblogs.com/neopenx/p/4453161.html
https://en.wikipedia.org/wiki/Activation_function
ReLU
ReLU(Rectified Linear Units)激活函数的定义如下:
f ( x ) = max ( 0 , x ) f(x) = \max(0, x) f(x)=max(0,x)
其函数曲线如下图中的蓝线所示:
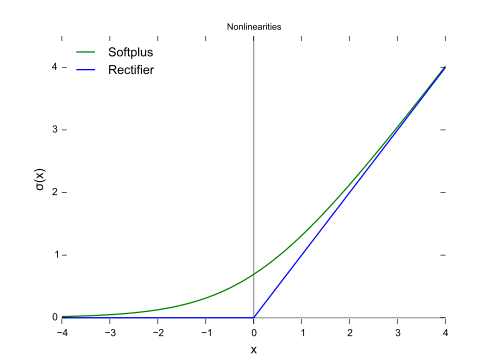
从上图可以看出,ReLU相对于Sigmoid,在解决了梯度消失问题的同时,也增加了神经网络的稀疏性,因此ReLU的收敛速度远高于Sigmod,并成为目前最常用的激活函数。
由于ReLU的曲线不是连续可导的,因此有的时候,会用SoftPlus函数(上图中的绿线)替代。其定义为:
f ( x ) = ln ( 1 + e x ) f(x) = \ln(1 + e^x) f(x)=ln(1+ex)
除此之外,ReLU函数族还包括Leaky ReLU、PReLU、RReLU、ELU等。
Dropout
Dropout是神经网络中解决过拟合问题的一种常见方法。
它的具体做法是:
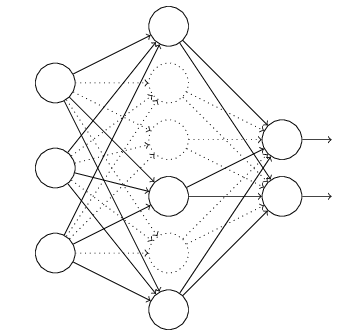
1.每次训练时,随机隐藏部分隐层神经元。
2.根据样本值,修改未隐藏的神经元的参数。隐藏的神经元的参数保持不变。
3.下次训练时,重新随机选择需要隐藏的神经元。
由于神经网络的非线性,Dropout的理论证明尚属空白,这里只有一些直观解释。
1.dropout掉不同的隐藏神经元就类似在训练不同的网络,整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合,一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。这实际上就是bagging的思想。
2.因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这会迫使网络去学习更加鲁棒的特征。换句话说,假如我们的神经网络是在做出某种预测,它不应该对一些特定的线索片段太过敏感,即使丢失特定的线索,它也应该可以从众多其它线索中学习一些共同的模式(鲁棒性)。