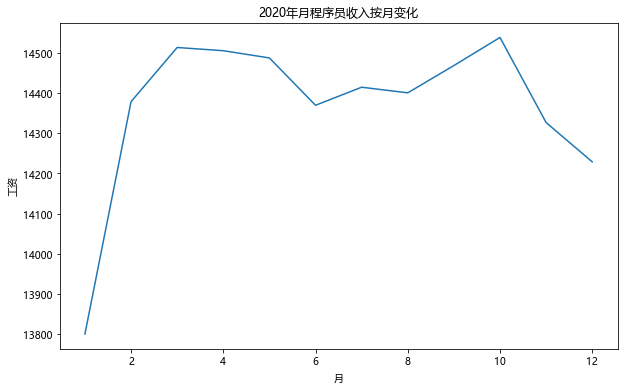
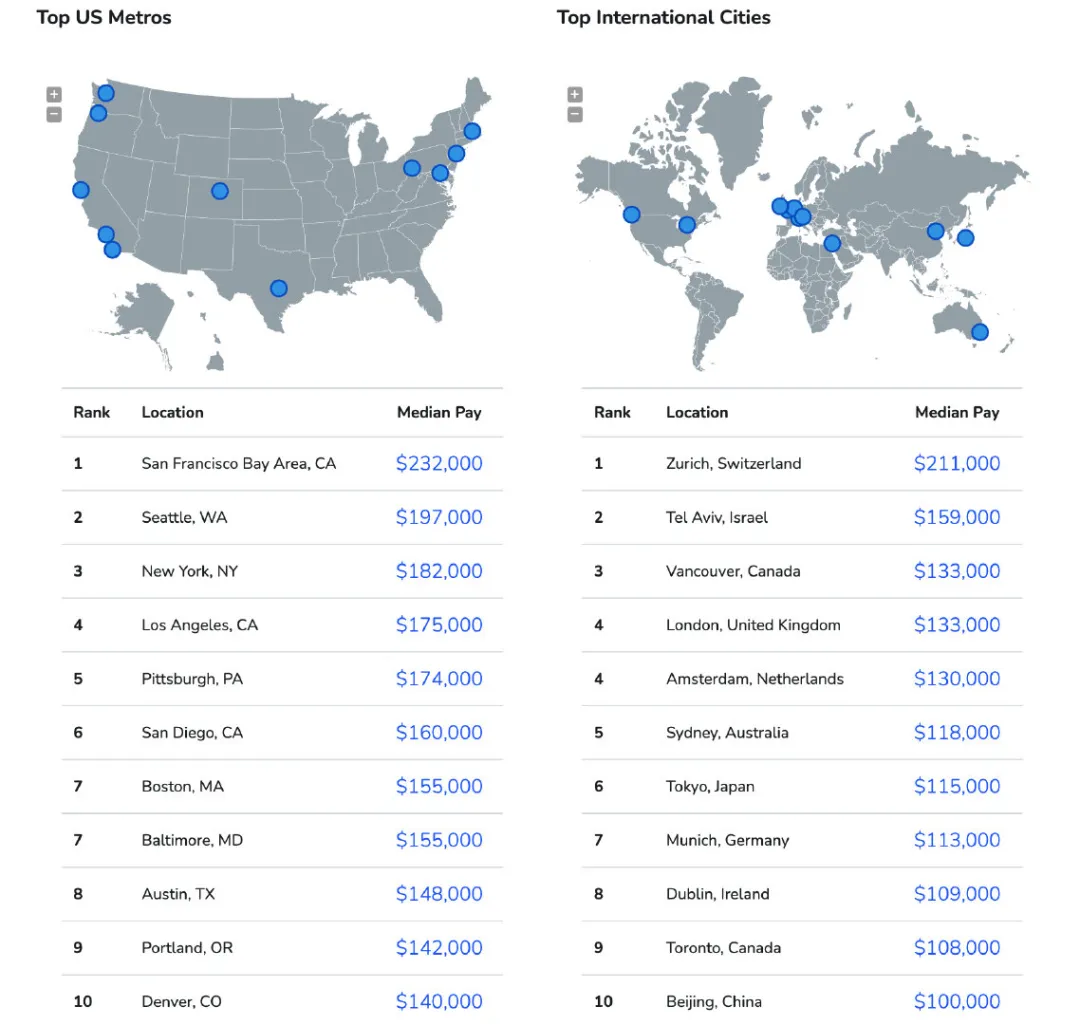
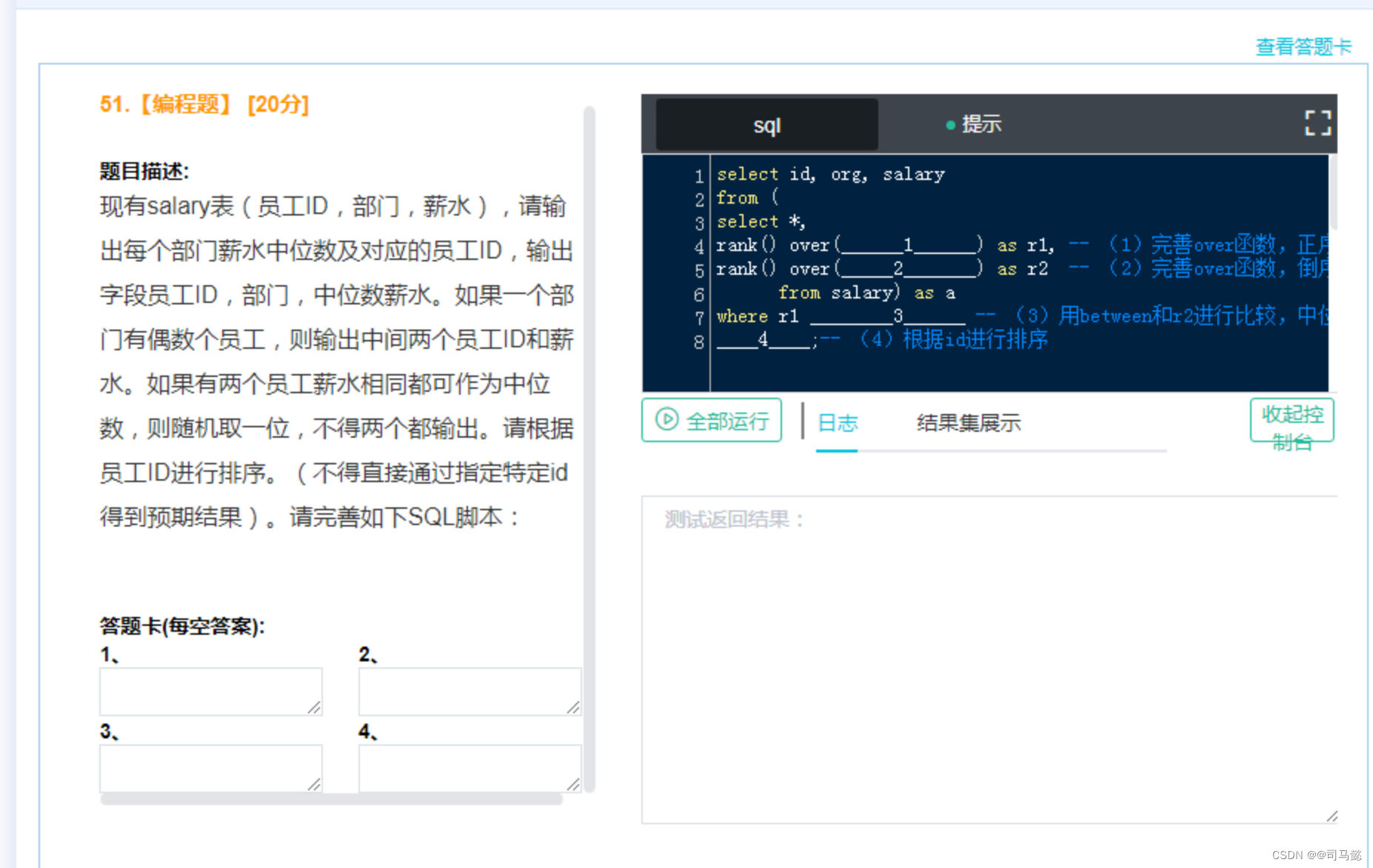
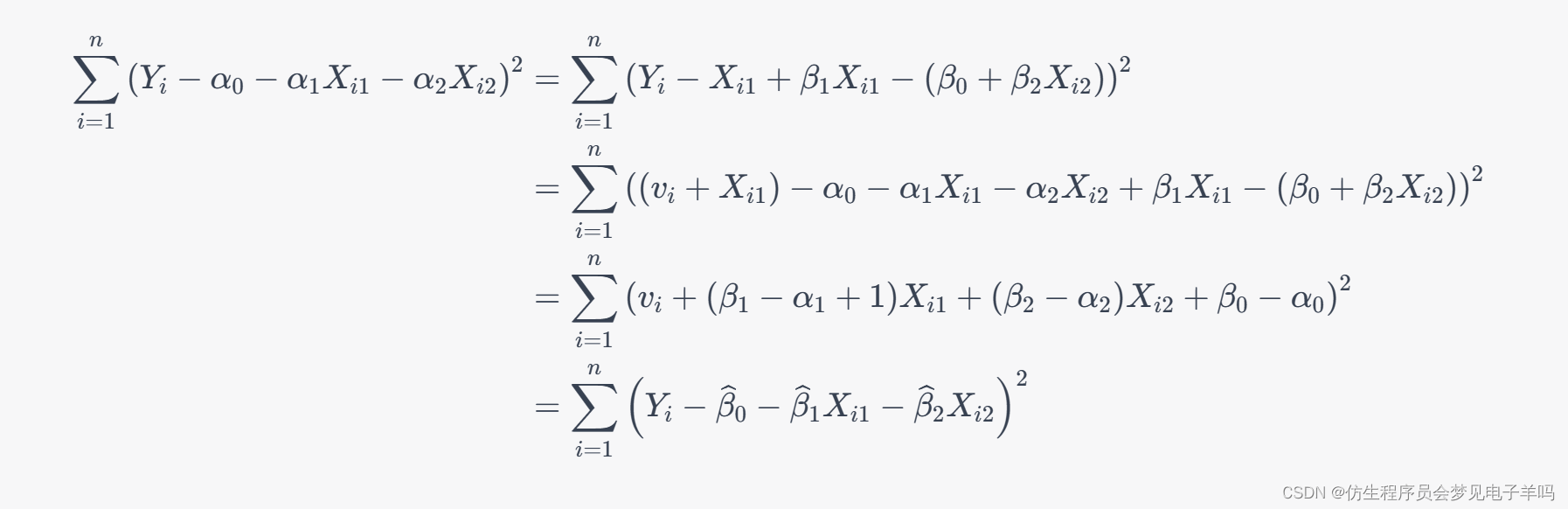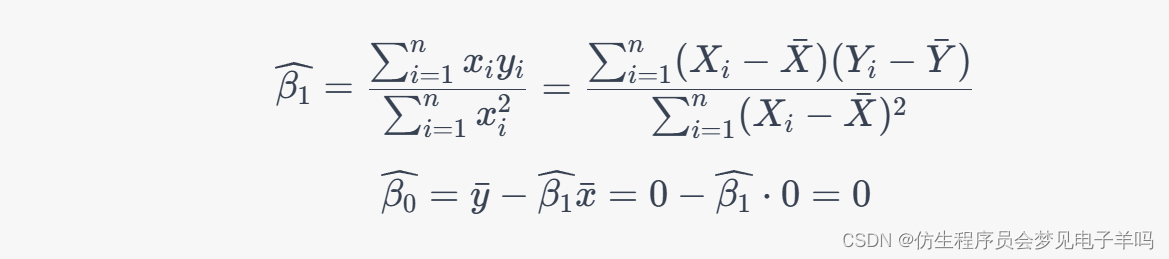神经元多输入

  上一篇博客介绍了二分类的逻辑回归模型。如果我们想要多分类的逻辑回归模型，我们该怎么做呢？

  很显然，我们在只有一个神经元的时候可以做二分类的问题。如果我们想要多分类的话，直接加神经元的个数就好了，使用多个神经元就能得到多输出的回归模型。如下图所示，我们又多加了一个神经元，之后就可以得到两个输出，那么就可以去做三分类的逻辑回归。

  
  这里多加一个神经元就相当于把 $W$ 从向量扩展为矩阵，输出的 $W\ast x$ 从一个值变成了一个向量。
  
  下面举一个简单的例子，比如输入的 $X$ = [3, 1, 2]，$W$ = [ [0.4, 0.6, 0.5], [0.3, 0.2, 0.1] ]，那么我们可以计算出 $Y0$ 和 $Y1$。
  

  
  我们将有多个输出的神经元叫做多输出神经元，那么我们有了多输出神经元之后，那么我们怎么对之前的二分类逻辑斯蒂回归模型进行扩展，将其扩展为多分类逻辑斯蒂回归模型。其实二分类在现实生活中应用比较少，所以遇到的一般都还是多分类问题。所以多分类问题比二分类问题具有更广泛的适用性。

  我们先回顾之前的二分类问题，二分类问题只有一个神经元，神经元只有一个输出，它的输出经过一个 sigmoid 函数然后得到相应结果，这个结果我们可以认为它是对于 $Y=0$ 这个类的一个概率估计，那么相应的我们也能得到 $Y=1$ 这个类的概率估计。
  

  
  那么我们还可以从另外一个角度去看它。我们可以看出这两个 $P$ 的值分子一个是 1，一个是 $e^{(}-w^{T}x)$，分母是相同的，那么我们可以把分母看成是数据归一化（把数据归到同一个量纲上）的过程。
  
  比如一个神经元的输出为 $e^{(}-w^{T}x)$ ，那么和另一个 1 做归一化。我们就得到了和上图式子同样的效果。

  
  因此，我们想要去做扩展，就可以直接将 $W\ast x$ 变成多输出就可以了。
  

  
  仿照二分类概率的公式，可以得到多分类的公式为：
  

  
  这样我们就将一个二分类的逻辑回归模型变成了一个多分类的逻辑回归模型。但是在实际处理的时候，我们会把下图中的 1 和上面的形式相统一，写成 $E^{(}-w^{0}x)$，然后我们使得该值恒等于 1，这样也能达到效果。
  

  
  下面我们仍然举一个简单的例子帮助理解。比如我们现在 $Y$ 的输出为 [2.8，1.3]，激活函数为 $y=e^{(}-x)$。

  
  所以我们就可以得出我们要归一化的分母为 $1+0.06+0.27=1.33$，然后就得到了三个概率：

  
  这样的多分类回归模型和之前介绍的二分类回归模型它们可以被认为是神经网络。
  
  下面我们要介绍的是如何去调整神经网络使得神经网络能够学到数据中的规律，那么首先我们得定义一个目标函数，它是衡量一个模型对数据的拟合程度。目标函数通常也叫做损失函数，还是举一个简单的例子，比如我们的数据样本 $X1$ 是一个向量 [10, 3, 9, 20, …, 4]，这些样本的类别值都是 1，这里我们可以认为是一个二分类问题，它有两个类别值，一个是 1，一个是 0。那么我们将样本 $X$ 放到我们训练的一个模型 Model 中去，得到的分类准确度为 0.8，那么我们相应的损失函数 Loss 的值就应该用这些样本的真值减去样本的预测值得到 0.2。
  

  下面再举出一个多分类问题的例子。比如下面的例子中有 5 类。数据样本 $X1$ 是一个向量 [10, 3, 9, 20, …, 4]，这些样本的类别值都是 3。那么 $y$ 的预测值为拥有 5 个元素的向量，假设得到的 $y$ = [0.1，0.2，0.25，0.4，0.05]，那么最后的 Loss 函数的值为 $y$ 的真值减去 $y$ 的预测值。

  
  这里需要注意一点， Loss 函数需要加上 abs（绝对值） 函数，因为我们最后求得的是距离，距离为正数，所以需要加上一个绝对值函数。
  
  我们定义一个损失函数的形式一般有两种，一种是平方差损失：

  然后另外一种是交叉熵损失，其实这一种是更适合解决多分类问题。因为 $ln$ 函数正好是一个熵函数，熵函数正是衡量两个分布之间的差距的。

  总结一下，其实对于神经网络的训练就是要调整参数使模型在训练集上的损失函数最小。损失函数最小意味着模型预测的结果和真实值之间越接近，即预测结果更准确。