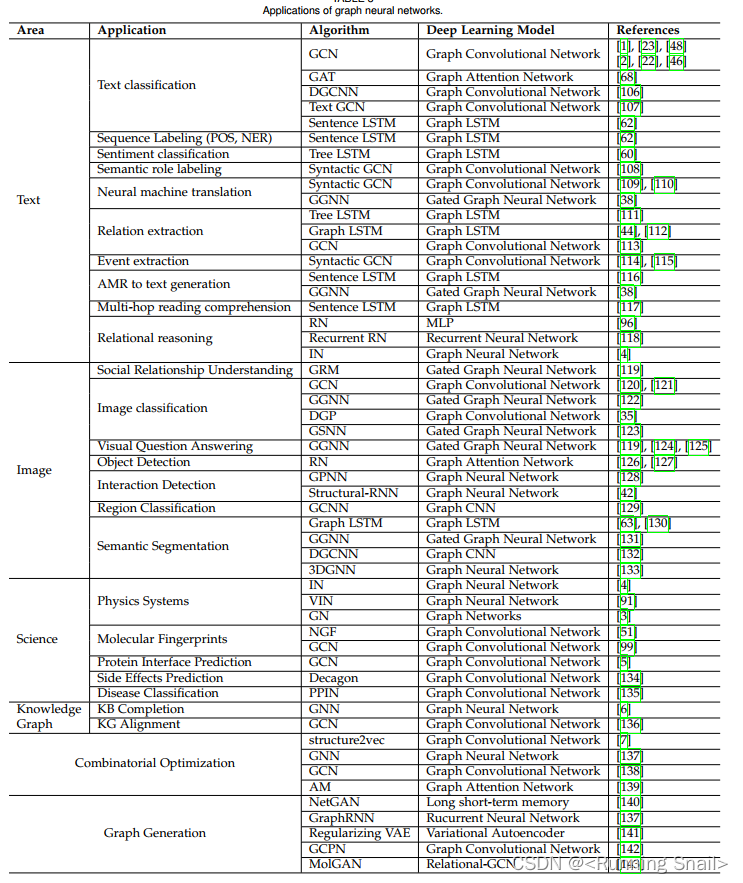
图神经网络基础

图基本模块定义

三个特征：

• 点–特征向量表示
• 边–表示关系（分有向/无向）
• 图—图向量（全局）

无论事整的多么复杂，我们利用图神经网络的目的就是整合特征，重构特征
目的：做好点特征，边特征，最后做好整体的图特征。借助图结构把这些特征做好（点、边、全局的）embedding
输出结果：对点/边/图 做分类、回归

图的邻接矩阵

邻接矩阵：告诉计算机每个点的邻居都有谁

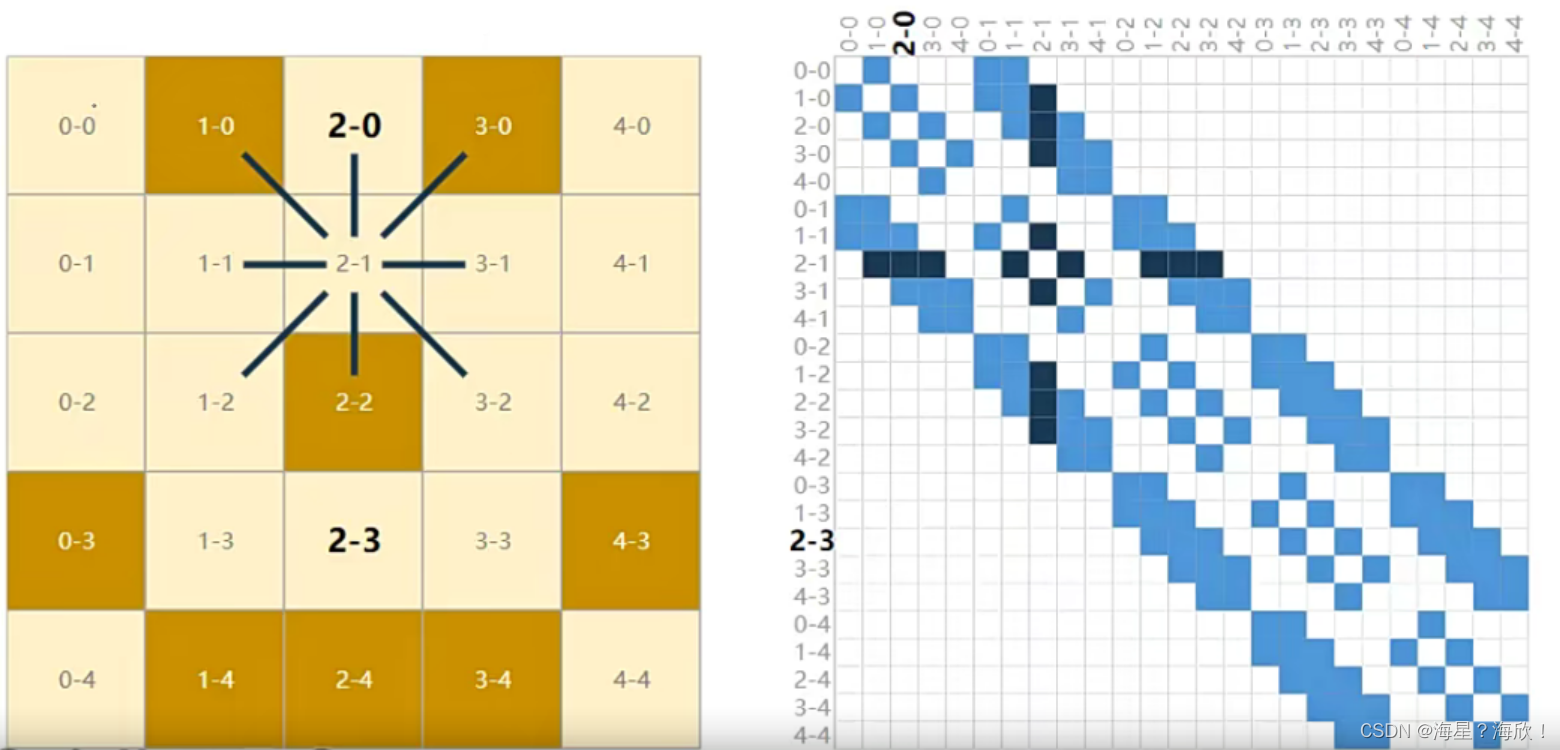
有连接关系的标1，无关系的标0.
双向边的邻接矩阵对称的
GNN（A，X）传入模型中，邻接矩阵，点的特征

文本数据也可以表示图的形式，邻接矩阵表示的连接关系

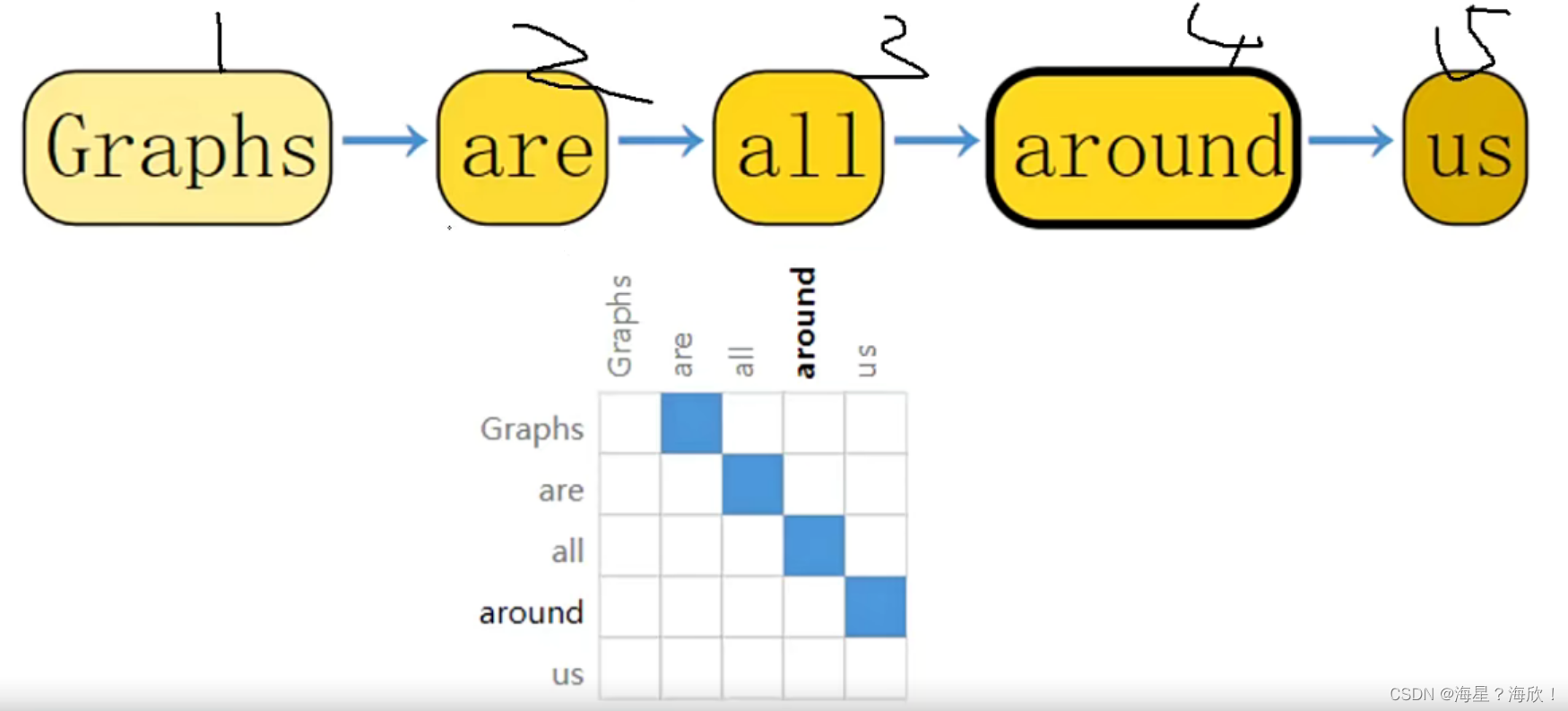
蓝色表示1，白色表示0，比较稀疏的矩阵。
注：在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵

邻接矩阵在代码中传入的一般不是N * N的，而是2 * N

[source,target]：从。。到。。

点特征的更新（重构）

点的更新，不仅考虑自身信息，也考虑邻居的信息
结合邻居与自身信息：

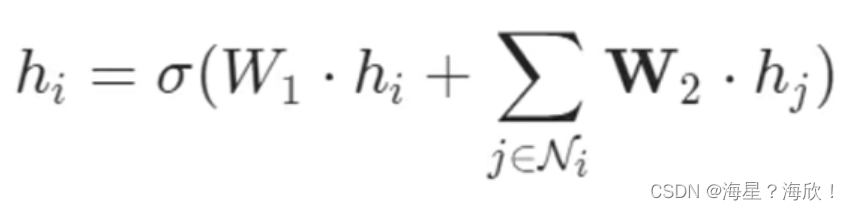
sigam激活函数，w权重，可学习的权重参数
聚合操作可以当作全连接层，更新的方法有很多，可以自己设置（求和，求均值，最大，最小）

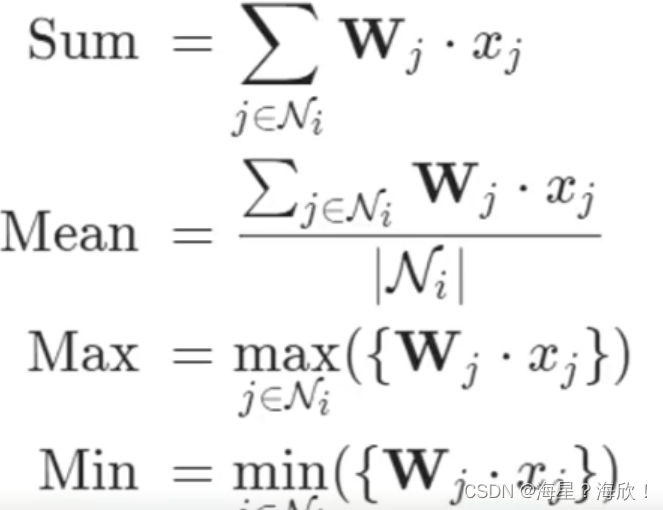
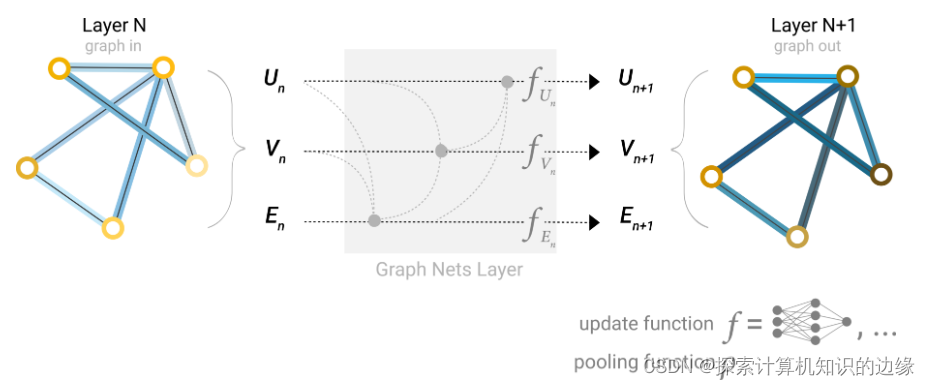
多层GNN

GNN也可以有多层：

• GNN的本质就是更新各部分特征
• 其中输入是特征，输出也是特征，邻接矩阵也不会变的
  
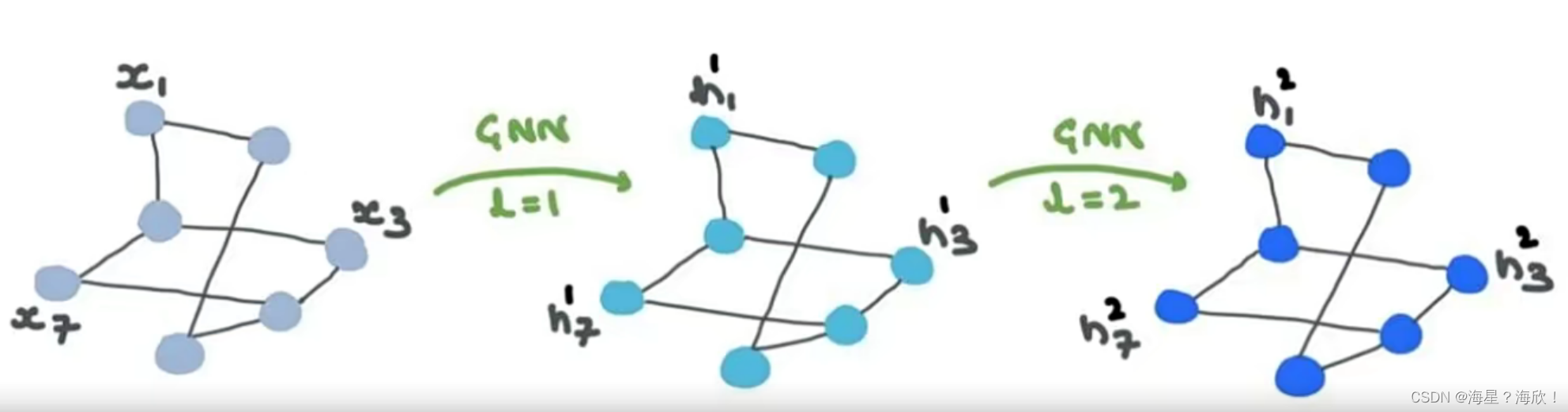
  原始输入–第一次结果–第二次结果
  图结构与邻接矩阵不变，在变的是点特征

感受野：随着卷积的进行，每个点能感受到的区域越来越大

图卷积GCN模型

图中常见任务：

• 节点分类，对每个节点进行预测，不同点是否有连接预测
• 整个图分类，部分图分类等，不同子图是否相似，异常检测等
• GCN归根到底还是要完成特征提取操作，只不过输入对象不需要是固定格式

通常交给GCN两个东西就行：1.各节点输入特征；2.网络结构图
交给图神经网络，用损失函数去迭代去更新

GCN并不是纯的有监督学习，这个也是GCN优势：不需要全部标签，用少量标签也能训练。
计算损失时只用有标签的（交通预测中，偏远地区没有人工标签数据）
要让某一个点的损失小，那么它的邻居也要损失小，所以适合做半监督问题。

GCN基本思想

针对橙色节点，计算它的特征：平均其邻居特征(包括自身)后传入神经网络：
如何重构/更新黄色点：先聚合综合（平均）— 经过神经网络，即加上可训练参数—得到两维向量

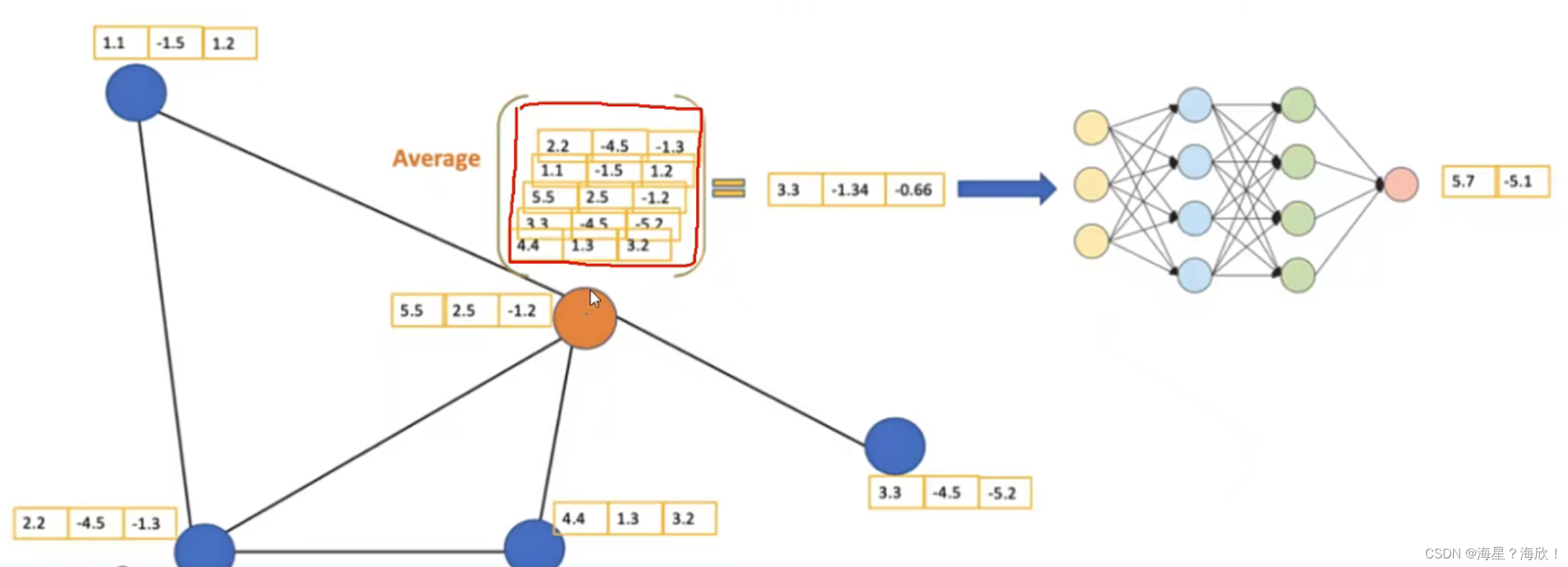
网络层数：

这个跟卷积类似，GCN也可以做多层，每一层输入的还是节点特征
然后将当前特征与网络结构图继续传入下层就可以不断算下去了

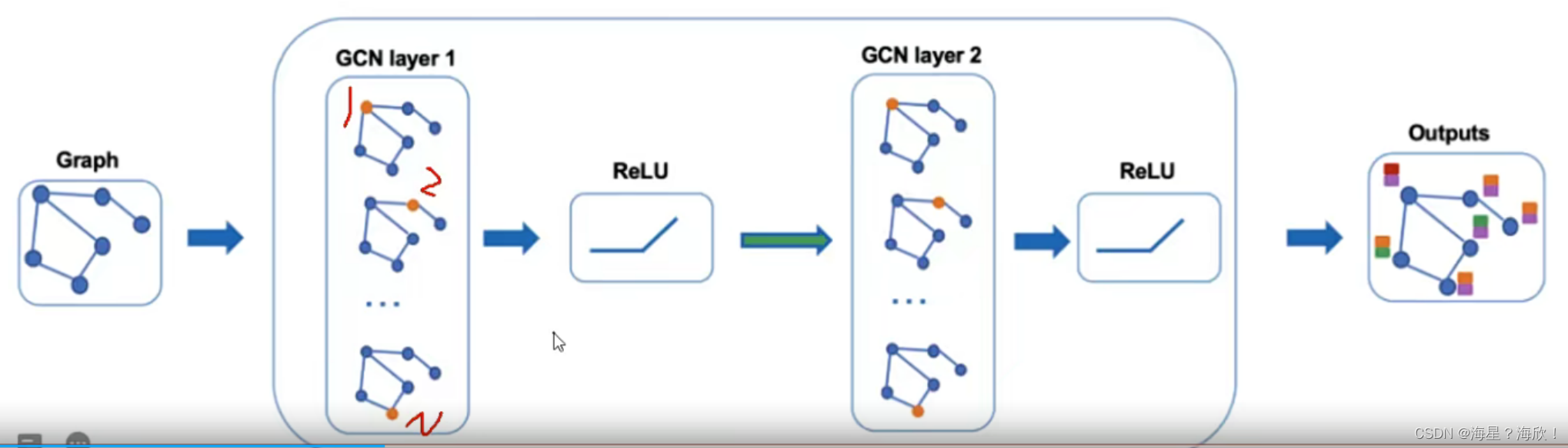
原邻接矩阵–每个点更新–激活函数RELU— 第二次更新–激活函数RELU—经过图卷积的洗，最后得到每个点对应的向量。

但一般不用做太多层（通过6个人可以认识任何一个人），上图栗子中，做两次就能看到其余所有点。

基本计算

图中基本组成：
G就是咱们的图
A是邻接矩阵
D是各个节点的度
F是每个节点的特征

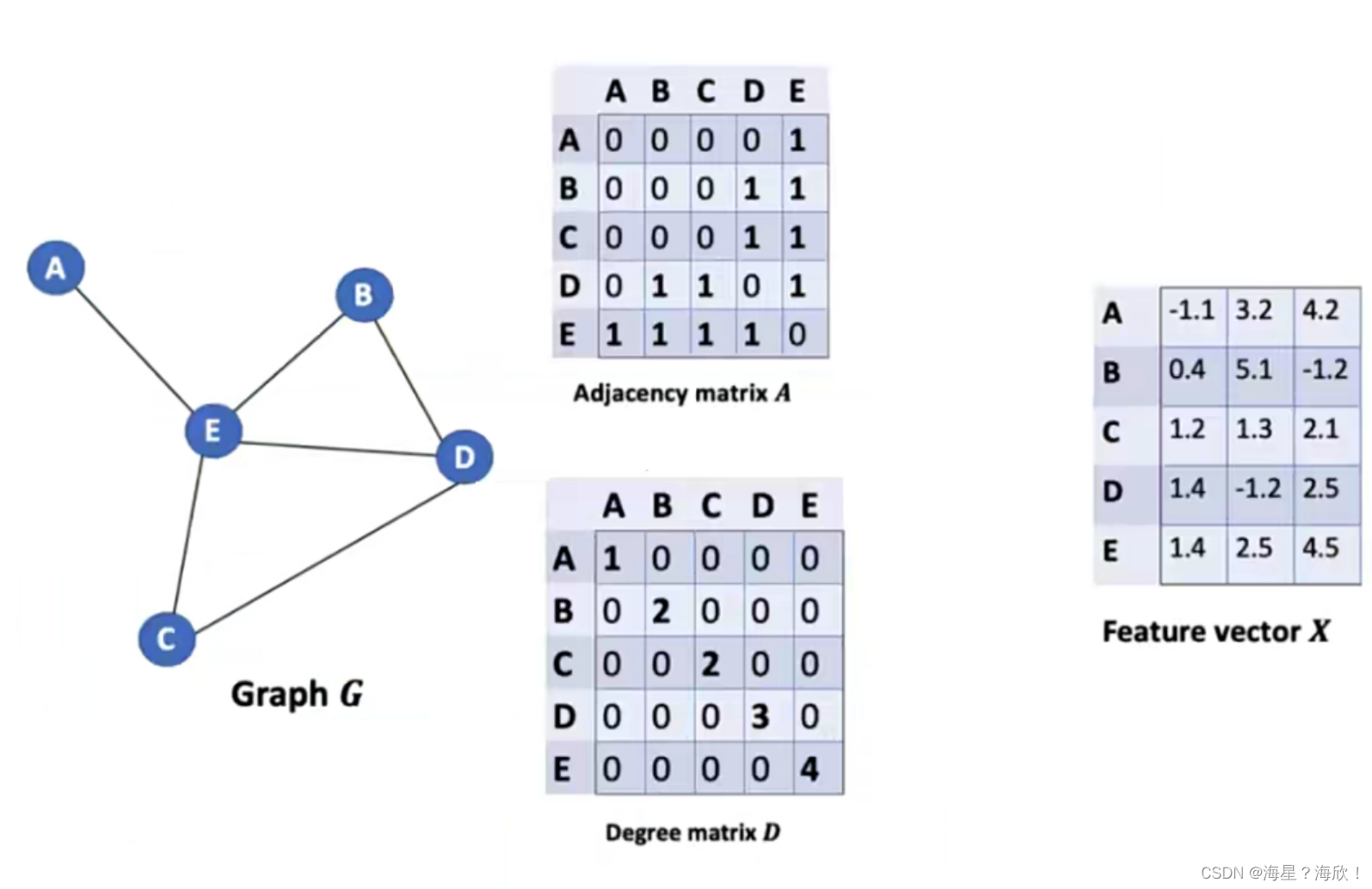
特征计算方法：其实就是邻接矩阵与特征矩阵进行乘法操作，表示聚合邻居信息

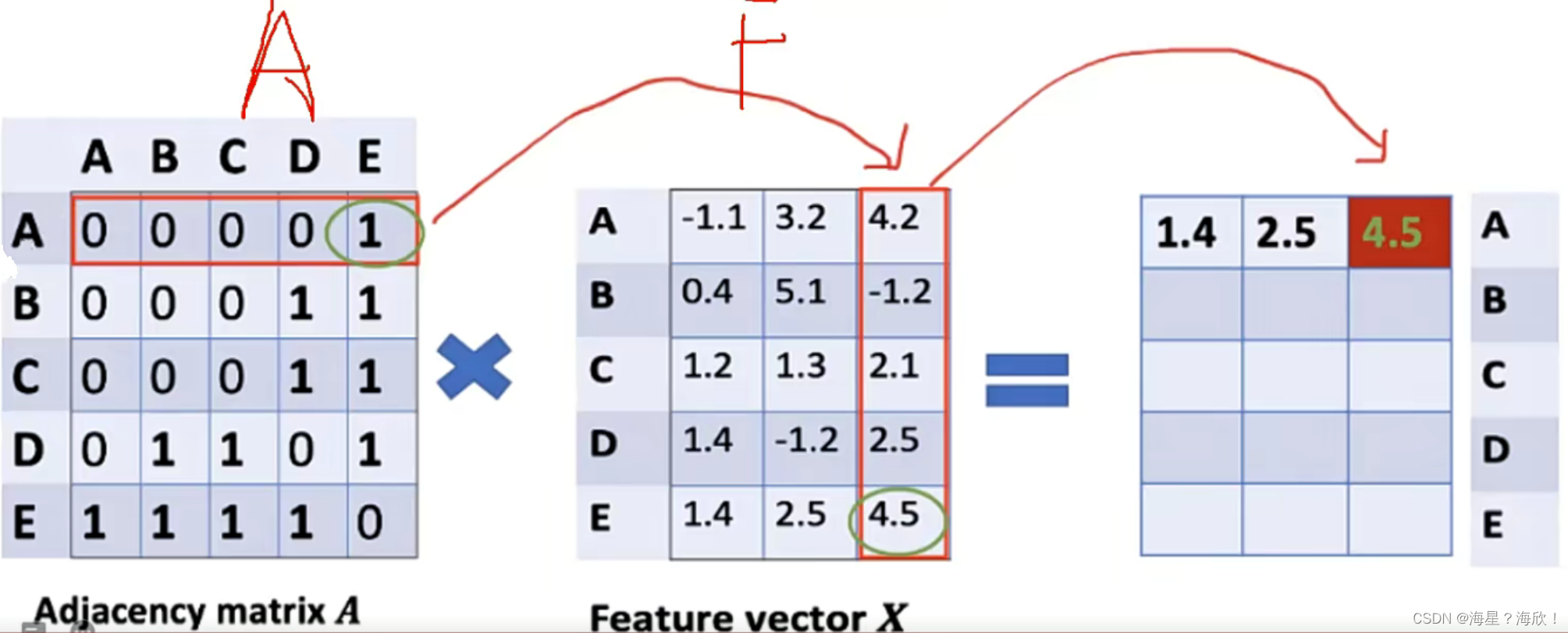
问题1：光想着别人，没考虑自己呢。


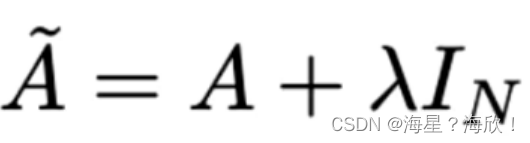
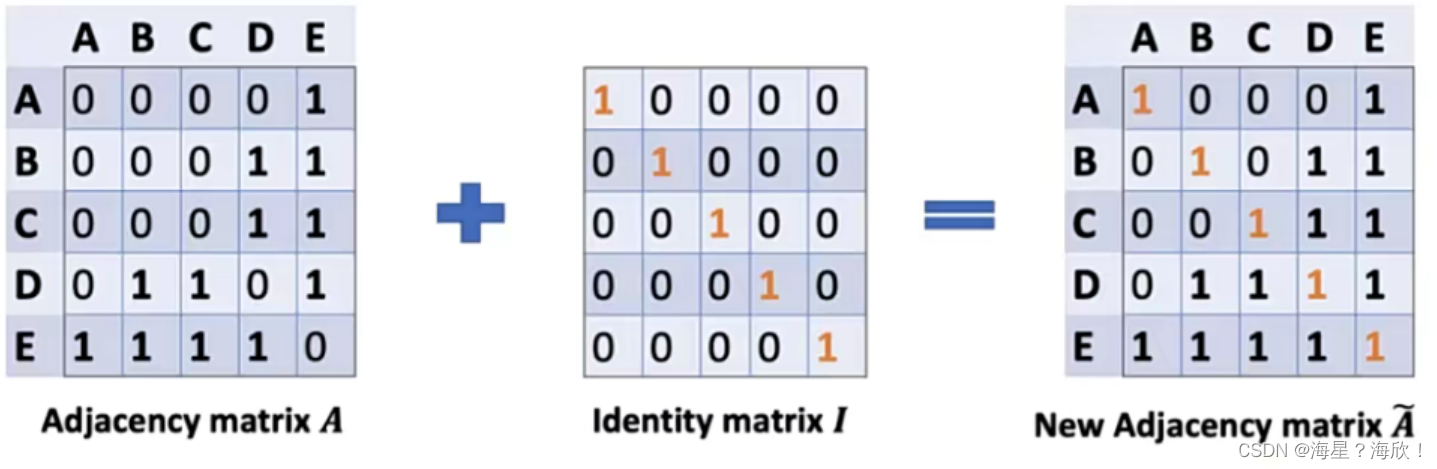
问题2：只考虑了加法，没考虑平均
其实就是对度矩阵乘以度矩阵D的逆矩阵，这样就相当于平均的感觉了

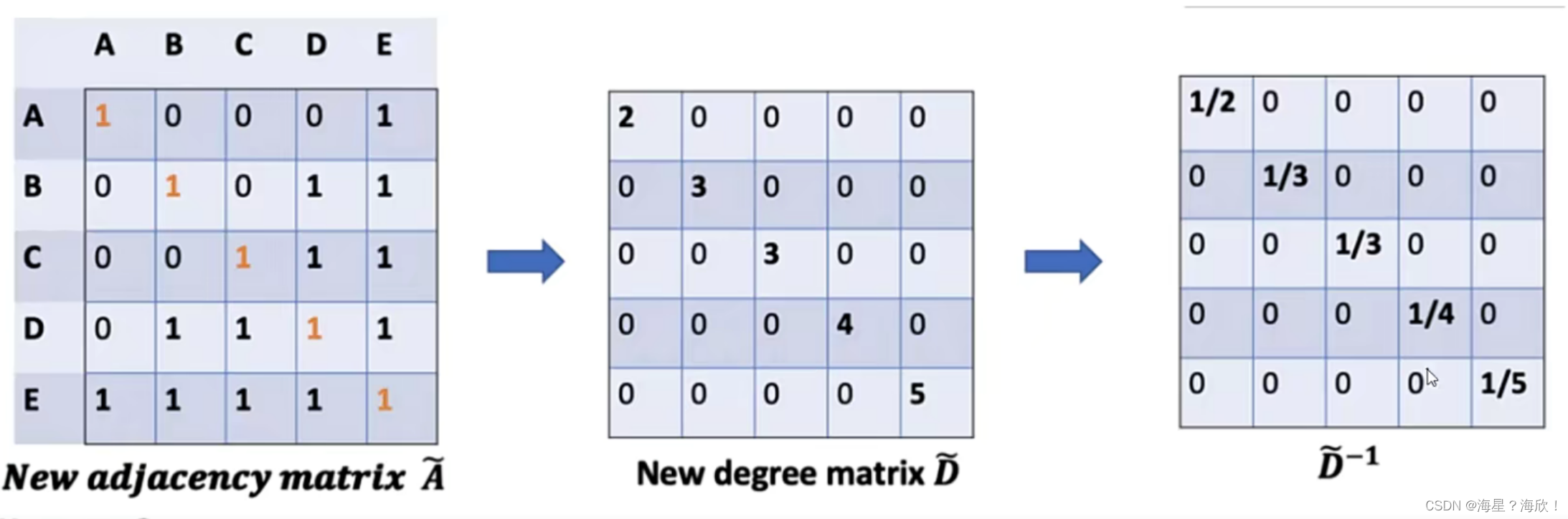
这里1/2相当于是对第一行做归一化操作，列也应该做归一化：

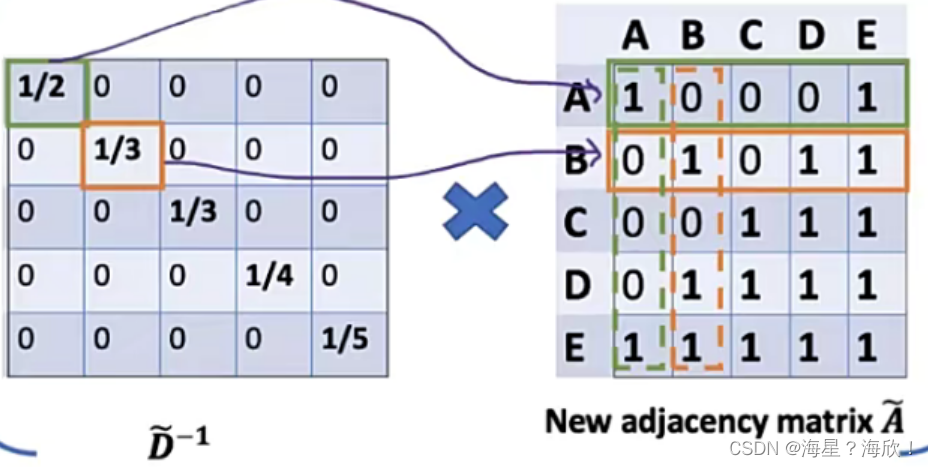
这样相当于归一化了两次，数导致更小了，应该开一个根号：

为什么这样做：
下面的小红和小绿，A和B两个人的度都要考虑进来，


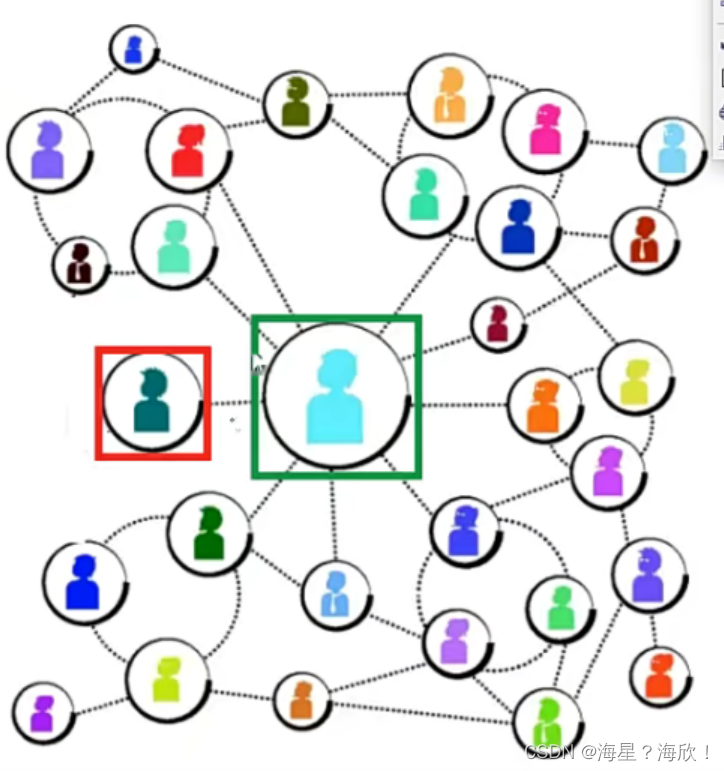
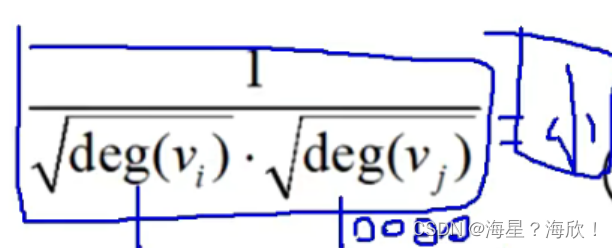
因为小绿的度大会把其关系的权重变的很小，造成对小红的影响没有那么大。

最终公式：
例如完成一个十分类任务的，F就为10表示输出层

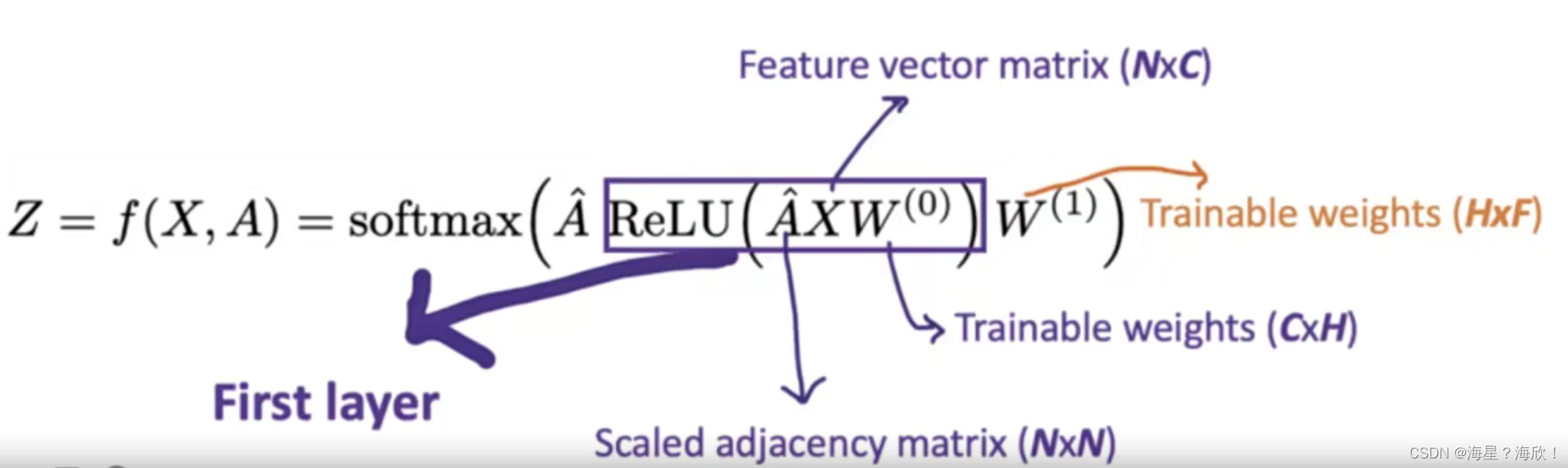
第一层：邻接矩阵，重新组合特征X，做一组预设乘上权重参数，套上激活函数relu
第二层：一样的

其中邻居矩阵是更新过的，

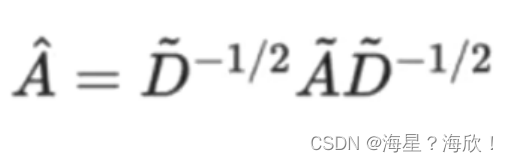
GCN的层数：
理论上来说肯定越大越好
但是实际的图中可能不需要那么多
在社交网络中，只需6个人你可以认识全世界
所以一般的GCN层数不会特别多
经过实验：在多个图数据集中，都发现两三层的比较合适，多了反而变差

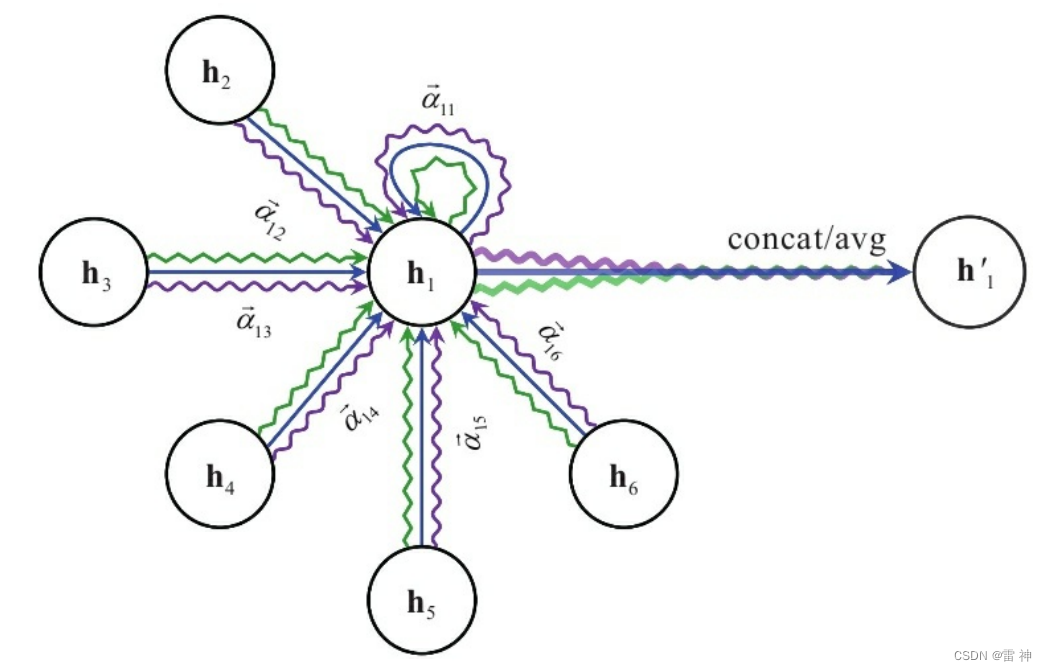
图注意力机制graph attention network

哪个节点影响大，哪个节点影响小，需要权重来区分
栗子：5个点，每个点是四维数据。
通过权重来区分影响大小，2，3点对1的影响是否应该一样？


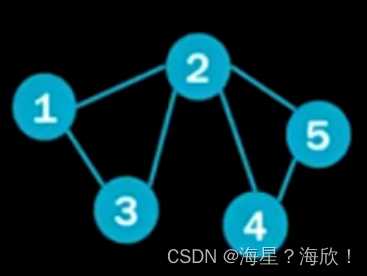
邻接矩阵[5×5] :N×N
特征矩阵[5×4] :5个点，每个点是四维数据。
可训练权重参数w[4×8]
聚合更新：[5,8]

这是前面的内容，这一节主要是引入一个权重项

公式：

hi，hj：点i与点j的特征
w:可训练的权重参数，先进行维度映射
拿到两个特征后，做内积—来体现权重值
a:指attention
softmax：归一化，2对1的权重和3对1的权重，之和要为1
exp(eij)：指对eij做e^x 的幂次映射，让结果差异大一些

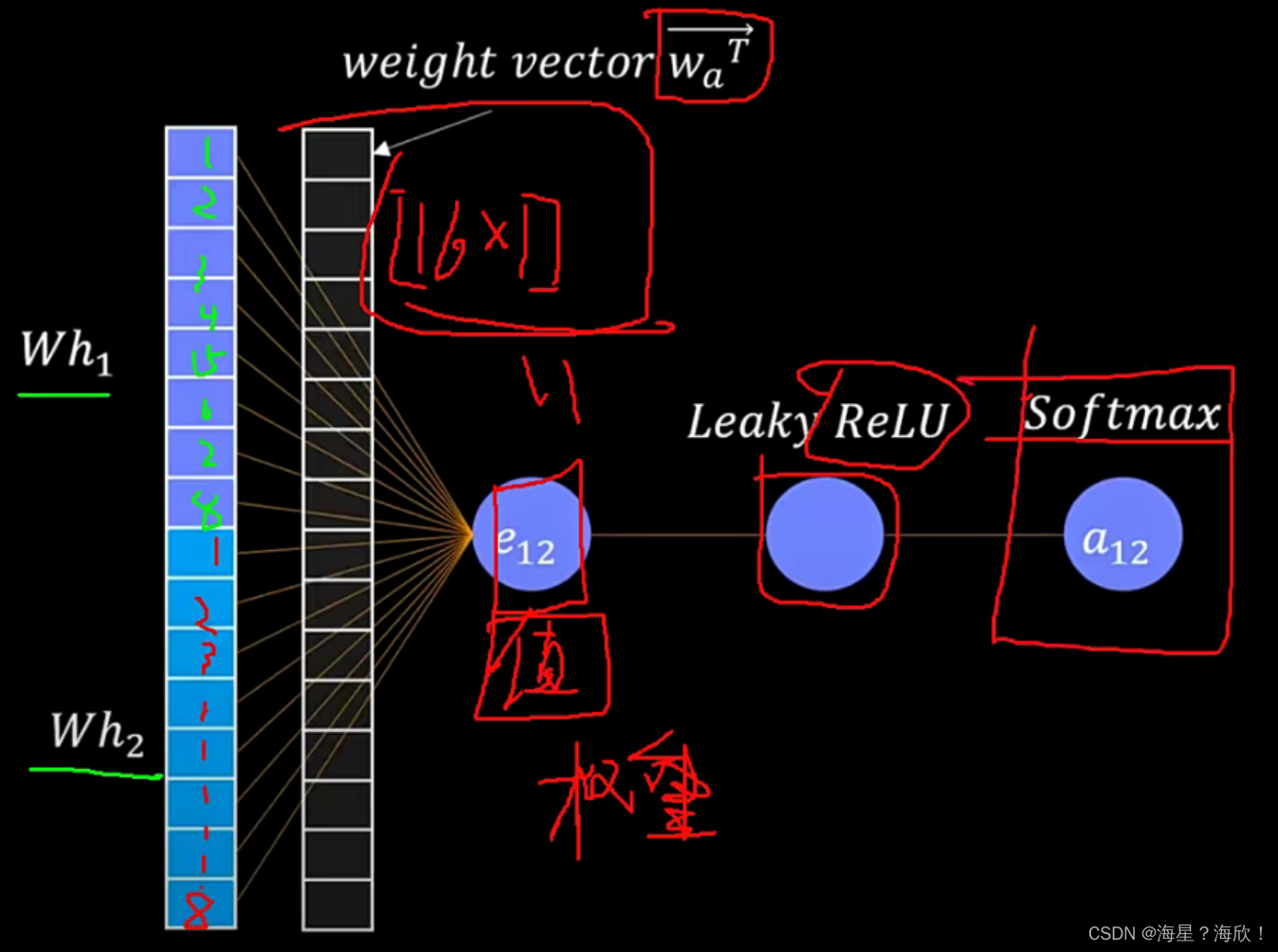
残留问题：a的计算

1×5维特征向量，称上一个5×8的向量，变成8维向量。并拼接
加入一个可训练可学习的权重参数矩阵
再称一个16×1的矩阵，得到一个值，作为我们的权重.
因为权重要为正值，加上relu激活函数，
最后归一化一下

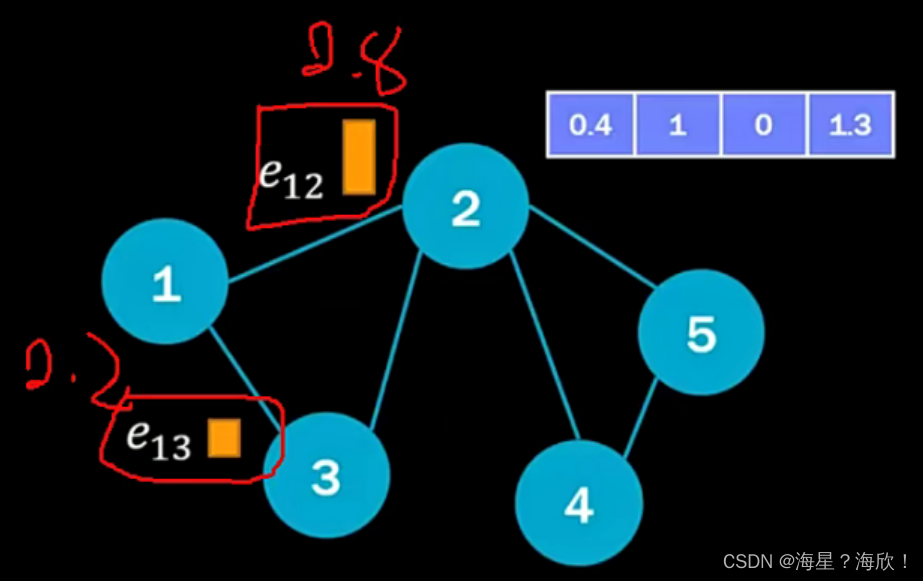
attention其实就是对邻接矩阵进行了加权，多加了一次处理
1对2的权重e12，其实改的就是邻接矩阵中a12处的数值。

T-GCN序列图神经网络

有些图随时间变化而变化
1，随着时间变化，点的特征在变
2，随着时间变化，点的特征在变，图结构也在变
套进RNN中
应用：疫情蔓延图，交通流量随时间变化

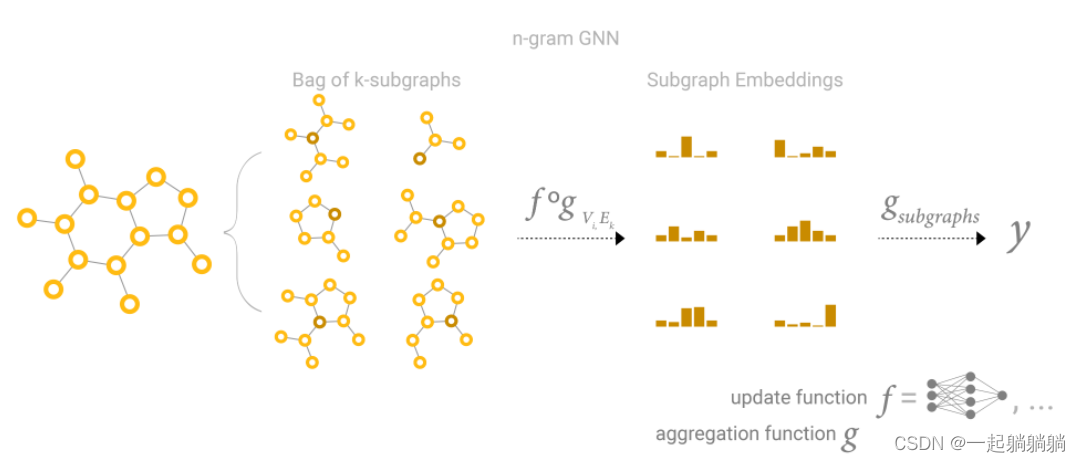
图相似度

论文链接

输入：两个/多个图结构
输入到图神经网络
输出：进行匹配相似度，输出得分