一、 需求分析

0.问题描述

在数学上，一个一元n次多项式 可按降序写成：

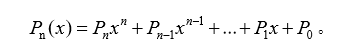
它由n+1个系数唯一确定，因此，在计算机里他可以用一个线性表表示：

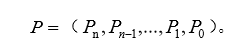
设Pn(x)和Qn(x)分别为两个一元多项式，请求出两个一元多项式的加法运算的结果，要求元素按照多项式的次数递减的次序排列。

1.问题分析

需求：实现两个一元多项式的加法运算。
实现功能：①通过键盘接收输入的整数（浮点数）
②以系数和指数对应的形式，储存到计算机内存中
③实现一元多项式的加法运算
④通过屏幕输出一元多项式加法运算后的结果

2.输入数据

分别输入两组二元组数据，每一组二元组数据分别代表一个多项式，每个二元组包含两个整数（一个浮点数和一个整数），第一个整数（浮点数）代表多项式的项的系数，第二个整数代表该项的次数（指数），且在输入过程中，要求同一个多项式中不能出现两个项的指数相同。（使用模板设计，以下设计以系数为整数为例）

3.输出数据

输出两个一元二次多项式相加运算之后的结果，形式如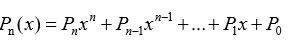

4.测试样例设计

（1）样例输入1：

4
3 2
4 5
1 1
2 3
3
-3 2
-4 5
2 4

（1）样例输出1：

第一个多项式为:
4x^5+2x^3+3x^2+1x^1
第二个多项式为:
-4x^5+2x^4-3x^2
两个多项式的和为:
2x^4+2x^3+1x^1

目的：本例为了测试在两组多项式相加时，两个多项式中恰有相同指数项的系数互为相反数，即相加之后为0，能否实现正确计算。

（2）样例输入2：

2
0 1
2 3
3
2 6
3 9
4 3

（2）样例输出2：

第一个多项式为:
2x^3
第二个多项式为:
3x^9+2x^6+4x^3
两个多项式的和为:
3x^9+2x^6+6x^3

目的：本例为了检测若输入的项的系数是0，那么输出是否会出现错误，会不会把项 为0的也输出出来，能否实现正确运算。

（3）样例输入3：

1
2 3
1
3 3

（3）样例输出3：

第一个多项式为:
2x^3
第二个多项式为:
3x^3
两个多项式的和为:
5x^3

目的：本例为了测试在两组多项式只有一项的情况下，并且这项的幂相等，观察输出是否是一项。

（4）样例输入4：

2
0 5
0 4
5
6 5
3 8
-2 2
3 1
2 4

（4）样例输出4：

第一个多项式为:
（此处输出为空）
第二个多项式为:
3x^8+6x^5+2x^4-2x^2+3x^1
两个多项式的和为:
3x^8+6x^5+2x^4-2x^2+3x^1

目的：当某一个多项式所有项的系数均为0时，观察该多项式样式输出 及运算结果。

（5）样例输入5：

3
4 2
-2 2
-1 2
2
0 2
6 2

（5）样例输出5：

第一个多项式为:
4x^2-2x^2-1x^2
第二个多项式为:
6x^2
两个多项式的和为:
10x^2-2x^2-1x^2

目的：本例是反例，若不符合要求同一个多项式不能有相同的幂的项存在，观察该多项式输出及运算结果。

二、概要设计

1.抽象数据类型

问题的输入为多项式的，多项式由一个或者多个项构成，而每个项又是由一个指数和一个系数唯一确定，那么这个指数和这个系数就是一个具有关系的数对，我们可以用结构体进行存储，可以形象的定义为一个二元组（ai，bi），那么这些二元组按照多项式的次数递减的次序排列，则具有线性关系，则两个多项式可以分别用两个线性表表示，线性表中的数据元素即为多项式的项的二元组。

数据对象：

数据关系：

因为多项式按照多项式的次数递减的次序排列，相应的指数对应的系数也就排列好前后位置，因此具有线性结构，这些二元组之间都存在着有序的关系。即

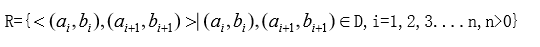
基本操作：

①	link();                       // 构造线性表 
②	~link();                      // 摧毁线性表 
③	void init();                  // 初始化线性表 
④	void next();                  // 当前位置后移 
⑤	void movetostart();           // 移动当前位置到线性表表头 
⑥	arrary<E> getvalue();         // 获取当前位置存储单元内的数据元素
⑦	void insert(arrary<E> elem);   // 插入数据元素（实现线性表的有序性） 
⑧	int getsize();                // 返回线性表长度
⑨	void change(arrary<E> elem);  // 改变储存数据元素的值

2.算法的基本思想

存储：解决本问题首先要想到的就是怎么把一个乱序输入的二元组按照第二个数的从大到小的顺序排列下来，可以这么想，每次要添加一个二元组的时候都要把已经存在的二元组进行一次从头的搜索，查找到一个适当位置，使得二元组插入后，线性表数据元素满足以二元组第二个数依次递减的次序排列。把二元组的前后逻辑线性关系存储在链表中，通过修改插入函数实现上面存储中所提到的查找位置问题，然后把输入的二元组插入即可完成有序链表的构建。
相加：把第二个多项式的线性表中的每一个数据元素二元组中第二个数依次与第一个多项式的线性表中的每一个数据元素二元组中第二个数比较，如果相同，通过修改第一个多项式的线性表中的每一个数据元素二元组中第一个数，实现相同指数项的相加，否则通过插入操作把该二元组插入到第一个多项式的线性表中。
输出：完成相加后，计算结果储存在第一个多项式的线性表中，且由于插入时已完成了有序性的排列，按照线性表的线性顺序及多项式的写法规则输出完成相加后第一个多项式线性表中的数据元素。

3.程序的流程

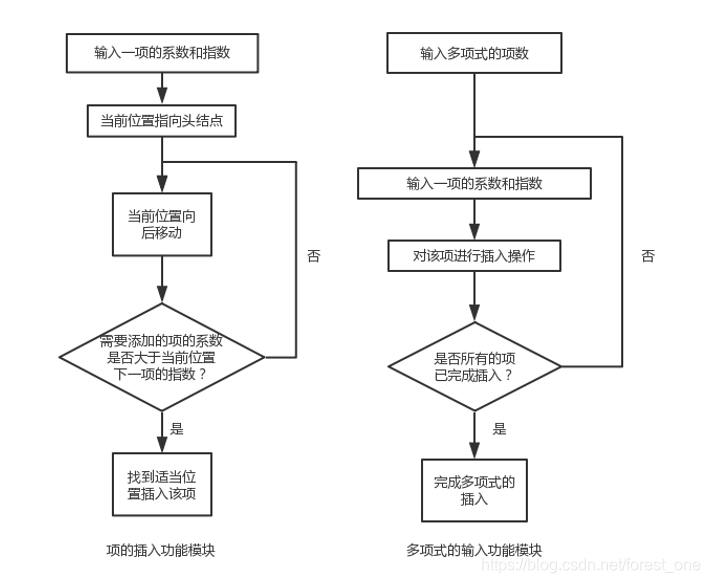
① 第一个模块：输入模块。提示输入多项式的项数，之后提示输入多项式的每一项的系数和指数，调用insert（有序插入）等基本操作实现有序存储数据，将多项式分别储存到线性表中，然后根据多项式的写法规则调用基本操作进行打印多项式。
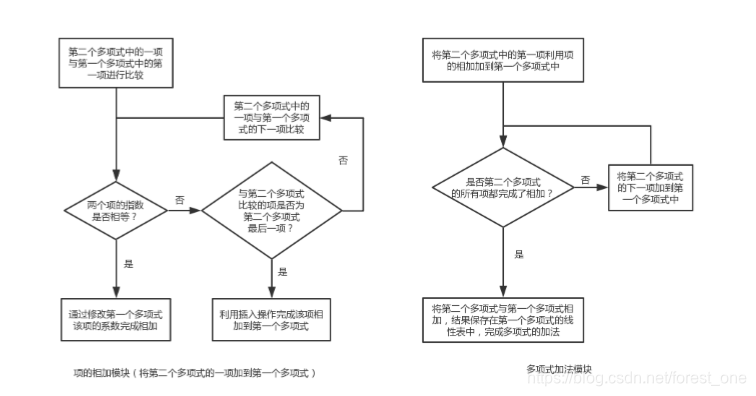
② 第二个模块：计算模块。根据第一个模块接受的数据，利用多重循环，对第二个多项式与第一个多项式进行遍历比较，并调用change、insert等基本操作完成两个多项式的相加，计算结果存储到第一个多项式的线性表中。
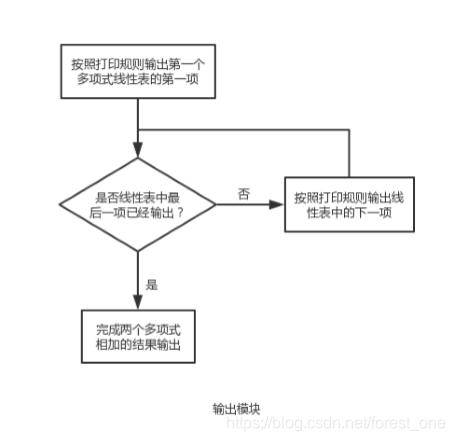
③ 第三个模块：输出模块。通过提示，按照多项式的写法规则打印出相加后的多项式的形式。

三、详细设计

1.物理数据类型

多项式的系数为整数（浮点数），指数为整数，所以物理数据类型可以为int等（采用模板）。
多项式的项按照指数从大到小排列，相加运算时会改变项的个数。选用基于链表实现的线性表。
① 结点SNode的构造：结构体SNode在这个题中要存储的是一个多项式的项，其包含两个元素，多项式的系数和指数，所以我添加了一个结构体arrary作为一个二元组，包含系数（value），指数（element）将这个结构体类型的元素作为结点的数据元素
伪代码：

struct arrary{E value;E element;
};struct SNode {arrary<E> elem;SNode *next; 
};

② 基本操作：基于有序链表实现线性表ADT，要进行的基本操作有：
Ⅰ构造线性表
伪代码：

link()
{ init();}

Ⅱ摧毁线性表
伪代码：

~link()
{removeall();}

流程：通过link类的一个私有函数removeall完成操作。

Ⅲ初始化线性表

伪代码：

void init(){curr=tail=head=new SNode<E>;linksize=0;}

Ⅳ把当前位置从前到后移动一个存储单元。
伪代码：

void next()
{if(curr!=tail)curr=curr->next;
}

流程：当前位置移动到下一个节点，只要把当前位置的指针curr的指向修改为他所指向的节点中的指针next的指向就可以做到，但是要注意表尾操作。
Ⅴ移动当前位置到线性表表头。
伪代码：

void moveToStart()
{curr=head;}

流程：把头节点的存储地址的值赋值给当前位置curr就可以实现当前位置头置。
Ⅵ获取当前位置存储单元内的数据元素。
伪代码：

arrary<E> getvalue()
{return curr->elem;}

流程：函数返回当前位置指向的节点中包含的数据元素。

Ⅶ向线性表插入一个数据元素（有序线性表的实现函数）。

伪代码：

void insert(arrary<E> elem){for(curr=head;curr!=tail;curr=curr->next){if(temp.element>curr->next->elem.element)break;}SNode<E>* tempnew =new SNode<E>;tempnew->elem.value=temp.value;tempnew->elem.element=temp.element;tempnew->next=curr->next;curr->next=tempnew;if(tail==curr)tail=curr->next;linksize++;}

流程：首先把当前位置设定在头指针的位置，之后开始用函数参数elem的element和当前位置的数据元素（也就是栅栏后面的节点的二元组中的第二个数）比较大小，如果找到了一个位置使得后面的节点中的指数小于要输入的节点的指数那么终止循环，如果没找到这样的位置，说明输入的项指数比已经有的所有项都要小，那么就会把这个位置定在表尾，之后让当前位置所指节点的next指针指向新的节点，也就是存储新项的地方，新节点的前两个参数就是函数的两个参数，指针肯定指向下一节点，若新节点是最后一个节点，也就是他存储的项的指数最小，那么要让表尾指针指向新节点 ，同时链表长度加一。

Ⅷ 获取线性表的长度。

伪代码：

int getsize(){return  linksize;}

流程：在每一次进行插入等操作时，都会有一个变量linksize发生变化，它记录了链表的节点数目，函数返回他就可以得到线性表长度。

Ⅸ修改当前存储单元的值。

伪代码：

void  change(arrary<E> temp){curr->elem.value=temp.value;curr->elem.element=temp.element; }

流程：为了实现两个多项式相加的操作同时又不影响链表的通用性，那么将需要修改的数据元素的值作为函数的参数，把原来的节点中的value系数和element指数全部修改为函数的参数。

2.输入和输出的格式

输入：
① 开始提示“请输入第一个一元多项式的项数:”，提示输入一个整数，之后提示"接下来 n行，分别输入每一项的系数和指数，如：3 2（其中3为系数，2为指数，中间以空格分隔）"。完成输入第一个多项式。
② 然后提示“请输入第二个一元多项式的项数:”，提示输入一个整数，之后提示"接下来 n行，分别输入每一项的系数和指数，如：3 2（其中3为系数，2为指数，中间以空格分隔）"。输入第二个多项式的输入。
输出：
① 提示"第一个多项式为:"，之后打印第一个多项式多项式的排布，打印之后输出一行分隔符。
② 提示"第二个多项式为:"，之后打印第二个多项式多项式的排布，打印之后输出一行分隔符。
③ 提示"两个多项式的和为:"，之后打印两个多项式相加并存入第一个多项式线性表后的结果。

3.算法的具体步骤

（1）模块分析：

①第一个模块
【1】第一个多项式的输入和输出：
Ⅰ通过一个n代表第一个多项式的项数的输入进入第一个多项式的每一项系数和指数的输入，调用修改的插入函数实现数据的存入。

cin>>n;
cin>>temp.value>>temp.element;
a.insert(temp);

Ⅱ通过调用movetostart先把当前位置移动到表头，之后从头往后依次处理每个存储位置，特殊处理第一个输出还有系数为0的输出，调用getvalue和getelement实现输出。

a.movetostart();
a.getvalue();

【2】第二个多项式的输入和输出
Ⅰ通过一个m代表第二个多项式的项数的输入进入第二个多项式的每一项系数和指数的输入，调用修改的插入函数实现数据的存入。

cin>>n;
cin>>temp.value>>temp.element;
b.insert(temp);

Ⅱ通过调用movetostart先把当前位置移动到表头，之后从头往后依次处理每个存储位置，特殊处理第一个输出还有系数为0的输出，调用getvalue和getelement实现输出。

b.movetostart();
b.getvalue();

②第二个模块（实现多项式的加法运算，并将结果保存到第一个多项式的线性表中）：首先对存储第二个多项式的线性表进行从头到尾的元素遍历，每一个第二个多项式中的元素都要再分别遍历第一个多项式中的元素，若查找到指数相同的项，那么调用change把第二个多项式中的系数加到第一个多项式中，如果没有找到，那就直接调用insert函数实现存入。
b.movetoStart();
a.movetoStart();
如果查找到：

if(b.getvalue().element==a.getvalue().element)
{       arrary<int> temp2;temp2.value=a.getvalue().value+b.getvalue().value;temp2.element=a.getvalue().element;
a.change(temp2); 
}

如果没查找到那么：

arrary<int>temp;
temp.value=b.getvalue().value;
temp.element=b.getvalue().element;
a.insert(temp);

③第三个模块（输出两个多项式相加的结果）：和前文输出方法一致，通过调用movetoStart先把当前位置移动到表头，之后从头往后依次处理每个存储位置，特殊处理第一个输出还有系数为0的输出，调用getvalue和getelement实现输出。

a.movetoStart();
a.getvalue();

流程图：
第一个模块：

第二个模块：

第三个模块：

4.算法的时空分析

第一个模块：对于第一个多项式的输入，首先要输入n个数对，存储时每个数对都要对已有的链表元素遍历一次，输入操作的时间代价根据化简规则略去低阶项和常数项，得到输入时间代价是Θ(n²)；输出是从头到尾依次输出，所以时间代价是Θ(n)，所以，输入并打印第一个多项式的时间代价是Θ(n²)；与第一个多项式相同输入第二个多项式，所以第二个多项式输入并打印的时间代价是Θ(m²)；综上，第一个模块的时间代价是Θ(max{ n²,m² }）。
第二个模块：在对应多项式A，多项式B的每一个值都去遍历一次，这个双重嵌套for循环的时间代价为Θ(nm),之后进入一个也在第一重for循环中的if解决是否要用到插入操作，那么这个语句的时间代价是Θ(n²)。
所以总共的时间代价是Θ(max{nm,n² }）。
第三个模块:假设两个多项式相加之后的第一个多项式的长度为x，那么输出A的时间代价就是Θ(x)，第四个模块的时间代价就是Θ(x)。
综上所述：整个算法的时间代价就是Θ(max{ nm,n² }）

四、调试分析

1.调试方案设计

调试目的：用手工或编译程序等方法进行测试，修正语法错误和逻辑错误的过程。这是保证计算机信息系统正确性的必不可少的步骤。编完计算机程序，必须送入计算机中测试。根据测试时所发现的错误，进一步诊断，找出原因和具体的位置进行修正。对于本题目，根据调试过程及结果检测两个多项式加法运算相关函数过程及正确性。
样例：（设计样例中的第一个样例）

（1）样例输入1：

4
3 2
4 5
1 1
2 3
3
-3 2
-4 5
2 4

（2）样例输出1：

第一个多项式为:
4x^5+2x^3+3x^2+1x^1
第二个多项式为:
-4x^5+2x^4-3x^2
两个多项式的和为:
2x^4+2x^3+1x^1

调试计划：该样例的设计中两个多项式存在系数互为相反数且指数相同的项，按照设计，当两个多项式进行相加运算时，第二个多项式的项会与第一个多项式中指数相同的项通过函数修改第一个项中对应的元素值，完成相加运算，同时第一个多项式的项数不会改变，及线性表长度不变，观察第一个多项式线性表的长度，验证设计过程的正确性。
设置：在加法运算循环处设置断点，观察调试过程。

2.调试过程和结果，及分析

设置断点：

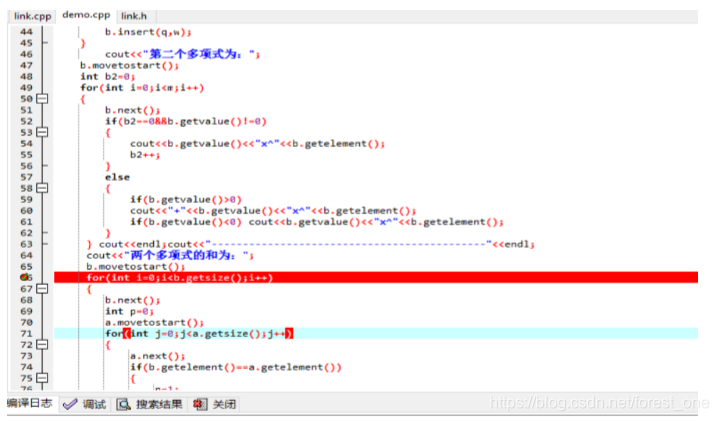
开始调试：
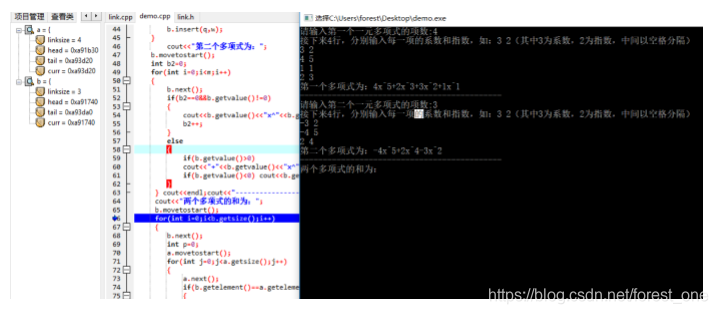
（1）当完成第一个模块输入之后，此时两个多项式线性表的长度均为项的个数，运行正常，结果如下图。

（2）从设置断点进入for循环语句，开始进行两个多项式的相加操作，由于两个多项式的第一个项的指数相同，程序进入if语句，如下图。

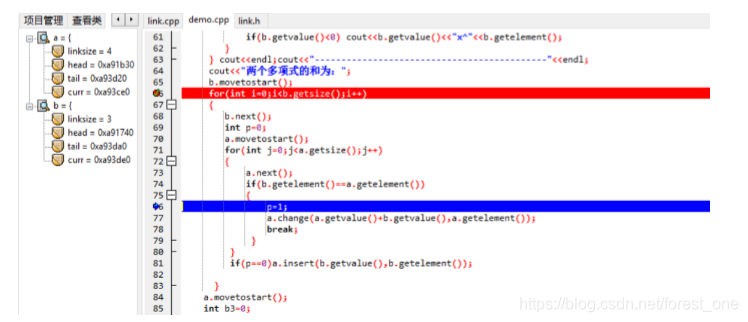
（3）和预测的结果相同，两个项的指数相同完成当前第一个项的相加操作之后，第一个多项式的线性表长度没有发生变化，如下图。

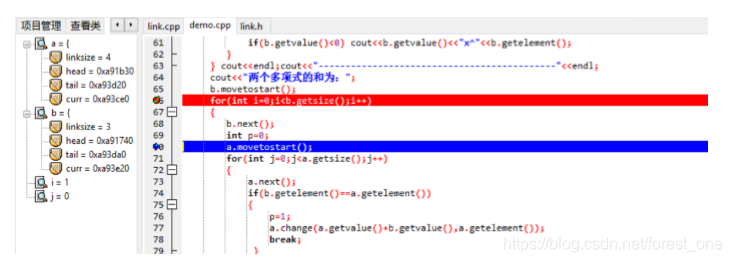
（4）接下来对第二个多项式中的第二项即指数为4的项在第一个多项式中查找，与预测相同，当循环到最后一个时，此时j==3，没有发现相同的项，进入第二个if语句完成插入操作，第一个线性表的长度发生改变，变为5，如下图。

（5）继续进行循环，第二个多项式中的第三项，根据预测与第一个多项式中的第四项相同，会同第一项完成相加时的操作相同，第一个多项式线性表长度不会改变，此时i=2，j=3,调试过程正确，如下图。

（6）完成相加操作后，最后输出第一个多项式，得到两个多项式相加的结果，与预测结果相同，调试结果为正确，如下图。

总结：调试结束，结果与预料一致，说明程序对这组数据的处理没有问题。

五、测试结果

（1） 测试样例1

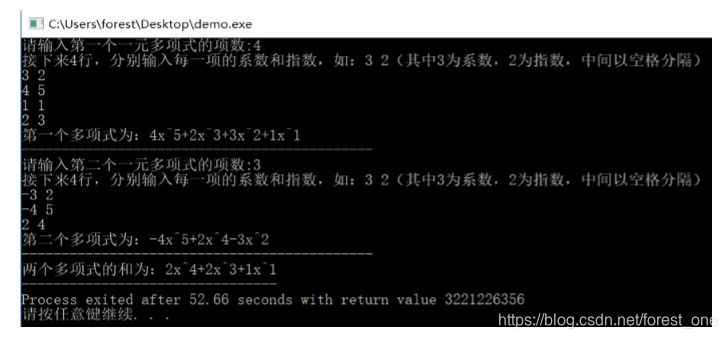
结论分析：两组多项式相加时，两个多项式中恰有相同指数项的系数互为相反数，即相加之后为0，能够实现正确计算。

（2） 测试样例2

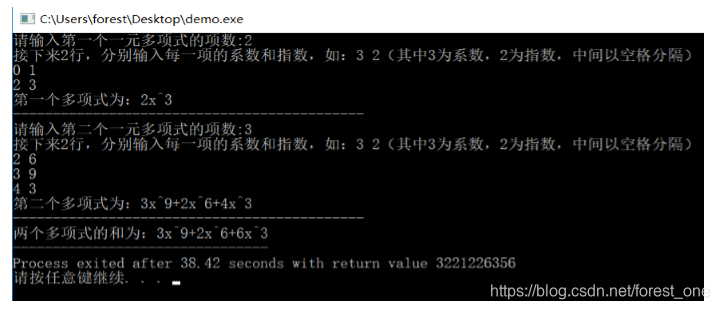
结论分析：输入的项的系数是0，输出未出现错误，不会把项为0的也输出出来，能够实现正确运算。

（3） 测试样例3

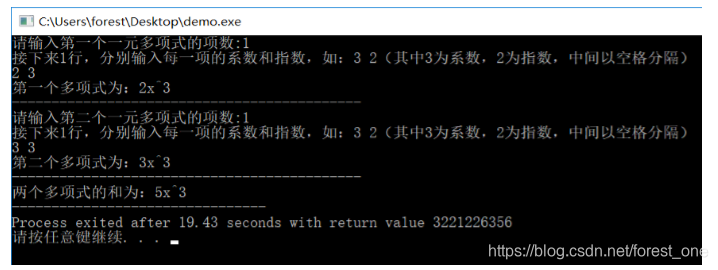
结论分析：在两组多项式只有一项的情况下，并且这项的幂相等，输出为一项，程序计算结果正确。

（4） 测试样例4

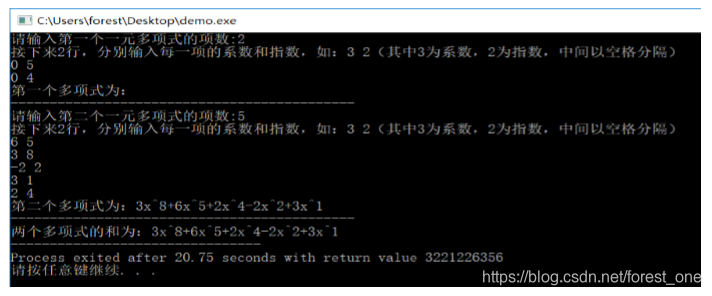
结论分析：当某个多项式所有项的系数均为零时，该多项式不会输出，满足系数为0的项不会输出的设计，最后的计算结果正确，程序运行正常。

（5） 测试样例5

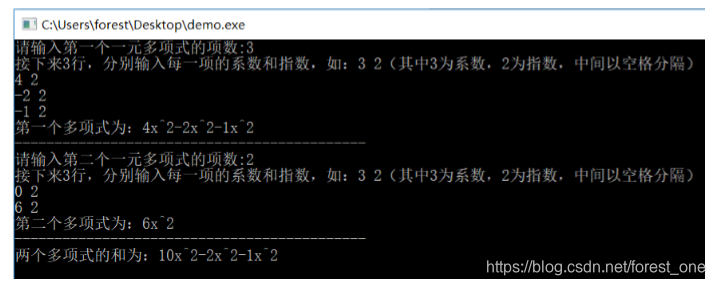
结论分析：本例是反例，若不符合要求同一个多项式不能有相同的幂的项存在，当储存一个多项式时会把指数相同的项当作多个项进行储存，运算时，也会把这些所有项的系数对第一个多项式中的第一个该指数的元素进行操作，完成相加，这也是符合当前该设计的计算过程的，即程序运行正常，由于不符合同一个多项式不能有相同的幂的项存在的要求，输出结果错误。

六、实验日志（选做）

实验时间
2018.10.24-2018.10.30
实验过程
10.24
19：30-21：40
① 完成需求分析模块。
② 完成概要设计模块。
10.25
12：20-15：50
完成详细设计模块。
21：00-22：44
基本完成线性表ADT的设计和实现。
10.26
13：00-17：24
① 完成有序插入基本操作的设计与实现。
② 完成修改储存数据元素的值基本操作的设计与实现。
③ 完成源代码。
10.27
13：00-15：25
完成调试分析模块
10.30
14：30-16：00
针对预备报告进行了完善与修改。
19：30-21：18
① 修改源代码。
② 调试修改后的源代码。
③ 完成最终报告。
实验中遇到的问题及解决分析
(1) 如何实现有序线性表？
分析及解决：对于线性表的有序性，可以通过修改插入基本操作，在插入储存时实现有序储存，即实现了线性表的有序性。
(2）使用模板 template 实现数据对象的多用性。出现报错报错(GCC): error: need ‘typename’ before ‘E::xxx’ because ‘E’ is a dependent scope
分析及解决：通过查询，得知了这样两个概念——
从属名称(dependent names): 模板(template)内出现的名称, 相依于某个模
(template)参数, 如 E t;
嵌套从属名称(nested dependent names):从属名称在 class 内呈嵌套装, 如
E::const_iterator ci;
如果不特定指出 typename, 嵌套从属名称, 有可能产生解析(parse)歧义.
所以，任何时候在模板(template)中指涉一个嵌套从属类型名称, 需要在前一个
位置, 添加关键字 typename;进行如下操作解决了问题
(3）如何实现加法运算？
分析及解决：我们实现这样一个算法过程——遍历操作，每一个第二个多项式中的元素都要再分别遍历第一个多项式中的元素，若查找到指数相同的项，那么调用change把第二个多项式中的系数加到第一个多项式中，如果没有找到，那就直接调用insert函数实现有序存入，完成加法运算。

实验心得
实验设计比较完善，解决了基于有序链表实现多项式的输入输出和相加的功能，但是还是那个反例的问题怎么解决呢，我认为把两个多项式的项逐一存入另一个线性表中是一个好办法，这样的话，根据change函数，在每一次存入多项式的值的时候，新的线性表就构成了一个新的链表，那么就算多项式中有相同指数的项，到了存储进新的线性表中的时候，也会和前面已经存过的指数相同项进行一次系数的相加而不是增多一个节点，但是这个方法每次都要遍历前面已经存储过的节点时间代价有些大是它的缺点。

具体代码实现：
数据结构——一元多项式的加法运算
^{伪代码部分排版有点问题，请见谅！}