何为显著性检验?
显著性检验(significance test)作为判断两个乃至多个数据集之间是否存在差异的方法被广泛应用于各个科研领域。在统计学中,显著性检验是“统计假设检验”(Statistical hypothesis testing)的一种,显著性检验是用于检测科学实验中实验组与对照组之间是否有差异以及差异是否显著的办法。
“无假设,不检验”。用更通俗的话来说就是要先对科研数据做一个假设,然后用检验来检查假设对不对。一般而言,把要检验的假设称之为原假设,记为 H0;把与 H0相对应(相反)的假设称之为备择假设,记为 H1。
如果原假设为真,而检验的结论却劝你放弃原假设。此时,我们把这种错误称之为第一类错误。通常把第一类错误出现的概率记为α;
如果原假设不真,而检验的结论却劝你不放弃原假设。此时,我们把这种错误称之为第二类错误。通常把第二类错误出现的概率记为β。
通常只限定犯第一类错误的最大概率α, 不考虑犯第二类错误的概率β。我们把这样的假设检验称为显著性检验,概率α称为显著性水平。显著性水平是数学界约定俗成的,一般有α =0.05,0.025.0.01这三种情况。代表着显著性检验的结论错误率必须低于5%或2.5%或1%(统计学中,通常把在现实世界中发生几率小于5%的事件称之为“不可能事件”)。
一个通俗简单的例子
黄老板开了两家超市,分别设在不同的地方。现在存在下列数据作为两个超市分部的销售额,集合中的每一个数代表着一年中某一个月的超市销售额。
分店1 = {23,25,26,27,23,24,22,23,25,29,30}
分店2 = {24,25,23,26,27,25,25,28,30,31,29}
现在,黄老板想要知道两家超市的销售额是否有存在明显的差异(是否存在分店1销售额>分店2销售额,抑或反之),以便对接下来超市的战略业务调整做出规划。下属们知道黄老板的难处,纷纷建议“只需要求平均值就知道哪个分部的销售额更大了”。但是作为拥有高学历的黄老板懂得这样一件哲学即“我们生活在概率的世界之中”。那也就意味着,平均值并不能够说明什么问题,即便分店1的销售额平均值大于分店2的销售额平均值仍然不能说明分店1的销售额一定就大于分店2的销售额,因为“这样一种看似存在的大于关系实质上是偶然造成的而并不是一种必然”。
黄老板最终决定,使用方差验检查这两个数据。最后,黄老板发现,方差检验的 p 值= 0.2027,那也就意味着,虽然分部1的年平均销售额26.63大于分部2的销售额25.18,但是实质上,两家超市的销售额并没有明显的差异。
说道这里,可能会有一些疑问,没关系,笔者一一自问自答。
如上文所述的一样,“无假设,不检验”,黄老板做了什么样的假设(Hypothesis)?
由于黄老板想要知道两家超市的销售额是否有存在明显的差异 ,所以他的假设就是“样本集1和样本集2不存在显著性差异,换言之这两个集合没有任何区别(销售额间没有区别)!”这就是黄老板的假设。p值怎么回事?
这里并不用管p值是怎样得到的,直接给出结论。在显著性水平α =0.05的情况下,p>0.05接受原假设,p值<0.05拒绝原假设。我们的原假设是样本集Z和样本集H间不存在显著性差异,但是由于p=0.2027>0.05,所以接受原假设,即样本集1和样本集2间不存在显著性差异。当然有接受就有拒接,如果这里的p值小于0.05,那么就要拒绝原假设,即集合1和集合2间存在显著性差异。
怎么做显著性检验?
前面所述都是显著性检验的理论知识,现在开始实践操作(基于MATLAB,主要讲解单因素方差分析)。
假定现在有三组数据:
组一(group1):82 86 79 83 84 85 86 87
组二(group2):74 82 78 75 76 77
组三(group3):79 79 77 78 82 79
现在需要对这三组数据做方差检验,使用anova1函数的方法如下
1.首先将所有的数据放在同一个数组strength中:
>> strength = [82 86 79 83 84 85 86 87 74 82 78 75 76 77 79 79 77 78 82 79];2.设置对应与strength对应位置的标签为alloy:
>> alloy = {'group1','group1','group1','group1','group1','group1','group1','group1','group2','group2','group2','group2','group2','group2','group3','group3','group3','group3','group3','group3'};3.调用anova1函数
>> p = anova1(strength,alloy)最终得到的结果会是一个数值和两幅图。p 值为1.5267e-004,显然,从 p 值看,三组之间存在显著性差异。有一点必须提一下:这里p存在显著性差异并不意味着三组之间两两都存在显著性差异,而只是说明显著性差异在这三组之间存在。
第一幅图是一张表,这张表被称之为 ANOVA 表。如下图所示:
对ANOVA表做详细解析:
Source 表示方差来源(谁的方差),这里的方差来源包括 Groups(组间),Error(组内),Total(总计);
SS(Sum of squares)表示平方和;
df(Degree of freedom)表示自由度;
MS(Mean squares)表示均方差;
F表示F值(F统计量),F值等于组间均方和组内均方的比值,它反映的是随机误差作用的大小;
Prob>F表示p值。
率先普及一下p值和F值之间的关系:
F实际值> F查表值,则 p<=0.05;
F实际值< F查表值,则 p>0.05;
不难看出F值在本例中等于15.4,它正是组间方差92.4和组内方差6的比值。(F分布表可自行查阅,这里不展示了)
根据 n=19( Total 的df),m=2(Groups的df)
可得F0.05( m, n-m-1) = F_0.05( 2, 16) = 3.634。F实际值15.4>F查表值3.634,所以可以判定显著性差异存在,且p值小于0.05。
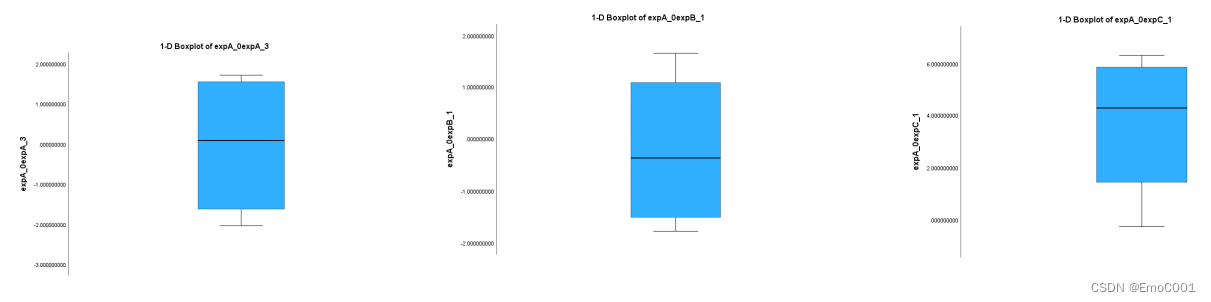
以上讲述了如何仅仅使用F值判断显著性差异的方法并讲述了F值同p值之间的关系。下面这张表格是箱型图,它的看法如下图所表注:
这里有必要提一下 anova1 函数中的参数displayopt 的作用。在大规模的 anova1 调用中(例如把 anova1 放在 for 循环中反复调用),需要把 displayopt 设置为’off’,否则 anova1 每调用一次就会绘制两幅图,这样会迅速的耗费计算机的内存,容易造成程序崩溃。
在上文中,我们提到过。方差分析必须满足两条假设,分别是正态性假定和方差齐性假定。因此,在一个完整的统计工程中,必须首先检测数据的正态性假定和方差齐性假定,这就涉及到另外两个函数 lillietest 正态检验函数(这正是我们上文提到的分布假设检验而不是参数检验,它检验的目标是数据集服从何种分布)和 vartestn 方差齐性检验(这正是我们上文提到的参数检验而不是分布假设检验 ,它检测的目标是数据集的分布服从什么样的参数,这里就是方差)。
函数 lillietest(X)
>> [h,p] = lillietest (strength(1:8))
h =0
p =0.5000解释:h = 0可以认为数据服从正态分布,h=1则认为不服从正态分布
p >0.05可以认为接受原假设h = 0,则数据服从正态分布
>> [h,p] = lillietest (strength(9:14))
h =0
p =0.5000
>> [h,p] = lillietest (strength(15:20))
h =0
p =0.5000可以得出结论,strength中三组数都服从正态分布。
函数:vartestn(X, Group)
>> p = vartestn(strength',alloy','off')p =0.5142p>0.05则说明X中的不同Group是齐次的,也就是方差性齐。
注意:X和Group必须是列向量,否则会报错!!
本文主要讲了单因素方差分析,更多的还有多因素方差分析以及非参数检验等相关知识会在后续博文中介绍。