概率论与数理统计复习总结,仅供笔者复习使用,参考教材:
- 《概率论与数理统计》/ 荣腾中主编. — 第 2 版. 高等教育出版社
- 《2024高途考研数学——概率基础精讲》王喆
概率论与数理统计实际上是两个互补的分支:概率论 在 已知随机变量及其概率分布 的基础上去描述随机现象的统计规律、挖掘随机变量的数字特征与数学性质、计算随机事件的发生概率;数理统计 则是通过随机现象来研究其统计规律性,即通过收集、整理和分析随机变量的观测数据,对随机变量的性质和特征做出合理的推断或预测。
本文主要内容为:数理统计2;
概率论 部分见 概率论与数理统计复习总结1;
数理统计1 部分见 概率论与数理统计复习总结2;
数理统计2 部分见 概率论与数理统计复习总结3;
目录
- 八. 假设检验
- 1. 假设检验的基本原理
- 2. 假设检验的步骤
- 3. 假设检验的两类错误
- 4. 参数假设检验
- 4.1 单个正态总体的参数假设检验
八. 假设检验
假设检验利用样本信息对总体的某种假设进行检验,用于推断数据样本中的差异是否真实存在或是由于随机变异导致的。假设检验一般分为参数假设检验与非参数假设检验,本节主要介绍参数假设检验,即对总体分布中未知参数的假设检验。
1. 假设检验的基本原理
假设检验的基本原理是通过样本数据来对总体特征提出的假设进行推断,通过比较观察到的样本统计量(例如平均值、比例、方差等)与假设中的理论预期值,来判断样本数据是否支持或反对该假设。这样的假设叫做原假设或零假设。
- 原假设:也叫零假设,记为 H 0 H_0 H0。原假设是关于总体特征的默认假设,通常表述为无效、无差异或无影响的假设,如 μ = 8000 \mu=8000 μ=8000、 μ 1 = μ 2 \mu_1=\mu_2 μ1=μ2 等;
- 备择假设:记为 H 1 H_1 H1。备择假设一般是我们希望支持的假设,它表述了我们认为有足够证据支持的观点或猜测。在假设检验中,我们试图通过数据证明备择假设成立,从而拒绝原假设。备择假设可以是双侧的(two-tailed),表明总体特征与原假设有明显差异;也可以是单侧的(one-tailed),表明总体特征在某个方向上显著大于或小于原假设。如 μ ≠ 8000 \mu \neq 8000 μ=8000、 μ 1 ≠ μ 2 \mu_1 \neq \mu_2 μ1=μ2 等;
- 显著性水平:假设检验中事先设定的一个临界值,通常用符号 α \alpha α 表示,用于判断在样本数据中观察到的统计显著性,决定了在假设检验中拒绝原假设的标准,一般取 0.05 或 0.01;
- 拒绝域:样本数据的一个子集,记为 X 0 \mathscr{X}_0 X0。当样本数据落入这个区域时,我们将拒绝原假设,因为拒绝域包含的样本数据在原假设成立的情况下发生的概率较小,我们认为这样的结果对原假设提供了足够的反对证据,从而拒绝原假设。通常,拒绝域的边界由显著性水平 α \alpha α 确定;
- 接受域:样本数据的另一个子集,也是拒绝域的补集,记为 X 0 ‾ \overline{\mathscr{X}_0} X0。当样本数据落入这个区域时,我们将接受原假设,因为接受域包含的样本数据在原假设成立的情况下发生的概率较大,我们认为这样的结果并不足以提供充分证据来拒绝原假设;
2. 假设检验的步骤
- 提出统计假设:明确原假设和备择假设;
- 选择检验统计量:对原假设 H 0 H_0 H0 通过 检验统计量 W = W ( X 1 , X 2 ⋯ , X n ) W=W\left(X_1, X_2 \cdots, X_n\right) W=W(X1,X2⋯,Xn) 的判断需要确定 H 0 H_0 H0 成立条件下统计量 W W W 的精确分布或极限分布,以便能根据显著性水平 α \alpha α 确定 H 0 H_0 H0 的拒绝域;
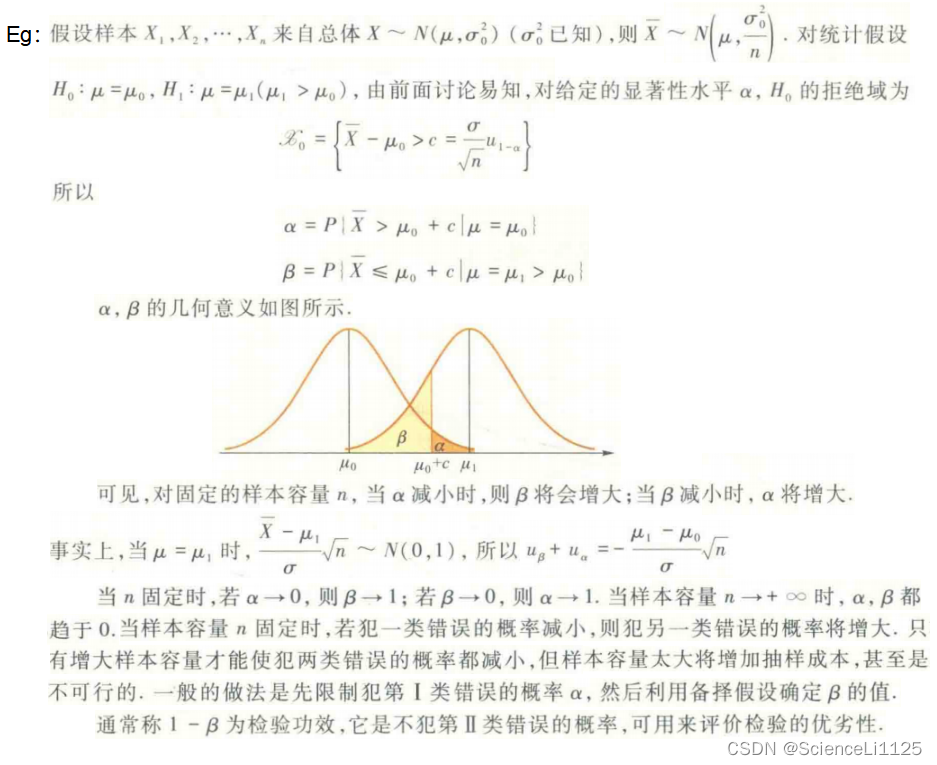
一般地,针对正态总体 N ( μ , σ 2 ) N\left(\mu, \sigma^2\right) N(μ,σ2) 的参数 μ \mu μ 提出假设 H 0 : μ = μ 0 H_0: \mu=\mu_0 H0:μ=μ0,则选择统计量 U = X ˉ − μ 0 σ n ( σ 2 U=\frac{\bar{X}-\mu_0}{\sigma} \sqrt{n}\left(\sigma^2\right. U=σXˉ−μ0n(σ2 已知) 或 T = X ˉ − μ 0 S n T=\frac{\bar{X}-\mu_0}{S} \sqrt{n} T=SXˉ−μ0n ( σ 2 \sigma^2 σ2 末知);针对正态总体 N ( μ , σ 2 ) N\left(\mu, \sigma^2\right) N(μ,σ2) 的参数 σ 2 \sigma^2 σ2 提出假设 H 0 : σ 2 = σ 0 2 H_0: \sigma^2=\sigma_0^2 H0:σ2=σ02,则选择统计量 χ 2 = ( n − 1 ) S 2 σ 0 2 \chi^2=\frac{(n-1) S^2}{\sigma_0^2} χ2=σ02(n−1)S2;针对总体 B ( 1 , p ) B(1, p) B(1,p) 的参数 p p p 提出假设 H 0 : p = p 0 H_0: p=p_0 H0:p=p0,则选择统计量 U = X ˉ − p 0 p 0 ( 1 − p 0 ) n U=\frac{\bar{X}-p_0}{\sqrt{p_0\left(1-p_0\right)}} \sqrt{n} U=p0(1−p0)Xˉ−p0n 等。通常检验方法由统计量的分布来命名,如 U U U 检验法、 t t t 检验法、 χ 2 \chi^2 χ2 检验法、 F F F 检验法等。
- 确立拒绝域形式和拒绝域:通过备择假设 H 1 H_1 H1 来确立拒绝域的形式。由显著性水平 α \alpha α,拒绝域 X 0 \mathscr{X}_0 X0 的形式,检验统计量及分布和 P { ( X 1 , X 2 , ⋯ , X n ) ∈ X 0 ∣ H 0 成立 } ⩽ α P\left\{\left(X_1, X_2, \cdots, X_n\right) \in \mathscr{X}_0 \mid H_0 \text { 成立 } \right\} \leqslant \alpha P{(X1,X2,⋯,Xn)∈X0∣H0 成立 }⩽α 可确定待定常数 c c c,这就确定了拒绝域 X 0 \mathscr{X}_0 X0,通常 α \alpha α 选取 0.01,0.05 或 0.10;
一般地,如果 H 1 : μ ≠ μ 0 H_1: \mu \neq \mu_0 H1:μ=μ0 表示总体均值 μ \mu μ 与 μ 0 \mu_0 μ0 有显著差异,用 X ˉ \bar{X} Xˉ 去估计参数 μ \mu μ 和引人待定常数 c c c 预估差异大小,即小概率事件为 { X ˉ − μ 0 < − c } ∪ { X ˉ − μ 0 > \left\{\bar{X}-\mu_0<-c\right\} \cup\left\{\bar{X}-\mu_0>\right. {Xˉ−μ0<−c}∪{Xˉ−μ0> c } c\} c},那么拒绝域形式为 { ∣ X ˉ − μ 0 ∣ > c } \left\{\left|\bar{X}-\mu_0\right|>c\right\} { Xˉ−μ0 >c},称 H 1 : μ ≠ μ 0 H_1: \mu \neq \mu_0 H1:μ=μ0 为双侧假设检验问题;如果 H 1 : μ > μ 0 H_1: \mu>\mu_0 H1:μ>μ0,则选择拒绝域 { X ˉ − μ 0 > c } \left\{\bar{X}-\mu_0>c\right\} {Xˉ−μ0>c},称 H 1 : μ > μ 0 H_1: \mu>\mu_0 H1:μ>μ0 为单侧假设检验问题。
- 作出判断或决策:根据抽样信息,计算检验统计量的样本值 w = W ( x 1 , x 2 , ⋯ , x n ) w=W\left(x_1, x_2, \cdots, x_n\right) w=W(x1,x2,⋯,xn)。若 ( x 1 \left(x_1\right. (x1, x 2 , ⋯ , x n ) ∈ X 0 \left.x_2, \cdots, x_n\right) \in \mathscr{X}_0 x2,⋯,xn)∈X0,则拒绝 H 0 H_0 H0,接受 H 1 H_1 H1;否则接受 H 0 H_0 H0;
3. 假设检验的两类错误
由于抽样的随机性和小概率原理,假设检验所作出的判断可能与事实不符合,出现推断错误。把拒绝 H 0 H_0 H0 可能犯的错误称为第Ⅰ类错误或弃真错误;把接受 H 0 H_0 H0 的判断可能犯的错误称为第Ⅱ类错误或纳伪错误。
| \真实情况 假设检验结果\ | H 0 H_0 H0 成立 | H 0 H_0 H0 不成立 |
|---|---|---|
| 拒绝 H 0 H_0 H0 | 犯第Ⅰ类错误(弃真错误) | 推断正确 |
| 接受 H 0 H_0 H0 | 推断正确 | 犯第Ⅱ类错误(纳伪错误) |
- 第Ⅰ类错误:原假设 H 0 H_0 H0 为真,由于样本的随机性,使样本观测值落入拒绝域 X 0 \mathscr{X}_0 X0 中,判断为拒绝 H 0 H_0 H0。错误的概率记为 α \alpha α:
α = P { 拒绝 H 0 ∣ H 0 成立 } = P { ( X 1 , X 2 , ⋯ , X n ) ∈ X 0 ∣ H 0 成立 } \alpha = P\{拒绝 H_0 | H_0 成立\} = P\left\{\left(X_1, X_2, \cdots, X_n\right) \in \mathscr{X}_0 \mid H_0 成立 \right\} α=P{拒绝H0∣H0成立}=P{(X1,X2,⋯,Xn)∈X0∣H0成立} - 第Ⅱ类错误:原假设 H 0 H_0 H0 为假,判断为接受 H 0 H_0 H0;错误的概率记为 β \beta β:
β = P { 接受 H 0 ∣ H 0 不成立 } = P { ( X 1 , X 2 , ⋯ , X n ) ∈ X 0 ‾ ∣ H 0 不成立 } \beta = P\{接受 H_0 | H_0 不成立\} = P\left\{\left(X_1, X_2, \cdots, X_n\right) \in \overline{\mathscr{X}_0} \mid H_0 不成立 \right\} β=P{接受H0∣H0不成立}=P{(X1,X2,⋯,Xn)∈X0∣H0不成立}
在样本容量固定的条件下,减少犯一类错误的概率,就会增加犯另一类错误的概率。举例如下:
4. 参数假设检验
实际问题中很多随机变量服从或近似服从正态分布,因此这节重点介绍单个正态总体的参数假设检验。
4.1 单个正态总体的参数假设检验
-
参数 μ \mu μ 的假设检验:

-
参数 σ 2 \sigma^2 σ2 的假设检验( μ \mu μ 未知):

拒绝域同时在数轴左右两侧的假设检验称为 双侧假设检验 或双尾假设检验,拒绝域在数轴左侧或右侧的假设检验分别称为左侧假设检验或右侧假设检验,统称为 单侧检验 或单尾检验。双侧假设检验关注的是 总体参数是否有明显的变化,而单侧假设检验关注 总体参数明显变化的方向,左侧检验关注总体参数是否明显减少,右侧检验关注总体参数是否明显增加。举例如下: