概述

字符串匹配（查找）是字符串的一种基本操作：给定带匹配查询的文本串S和目标子串T，T也叫做模式串。在文本S中找到一个和模式T相符的子字符串，并返回该子字符串在文本中的位置。

暴力匹配

Brute Force Algorithm，也叫朴素字符串匹配算法，Naive String Matching Algorithm。
基本思路就是将字符一个一个地进行比较：

• 如果S和T两个字符串的第一个字符相同就比较第二个字符,如果相同就一直继续；
• 如果其中有某一个字符不同，则将T字符串向后移一位，将S字符串的第二个字符与T的字符串的第一个字符重新开始比较。
• 循环往复，一直到结束

实现

public static int bf(String text, String pattern) {int m = text.length();int n = pattern.length();for (int i = 0; i <= m - n; i++) {boolean flag = true;for (int j = 0; j < n; j++) {if (text.charAt(i + j) != pattern.charAt(j)) {flag = false;break;}}if (flag) {return i;}}return -1;
}

KMP

D.E.Knuth，J.H.Morris 和 V.R.Pratt发明，一种字符串匹配的改进算法，利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。KMP算法只需要对文本串搜索一次，时间复杂度是O(n)。

KMP 算法的关键是求 next 数组。next 数组的长度为模式串的长度。next 数组中每个值代表模式串中当前字符前面的字符串中，有多大长度的相同前缀后缀。

原理

暴力匹配
给定字符串A和B，判断B是否是A的子串。暴力匹配的方法：从A的第一个字符开始，比较A的第一个字符和B的第一个字符是否相同，相同则比较A的第二个字符和B的第二个字符，不相同，则从A的第二个字符开始，与B的第一个字符开始比较。以此类推。相当于一步步右移B的动作。

暴力匹配，效率低，体现在一步步移动，尤其是在B的前n-1个字符都能匹配成功，最后一个字符匹配失败，或B子串较长的情况下。KMP利用匹配表的概念来优化匹配效率。

匹配表
对于给定的字符串B，如abcab：

• 前缀：除了最后个字符外，所有的顺序组合方式：a、ab、abc、abca
• 后缀：除了第一个字符外，所有的顺序组合方式：bcab、cab、ab、b

匹配值，对子串的每个字符组合寻找出前缀和后缀，比较是否有相同的，相同的字符组合有几位，匹配值就是几。

比如针对给定的字符串abcab，其匹配值字符串为00012：

• a，无前后缀，匹配值=0
• ab，前缀{a}，后缀{b}，无共同字符，匹配值=0
• abc，前缀{a}{ab}，后缀{c}{bc}，无共同字符，匹配值=0
• abca，前缀{a}{ab}{abc}，后缀{a}{ca}{bca}，共同字符{a}，匹配值=1
• abcab，前缀{a}{ab}{abc}{abca}，后缀{b}{ab}{cab}{bcab}，共同字符{ab}，匹配值=2

基于匹配表，不需要一个个移动，移动步数 = 成功匹配的位数 - 匹配表里面的匹配值。

实现

给出一个KMP算法实现：

/*** 利用KMP算法求解pattern是否在text中出现过** @param text    文本串* @param pattern 模式串* @return pattern在text中出现，则返回true，否则返回false*/
public static boolean kmpSearch(String text, String pattern) {// 部分匹配数组int[] partMatchTable = kmpNext(pattern);// text中的指针int i = 0;// pattern中的指针int j = 0;while (i < text.length()) {if (text.charAt(i) == pattern.charAt(j)) {// 字符匹配，则两个指针同时后移i++;j++;} else if (j > 0) {// 字符失配，则利用next数组，移动j指针，避免i指针回退j = partMatchTable[j - 1];} else {// pattern中的第一个字符就失配i++;}if (j == pattern.length()) {// 搜索成功return true;}}return false;
}private static int[] kmpNext(String pattern) {int[] next = new int[pattern.length()];next[0] = 0;int j=0;for (int i = 1; i < pattern.length(); i++) {while (j > 0 && pattern.charAt(i) != pattern.charAt(j)){//前后缀相同j = next[j - 1];}if (pattern.charAt(i) == pattern.charAt(j)){//前后缀不相同j++;}next[i] = j;}return next;
}

Boyer-Moore

Boyer-Moore 算法在实际应用中比 KMP 算法效率高，据说各种文本编辑器的查找功能，包括Linux 里的 grep 命令，都是采用 Boyer-Moore 算法。该算法有坏字符和好后缀两个概念，字符串从后往前匹配。 一般情况下，比KMP算法快3-5倍。

原理

假设文本串S长度为n，模式串T长度为m，BM算法的主要特征为：

• 从右往左进行比较匹配（一般的字符串搜索算法如KMP都是从左往右进行匹配）；
• 算法分为两个阶段：预处理阶段和搜索阶段；
• 预处理阶段时间和空间复杂度都是是O(m+)，是字符集大小，一般为256；
• 搜索阶段时间复杂度是O(mn)；
• 当模式串是非周期性的，在最坏的情况下算法需要进行3n次字符比较操作；
• 算法在最好的情况下达到O(n/m)，即只需要n/m次比较。

而BM算法在移动模式串的时候是从左到右，而进行比较的时候是从右到左的。

BM算法的精华就在于BM(text, pattern)，BM算法当不匹配的时候一次性可以跳过不止一个字符。即它不需要对被搜索的字符串中的字符进行逐一比较，而会跳过其中某些部分。通常搜索关键字越长，算法速度越快。它的效率来自于这样的事实：对于每一次失败的匹配尝试，算法都能够使用这些信息来排除尽可能多的无法匹配的位置。即它充分利用待搜索字符串的一些特征，加快搜索的步骤。

BM算法包含两个并行的算法（也就是两个启发策略）：坏字符算法（bad-character shift）和好后缀算法（good-suffix shift）。这两种算法的目的就是让模式串每次向右移动尽可能大的距离（即BM()尽可能大）。

实现

/*** Boyer-Moore算法是一种基于后缀匹配的模式串匹配算法，后缀匹配就是模式串从右到左开始比较，但模式串的移动还是从左到右的。* 字符串匹配的关键就是模式串的如何移动才是最高效的，Boyer-Moore为了做到这点定义了两个规则：坏字符规则和好后缀规则<br>* 坏字符规则<bR>* 1.如果坏字符没有出现在模式字符中，则直接将模式串移动到坏字符的下一个字符：<br>* 2.如果坏字符出现在模式串中，则将模式串最靠近好后缀的坏字符（当然这个实现就有点繁琐）与母串的坏字符对齐：<br>* 好后缀规则<bR>* 1.模式串中有子串匹配上好后缀，此时移动模式串，让该子串和好后缀对齐即可，如果超过一个子串匹配上好后缀，则选择最靠靠近好后缀的子串对齐。<br>* 2.模式串中没有子串匹配上后后缀，此时需要寻找模式串的一个最长前缀，并让该前缀等于好后缀的后缀，寻找到该前缀后，让该前缀和好后缀对齐即可。<br>* 3.模式串中没有子串匹配上后后缀，并且在模式串中找不到最长前缀，让该前缀等于好后缀的后缀。此时，直接移动模式到好后缀的下一个字符。<br>*/
public static List<Integer> bmMatch(String text, String pattern) {List<Integer> matches = new ArrayList<>();int m = text.length();int n = pattern.length();// 生成模式字符串的坏字符移动结果Map<Character, Integer> rightMostIndexes = preprocessForBadCharacterShift(pattern);// 匹配的节点位置int alignedAt = 0;// 如果当前节点在可匹配范围内，即当前的A[k]必须在A[0, m-n-1)之间，否则没有必要做匹配while (alignedAt + (n - 1) < m) {// 循环模式组，查询模式组是否匹配 从模式串的最后面开始匹配，并逐渐往前匹配for (int indexInPattern = n - 1; indexInPattern >= 0; indexInPattern--) {// 1 定义待查询字符串中的当前匹配位置.int indexInText = alignedAt + indexInPattern;// 2 验证带查询字符串的当前位置是否已经超过最长字符，如果超过，则表示未查询到.if (indexInText >= m) {break;}// 3 获取到带查询字符串和模式字符串中对应的待匹配字符char x = text.charAt(indexInText);char y = pattern.charAt(indexInPattern);// 4 验证结果if (x != y) {// 4.1 如果两个字符串不相等，则寻找最坏字符串的结果，生成下次移动的队列位置Integer r = rightMostIndexes.get(x);if (r == null) {alignedAt = indexInText + 1;} else {// 当前坏字符串在模式串中存在，则将模式串最靠近好后缀的坏字符与母串的坏字符对齐，shift 实际为模式串总长度int shift = indexInText - (alignedAt + r);alignedAt += shift > 0 ? shift : 1;}// 退出匹配break;} else if (indexInPattern == 0) {// 4.2 匹配到的话 并且最终匹配到模式串第一个字符，便是已经找到匹配串，记录下当前的位置matches.add(alignedAt);alignedAt++;}}}return matches;
}/*** 坏字符串* 依据待匹配的模式字符串生成一个坏字符串的移动列，该移动列中表明当一个坏字符串出现时，需要移动的位数*/
private static Map<Character, Integer> preprocessForBadCharacterShift(String pattern) {Map<Character, Integer> map = new HashMap<>();for (int i = pattern.length() - 1; i >= 0; i--) {char c = pattern.charAt(i);if (!map.containsKey(c)) {map.put(c, i);}}return map;
}

参考：百度百科

Sunday

Daniel M.Sunday 于 1990 年提出的字符串模式匹配算法。其效率在匹配随机的字符串时比其他匹配算法更快。平均时间复杂度为O(n)，最差情况的时间复杂度为O(n*m)。

原理

Sunday 算法跟 KMP 算法一样，是从前往后匹配。在匹配失败时，关注文本串中参加匹配的最末位字符的下一位字符，如果该字符不在模式串中，则整个模式串移动到该字符之后。如果该字符在模式串中，将模式串右移使对应的字符对齐。

Sunday算法和BM算法稍有不同的是，Sunday算法是从前往后匹配，在匹配失败时关注的是主串中参加匹配的最末位字符的下一位字符。

• 如果该字符没有在模式串中出现则直接跳过，即移动位数 = 模式串长度 + 1；
• 否则，其移动位数 = 模式串长度 - 该字符最右出现的位置(以0开始) = 模式串中该字符最右出现的位置到尾部的距离 + 1。

举例说明Sunday算法。假定现在要在主串substring searching中查找模式串search：

• 刚开始时，把模式串与文主串左边对齐：
  
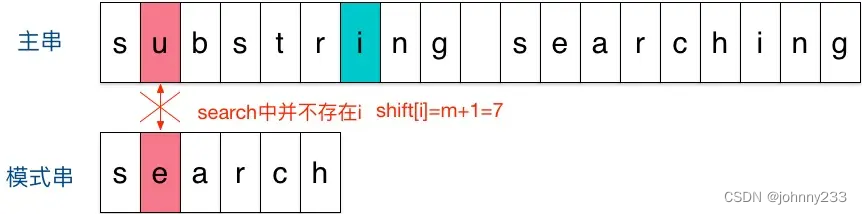
• 结果发现在第2个字符处发现不匹配，不匹配时关注主串中参加匹配的最末位字符的下一位字符，即标粗的字符i，模式串search中并不存在i，模式串直接跳过一大片，向右移动位数 = 匹配串长度 + 1 = 6 + 1 = 7，从 i 之后的那个字符（即字符n）开始下一步的匹配：
  
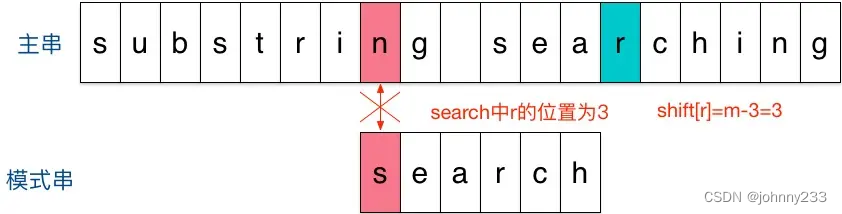
• 结果第一个字符就不匹配，再看主串中参加匹配的最末位字符的下一位字符r，它出现在模式串中的倒数第3位，于是把模式串向右移动3位（m - 3 = 6 - 3 = r 到模式串末尾的距离 + 1 = 2 + 1 =3），使两个r对齐：
  
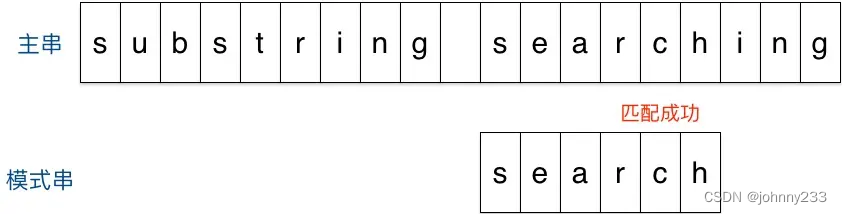
• 匹配成功。

Sunday算法的缺点：算法核心依赖于move数组，而move数组的值则取决于模式串，那么就可能存在模式串构造出很差的move数组。

实现

/*** sunday 算法** @param text    文本串* @param pattern 模式串* @return 匹配失败返回-1，匹配成功返回文本串的索引(从0开始)*/
public static int sunday(char[] text, char[] pattern) {int tSize = text.length;int pSize = pattern.length;int[] move = new int[ASCII_SIZE];// 主串参与匹配最末位字符移动到该位需要移动的位数for (int i = 0; i < ASCII_SIZE; i++) {move[i] = pSize + 1;}for (int i = 0; i < pSize; i++) {move[pattern[i]] = pSize - i;}// 模式串头部在字符串位置int s = 0;// 模式串已经匹配的长度int j;// 到达末尾之前while (s <= tSize - pSize) {j = 0;while (text[s + j] == pattern[j]) {j++;if (j >= pSize) {return s;}}s += move[text[s + pSize]];}return -1;
}

对比

仅做示例用，不同的算法在不同情况下表现不一致。与待搜索的字符串文本和模式匹配字符串有关。

public static void main(String[] args) {String text = "abcagfacjkackeac";String pattern = "ackeac";Stopwatch stopwatch = Stopwatch.createStarted();int bfRes = bf(text, pattern);stopwatch.stop();log.info("bf result:{}, take {}ns", bfRes, stopwatch.elapsed(TimeUnit.NANOSECONDS));stopwatch.reset();stopwatch.start();boolean kmpRes = kmpSearch(text, pattern);stopwatch.stop();log.info("kmp result:{}, take {}ns", kmpRes, stopwatch.elapsed(TimeUnit.NANOSECONDS));stopwatch.reset();stopwatch.start();List<Integer> bmMatch = bmMatch(text, pattern);stopwatch.stop();log.info("bmMatch result:{}, take {}ns", bmMatch, stopwatch.elapsed(TimeUnit.NANOSECONDS));stopwatch.reset();stopwatch.start();int sunday = sunday(text.toCharArray(), pattern.toCharArray());stopwatch.stop();log.info("sunday result:{}, take {}ns", sunday, stopwatch.elapsed(TimeUnit.NANOSECONDS));
}

某次输出结果：

bf result:10, take 8833ns
kmp result:true, take 4541ns
bmMatch result:[10], take 90500ns
sunday result:10, take 5458ns

测试结果仅供参考。

参考

• 动画解释KMP算法