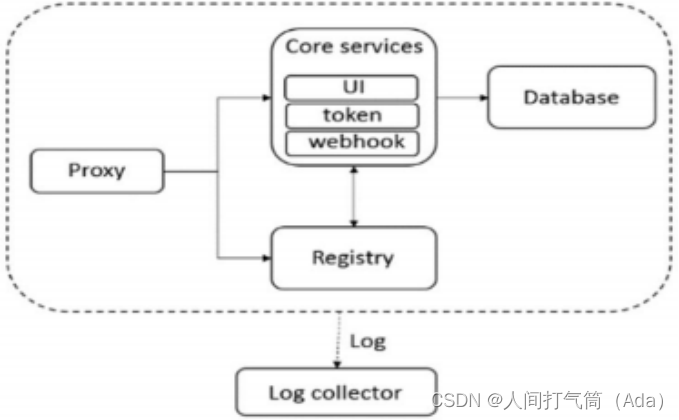
序号	内容
1	【数理知识】自由度 degree of freedom 及自由度的计算方法
2	【数理知识】刚体 rigid body 及刚体的运动
3	【数理知识】刚体基本运动，平动，转动
4	【数理知识】向量数乘，内积，外积，matlab代码实现
5	【数理知识】协方差，随机变量的的协方差，随机变量分别是单个数字和向量时的协方差
6	【数理知识】已知 N>=3 个点在前后时刻的坐标，求刚体平移矩阵，旋转矩阵，且这 N>=3 点间距离始终不变代表一个刚体

协方差是统计学中一个重要的概念，它用于衡量两个随机变量的总体误差。简单来说，协方差用于度量两个变量之间的线性关系。

如果协方差是正的，那么两个变量可能会同时增大或减小，这表明它们之间可能存在正相关的关系。
如果协方差是负的，那么其中一个变量增大时，另一个可能减小，这表明它们之间可能存在负相关的关系。
如果协方差是 $0$，那么两个变量可能不相关。

协方差的一个主要应用是在统计和概率理论中，用于衡量两个随机变量的联动性。此外，协方差矩阵在多元统计分析、信号处理、控制系统、投资组合优化等多个领域都有广泛的应用。

然而，协方差有一个缺点，就是它的值受到变量尺度的影响。例如，如果你测量同一个物理量，但是使用的单位不同（比如使用米和厘米），你会得到完全不同的协方差。为了克服这个问题，我们经常使用相关系数（协方差除以两个变量的标准差），这是一个标准化的协方差，不受尺度的影响，范围在-1到1之间。

1. 计算协方差

总的来说，计算协方差可以使用两种方式。区别在于是否知道全部的数据量，也就是说我们是知道随机变量的期望均值，还是仅知道样本数据的样本均值。至于期望均值和样本均值的区别，请查阅文章：【LinearAlgebra】12.1 Mean, Variance, and Probability。

---

第一种，当我们知道所有的数据（总数据量为 $N$）时，也就是知道了具体的期望值，可以使用公式

$$\begin{array}{rl}\text{Cov}(X,Y)& =\text{E}[(X-\mu X)(Y-\mu Y)]\end{array}$$

来计算。其中 $\mu X、\mu Y$ 分别是 $X$ 和 $Y$ 的期望值。

---

第二种是仅知道样本数据（样本数量为 $n$，总数据量为 $N$）时，可以使用公式

$$\begin{array}{rl}\text{Cov}(X,Y)& =\frac{{\sum }_i^n(x_i-\bar{x})(y_i-\bar{y})}{n-1}\end{array}$$

来估算（注意不是计算）协方差。其中 $x_i、y_i$ 是两个随机变量已知的样本数据，$\bar{x}、\bar{y}$ 是两个随机变量的平均值。注意这里是除以（$n-1$）而不是 $n$，因为这是无偏估计，当样本数据用来估计总计参数时，需要这样处理。

---

接下来用同一组数据，分别使用两种方式来计算协方差，看下效果。

---

1. 计算方式一：使用期望值

假设有两个随机变量 X = { 1 , 2 , 2 , 2 , 3 } X = \{1, 2, 2, 2, 3\} X={1,2,2,2,3}， Y = { 6 , 6 , 7 , 7 , 8 } Y = \{6, 6, 7, 7, 8\} Y={6,6,7,7,8}。我们能够分别计算二者的期望均值为
$$\begin{array}{rl}\mu X& =(1+2+2+2+3)/5=2\\ \mu Y& =(6+6+7+7+8)/5=6.8\end{array}$$

那么协方差为

$$\begin{array}{rl}\text{Cov}(X,Y)& =\text{E}[(X-\mu X)(Y-\mu Y)]\\ & =[(1-2)(6-6.8)+(2-2)(6-6.8)+(2-2)(7-6.8)+(2-2)(7-6.8)+(3-2)(8-6.8)]/5\\ & =[0.8+0+0+0+1.2]/5\\ & =0.4\end{array}$$

所以，这两个随机变量的协方差为 $0.4$。

---

2. 计算方式二：使用样本数据

还是上边的两个随机变量。但假如我们仅知道其中的 $3$ 个，如 X = { 1 , 2 , 2 , 3 } X = \{1, 2, 2, 3\} X={1,2,2,3}， Y = { 6 , 6 , 7 , 8 } Y = \{6, 6, 7, 8\} Y={6,6,7,8}，同时也不知道每个样本的概率。这时候，我们仅能计算出来样本均值，也就是

$$\begin{array}{rl}\bar{x}& =(1+2+2+3)/4=2\\ \bar{y}& =(6+6+7+8)/4=6.75\end{array}$$

那么协方差为

$$\begin{array}{rl}\text{Cov}(X,Y)& =\frac{{\sum }_i^n(x_i-\bar{x})(y_i-\bar{y})}{n-1}\\ & =[(1-2)(6-6.75)+(2-2)(6-6.75)+(2-2)(7-6.75)+(3-2)(8-6.75)]/(4-1)\\ & =[0.75+0+0+1.25]/3\\ & =0.6667\end{array}$$

所以，用这一组样本估算出来的协方差为 $0.6667$。

---

在上述样本的基础上，假如我们知道了其概率，也就是样本为 X = { 1 , 2 , 2 , 3 } X = \{1, 2, 2, 3\} X={1,2,2,3}， Y = { 6 , 6 , 7 , 8 } Y = \{6, 6, 7, 8\} Y={6,6,7,8}，同时每个样本的概率为 P = { 0.2 , 0.2 , 0.4 , 0.2 } P = \{0.2, 0.2, 0.4, 0.2\} P={0.2,0.2,0.4,0.2}。那此时就可以计算出来随机变量的期望值为

$$\begin{array}{rl}\mu X& =0.2\ast 1+0.2\ast 2+0.4\ast 2+0.2\ast 3=2\\ \mu Y& =0.2\ast 6+0.2\ast 6+0.4\ast 7+0.2\ast 8=6.8\end{array}$$

计算协方差为

$$\begin{array}{rl}\text{Cov}(X,Y)& =\sum p_i(x_i-\mu X)(y_i-\mu Y)\\ & =0.2\ast (1-2)(6-8)+0.2\ast (2-2)(6-8)+0.4\ast (2-2)(7-8)+0.2\ast (3-2)(8-8)\\ & =0.2\ast (2)+0.2\ast (0)+0.4\ast (0)+0.2\ast (0)\\ & =0.4\end{array}$$

---

3. 对比两种方式

至于为什么知道了样本的概率就能知道精准知道协方差了，可以看一下数据的排列。

首先，全部数据可以排列成

$${\text{Data}}_N=\left[\begin{array}{cccccc}{x}_i& 1& 2& 2& 2& 3\\ y_i& 6& 6& 7& 7& 8\\ p_i& 0.2& 0.2& 0.2& 0.2& 0.2\end{array}\right]=\left[\begin{array}{ccccc}{x}_i& 1& 2& 2& 3\\ y_i& 6& 6& 7& 8\\ p_i& 0.2& 0.2& 0.4& 0.2\end{array}\right]$$

而使用样本估算的方法时，我们用的应该是

$${\text{Data}}_n=\left[\begin{array}{ccccc}{x}_i& 1& 2& 2& 3\\ y_i& 6& 6& 7& 8\\ p_i& 0.25& 0.25& 0.25& 0.25\end{array}\right]$$

所以，对比观看一下可以知道，我们在样本估算时，实际也是假设了每个样本出现的概率都是相同的。

---

2. 随机变量为二维平面的点

在上述描述中，我们随机变量中的样本都是数字，也就是每个样本数据的维度都是 $1$ 维的。接下来假设样本为二维平面中的点，也就是样本数据的维度为 $2$ 维。

假设随机变量的样本为：$X=\{(1,2),(3,4),(5,6)\}$，$Y=\{(2,3),(4,5),(6,7)\}$。首先计算均值为

$$\begin{array}{rl}\bar{x}& =(1+3+5,2+4+6)/3=(3,4)\\ \bar{y}& =(2+4+6,3+5+7)/3=(4,5)\end{array}$$

然后，我们计算协方差矩阵。在这种情况下，协方差矩阵是一个 $2\times 2$ 的矩阵，其每个元素 $\text{Cov}(X,Y{)}_{ij}$ 是 $X$ 的第 $i$ 个维度和 $Y$ 的第 $j$ 个维度的协方差。在这种情况下，我们计算的是 $X$ 和 $Y$ 之间的协方差，而不是 $X$ 和 $Y$ 内部的协方差，所以我们是在计算 $X$ 的第 $i$ 个维度和 $Y$ 的第 $j$ 个维度。

矩阵的每一个元素 $(i,j)$ 都是通过以下公式计算得到的：

$$\begin{array}{rl}\text{Cov}(X,Y{)}_{ij}& =\frac{{\sum }_k^{n=3}(x_{ki}-{\bar{x}}_i)(y_{kj}-{\bar{y}}_i)}{n-1}\end{array}$$

其中 $x_{ki}$ 表示第 $k$ 个样本的第 $i$ 个维度的值，${\bar{x}}_i$ 表示均值的第 $i$ 个维度。

依次代入数值并展开有

$$\begin{array}{rl}\text{Cov}(X,Y{)}_{i=1,j=1}& =\frac{(1-3)(2-4)+(3-3)(4-4)+(5-3)(6-4)}{3-1}=4\\ \text{Cov}(X,Y{)}_{i=1,j=2}& =\frac{(1-3)(3-5)+(3-3)(5-5)+(5-3)(7-5)}{3-1}=4\end{array}$$

$$\begin{array}{rl}\text{Cov}(X,Y{)}_{i=2,j=1}& =\frac{(2-4)(2-4)+(4-4)(4-4)+(6-4)(6-4)}{3-1}=4\\ \text{Cov}(X,Y{)}_{i=2,j=2}& =\frac{(2-4)(3-5)+(4-4)(5-5)+(6-4)(7-5)}{3-1}=4\end{array}$$

故协方差矩阵为

$$\begin{array}{rl}\text{Cov}(X,Y)& =\left[\begin{array}{cc}4& 4\\ 4& 4\end{array}\right]\end{array}$$

---

3. 随机变量为三维空间的点

接下来假设样本为三维空间中的点，也就是样本数据的维度为 $3$ 维。

假设随机变量的样本为：$X=\{(1,2,3),(4,5,6),(7,8,9)\}$，$Y=\{(2,3,4),(5,6,7),(8,9,10)\}$。首先计算均值为

$$\begin{array}{rl}\bar{x}& =(1+4+7,2+5+8,3+6+9)/3=(4,5,6)\\ \bar{y}& =(2+5+8,3+6+9,4+7+10)/3=(5,6,7)\end{array}$$

然后，我们计算协方差矩阵。在这种情况下，协方差矩阵是一个 $3\times 3$ 的矩阵，其每个元素 $\text{Cov}(X,Y{)}_{ij}$ 是 $X$ 的第 $i$ 个维度和 $Y$ 的第 $j$ 个维度的协方差。

矩阵的每一个元素 $(i,j)$ 都是通过以下公式计算得到的：

$$\begin{array}{rl}\text{Cov}(X,Y{)}_{ij}& =\frac{{\sum }_k^{n=3}(x_{ki}-{\bar{x}}_i)(y_{kj}-{\bar{y}}_i)}{n-1}\end{array}$$

依次代入数值并展开有

$$\begin{array}{rl}\text{Cov}(X,Y{)}_{i=1,j=1}& =\frac{(1-4)(2-5)+(4-4)(3-5)+(7-4)(4-5)}{3-1}=3\\ \text{Cov}(X,Y{)}_{i=1,j=2}& =\frac{(1-4)(5-6)+(4-4)(6-6)+(7-4)(7-6)}{3-1}=3\\ \text{Cov}(X,Y{)}_{i=1,j=3}& =\frac{(1-4)(8-7)+(4-4)(9-7)+(7-4)(10-7)}{3-1}=3\end{array}$$

$$\begin{array}{rl}\text{Cov}(X,Y{)}_{i=2,j=1}& =\frac{(2-5)(2-5)+(5-5)(3-5)+(8-5)(4-5)}{3-1}=3\\ \text{Cov}(X,Y{)}_{i=2,j=2}& =\frac{(2-5)(5-6)+(5-5)(6-6)+(8-5)(7-6)}{3-1}=3\\ \text{Cov}(X,Y{)}_{i=2,j=3}& =\frac{(2-5)(8-7)+(5-5)(9-7)+(8-5)(10-7)}{3-1}=3\end{array}$$

$$\begin{array}{rl}\text{Cov}(X,Y{)}_{i=3,j=1}& =\frac{(3-6)(2-5)+(6-6)(3-5)+(9-6)(4-5)}{3-1}=3\\ \text{Cov}(X,Y{)}_{i=3,j=2}& =\frac{(3-6)(5-6)+(6-6)(6-6)+(9-6)(7-6)}{3-1}=3\\ \text{Cov}(X,Y{)}_{i=3,j=3}& =\frac{(3-6)(8-7)+(6-6)(9-7)+(9-6)(10-7)}{3-1}=3\end{array}$$

故协方差矩阵为

$$\begin{array}{rl}\text{Cov}(X,Y)& =\left[\begin{array}{ccc}3& 3& 3\\ 3& 3& 3\\ 3& 3& 3\end{array}\right]\end{array}$$

---

4. 马同学视频例子

如果看公式比较抽象的，也可以看看马同学图解数学中的视频讲解：如何通俗地解释协方差 - bilibili。我截取了几个关键步骤的视频截图。

使用的是身高 $x_i$ 和体重 $y_i$ 这两个指标为例子。

想要知道身高和体重的相关性，可以使用下边这种计算方式。

$$\begin{array}{r}\sum (x_i-\bar{x})(y_i-\bar{y})\end{array}\text{\hspace{1em}(1)}$$

其中 $\bar{x},\bar{y}$ 分别表示身高，体重的平均值。

但数据差异较大时，就会出现错误判断。

这时候引入数据出现的概率 $p_i$，同时替换数字平均值 $\bar{x},\bar{y}$ 为加权平均值 $\mu X,\mu Y$。
此时公式（1）变为

$$\begin{array}{rl}& \sum (x_i-\bar{x})(y_i-\bar{y})\\ & \sum p_i(x_i-\mu X)(y_i-\mu Y)\end{array}\text{\hspace{1em}(2)}$$

其中 $\mu X,\mu Y$ 表示加权平均，$p_i$ 表示每一项的概率。

最后，将式子改写成期望的形式有

$$\begin{array}{rl}& \sum (x_i-\bar{x})(y_i-\bar{y})\\ & \sum p_i(x_i-\mu X)(y_i-\mu Y)\\ \text{Cov}(X,Y)& =\text{E}[(X-\mu X)(Y-\mu Y)]\end{array}\text{\hspace{1em}(3)}$$

---

Ref

1. 如何通俗地解释协方差 - bilibili
2. 从3组对应点中求得最佳的旋转和平移变换