1.数组的概念

2.一维数组的创建和初始化

创建的语句结构

类型  名称 [常量]
int name [99]
char ch[8]
double  score[199]

初始化的语句结构

//完全初始化
int arr[5]={1,2,3,5,9}//不完全初始化
int arr[5]={1} //第一个元素初始化为1，剩下的元素默认为0//错误的初始化
int arr[3]={1,5,9,6}

数组的类型：去掉数组名后留下的额就是数组的类型

3.一维数组的使用

数组的下标：从0开始，n个数组，最后一个的下标是n-1

下标访问操作符：[ ]

int arr[10]={1,2,4,5,7,8,9,6,3,10}
printf("%d",arr[2]);//可以打印arr[2]

4.一维数组在内存中的存储

#include <stdio.h>
int main(){
int arr[5]={1,2,3,4,5}
int i=0;
for(i=0;i<5;i++){
printf("&arr[%d]=%p\n",i,&arr[i]);
}
return 0;%p----打印地址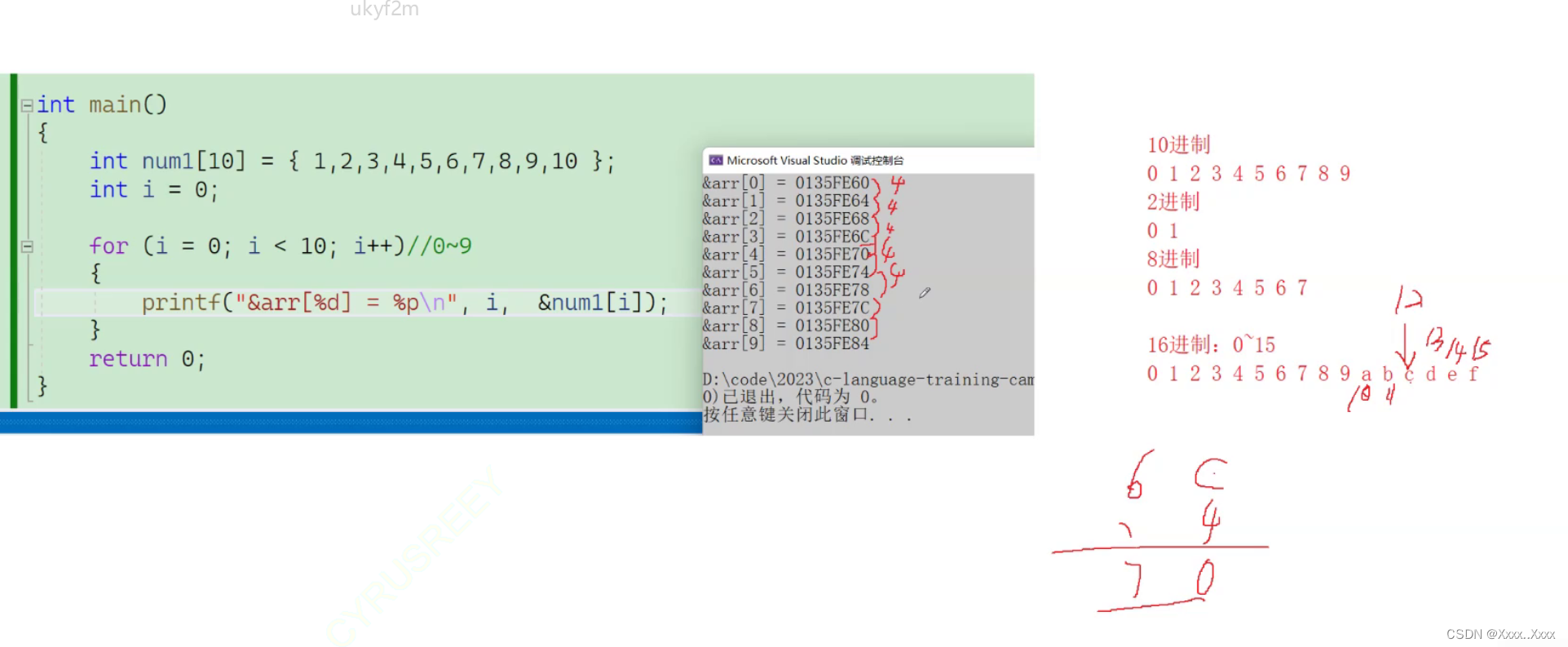

结论数组是连续存放的随着下标的增长，地址是由低到高变化的。相差4是因为int表示的是4个字节。所以每个地址之间相差4个

5.sizeof计算数组元素个数

可以计算元素个数并且遍历到数组的最后一项

6.二维数组的创建

7.二维数组的初始化

8.二维数组的使用

9.二维数组在内存中的存储

10.C99中的变长数组

11.数组练习