1. numpy.matmul() 用法

matmul() 用于计算两个数组的矩阵乘积。示例如下

def matmul_test():array1 = np.array([[[1.0, 3], [1, 1], [2, 3]]])array2 = np.array([[2, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0],[1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0], ])result = np.matmul(array1, array2)print(result)if __name__ == '__main__':matmul_test()

结果输出：

    [[[5. 4. 1. 3. 3. 0. 0. 4. 4. 0. 1. 0.][3. 2. 1. 1. 1. 0. 0. 2. 2. 0. 1. 0.][7. 5. 2. 3. 3. 0. 0. 5. 5. 0. 2. 0.]]]

2. numpy.multiple() 用法

先说说更简单的multiply，如果两个维度完全一样的矩阵用multiply做乘法，那么它们只是进行对应位置元素之间的乘法，得到一个同样维度的矩阵输出。这就是所谓的element-wise product。

def multiple_test():array1 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], ndmin=3)array2 = np.array([[9, 8, 7], [6, 5, 4], [3, 2, 1]], ndmin=3)result = np.multiply(array1, array2)print(result)
if __name__ == '__main__':multiple_test()

结果输出

     [[[ 9 16 21][24 25 24][21 16  9]]]

3. numpy.dot()用法

线性代数中矩阵相乘，被称为点积运算（Dot Product），又称为内积。首先根据线性代数的知识，特别需要注意的一点是：
矩阵X1和矩阵X2进行点积运算，其中X1 和 X2 对应的维度（通俗点说，第一个矩阵的列数，和第二个矩阵的行数要相等）的元素个数必须保持一致，计算过程见下图

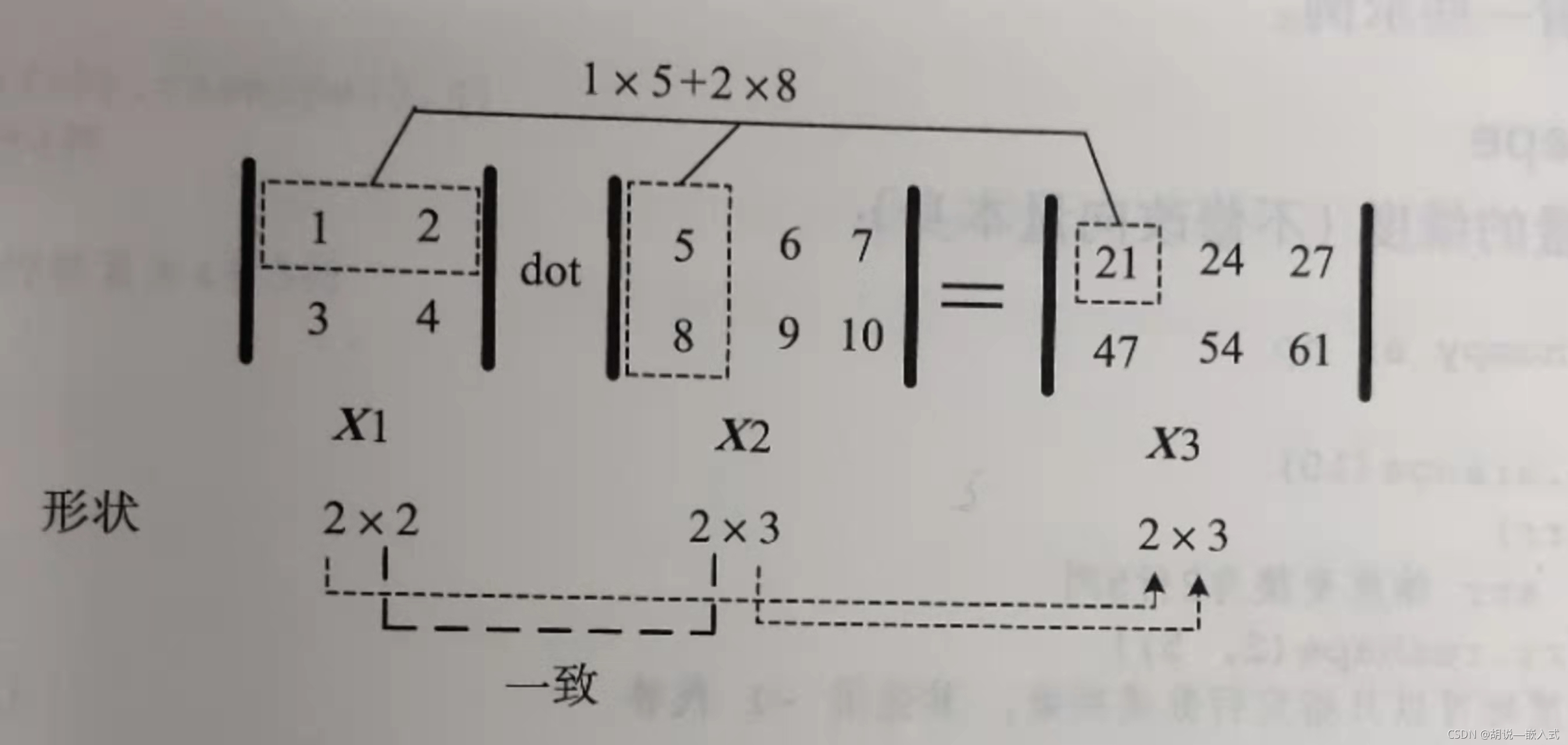
 在numpy中点积运算，用np.dot表示，其一般格式为：
numpy.dot(a , b , out = None)

X1 = np.array([[1,2], [3,4]])
X2 = np.array([[5, 6, 7], [8, 9, 10]])
result = dot(X1, X2)
print(result)"""计算结果为 ：[[21,24,27][47,54,61]]
"""