系列文章链接
参考数据集讲解：数据基础：多维时序数据集简介
论文一：2022 Anomaly Transformer：异常分数预测
论文二：2022 TransAD：异常分数预测
论文三：2023 TimesNet：基于卷积的多任务模型

论文链接：TimesNet.pdf
代码库链接：https://github.com/thuml/Time-Series-Library
项目介绍：https://github.com/thuml/TimesNet
参考作者解读：ICLR2023 | TimesNet: 时序基础模型，预测、填补、分类等五大任务领先

本文和Anomaly Transformer都是清华大学的团队，也是同一个作者。本文研究基于深度学习异常检测有两个背景：

1. 基于RNN或者CNN的算法，很难捕捉到时序数据的长期以来关系，因此都只能针对局部窗口内的数据进行建模，这个观点和TransAD是一样的；
2. 近年来transformer表现出了提取时序数据长期依赖关系（如：周期性、季节性等）的优势，因此能够基于transformer进行依赖关系提取，但是简单的分散点位很难作为这种长序列依赖关系的强有力的表征，而且时序数据的周期性会受到多种周期性因素（天气、节假日等）的影响，因此需要考虑如何处理这种多周期变化带来的影响；

基于上述两点思考，作者提出了TimesNet这样的模型架构，具体创新点表现如下：

• 一维到二维的时序数据转换：将一维的时间序列转换成二维的数据表征，同时对时序数据周期内（连续邻近点位变化）和周期间（长期规律性变化）的变化进行建模；对于一个长度为$T$、通道数为$C$的一维时间序列$X_{1D}\in {\mathbb{R}}^{T\ast C}$，对于长时间序列而言，其周期性可以通过傅立叶变换计算得到：$$\mathbf{A}=Avg(Amp(FFT(X_{1D})))$$ f 1 , . . . f k = a r g f ∗ ∈ { 1 , . . . , [ T 2 ] } A f_1,...f_k=\underset {f_*\in \{1,...,[\frac {T}{2}]\}}{arg} \bold A f1​,...fk​=f∗​∈{1,...,[2T​]}arg​A$$p_1,...p_k=[\frac{T}{f_x}],...,[\frac{T}{f_k}]$$其中$\mathbf{A}$代表了一维时间序列中每个频率分量的强度，强度最大的$k$个频率 { f 1 , . . . f k } \{f_1,...f_k\} {f1​,...fk​}对应最显著的$k$个周期长度 { p 1 , . . . p k } \{p_1,...p_k\} {p1​,...pk​}，上述过程简记如下： A , { f 1 , . . . f k } , { p 1 , . . . p k } = P e r i o d ( X 1 D ) \bold A,\{f_1,...f_k\},\{p_1,...p_k\}=Period(X_{1D}) A,{f1​,...fk​},{p1​,...pk​}=Period(X1D​)这样基于上述计算就可以根据不同的周期长度进行计算出不同的二维张量表示： X 2 D i = R e s h a p e p i , f i ( P a d d i n g ( X 1 D ) ) , i ∈ { 1 , . . . k } X_{2D}^i=Reshape_{p_i,f_i}(Padding(X_{1D})),i\in\{1,...k\} X2Di​=Reshapepi​,fi​​(Padding(X1D​)),i∈{1,...k}其中Padding 操作是为了保持张量维度的一致性；$X_{2D}^i$就可以表示在频率$f_i$、周期长度$p_i$的基础上转换的第$i$个二维张量，行和列分别表示周期内和周期间的变化，经过这个转换，一维的时间序列数据就可以被转换成$k$个不同频率和周期下的二维的张量集合 { X 2 D 1 , . . . X 2 D k } \{X_{2D}^1,...X_{2D}^k\} {X2D1​,...X2Dk​}，经过这种转换，就可以采用二维卷积核来进行特征提取；
  
  
• TimesBlock：在完成一维到二维的转换后，采用Inception模型进行二维的张量集合处理（简化了一下表示，具体看原文）：$${\hat{X}}_{2D}=Inception(X_{2D})$$然后就像残差模块的处理一样，通过聚合将卷积后的数据转换到一维空间：$${\hat{X}}_{1D}=Trunc(Reshap{e}_{1,p\ast f}({\hat{X}}_{2D}))$$然后采用加权求和的方式得到最终的输出：
  
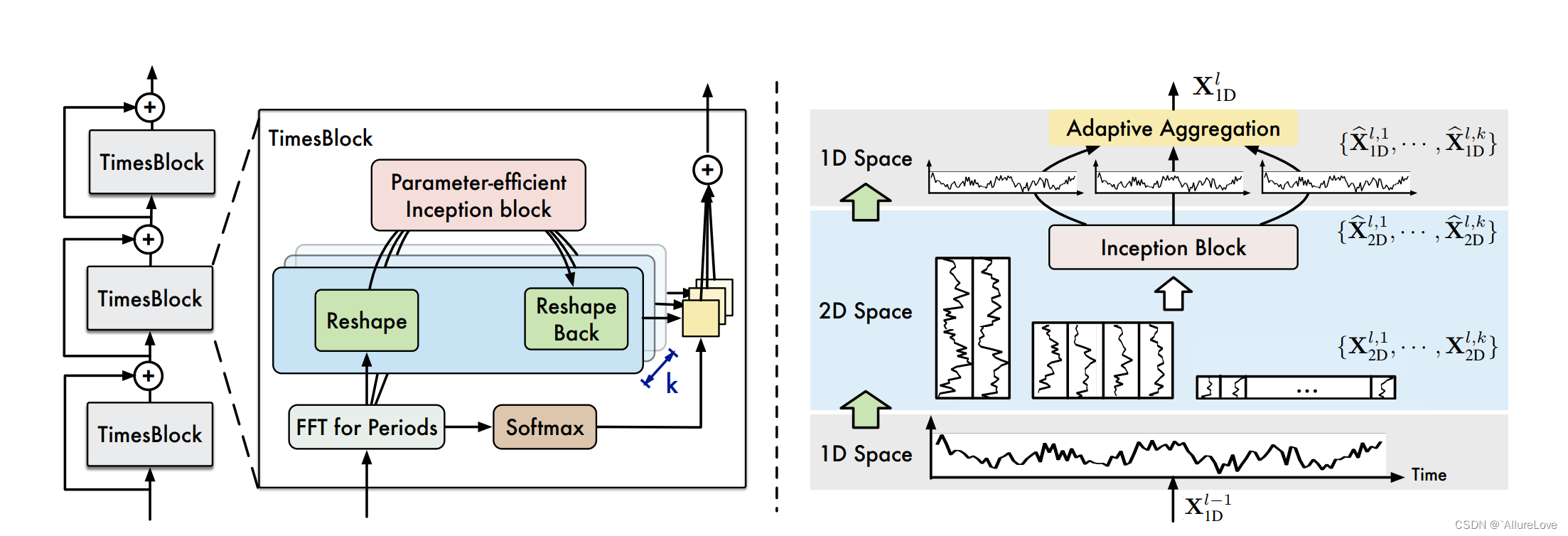
  该模型可以应用于多种任务：时序数据分类、预测、异常检测、缺失值填充等，从实验效果来看很全能；