从产品代码的安全角度考虑，我们需要对代码、数据进行加密。加密的算法有很多种，基于速度考虑，我们一般使用对称加密算法，其中有一种常见的对称加密算法：AES(Advanced Encryption Standard)。在一些高端的MCU，如I.MX RT1176中，AES直接集成到了硬件中，它有一个OTFAD实时解密引擎，可以将保存在NOR Flash中使用AES加密的代码边解密边运行，可见AES加密的可靠性和重要性。所以本节就来介绍一下AES加密算法的原理。

1 简介

AES加密算法(也称为Rijndael算法)是一种对称分块密码算法，以块为单位对数据进行加密，一个块的大小为128位。而AES的密钥则可以为128、192和256位。不同的密钥长度对应着不同的加密轮数：128位为10轮、192位为12轮、256位为14轮。AES基于替代-置换网络，也称为SP网络。它由一系列链接操作组成，包括将输入替换为特定的输出(替代)以及涉及位排序(置换)的其他操作。

AES有如下特点：

• SP网络：与DES算法中的Feistel密码结构不同，它采用了SP网络结构。
• 密钥扩展：在第一阶段，它仅采用一个密钥，然后扩展为用于各个轮次的多个密钥
• 字节数据：AES加密算法对字节数据进行操作，而不是位数据。在加密过程中，将128位块大小视为16个字节。
• 密钥长度：要执行的轮次取决于用于加密数据的密钥长度。128位密钥长度有十轮，192位密钥长度有12轮，256位密钥长度有14轮。

2 AES算法

2.1 AES如何工作

要理解AES的工作方式，首先需要了解它是如何在多个步骤之间传输数据的。由于单个块是16字节，因此我们用一个4x4矩阵(也叫状态数组)保存数据，每个单元保存1个字节的信息。

对于128位的密钥，加密过程中需要执行16轮操作。每一轮操作都需要使用一个不同的轮密钥。轮密钥是通过对初始密钥进行一系列变换生成的，这个在后面的例子中详细介绍。根据AES标准规定，对于128位密钥，需生成10个轮密钥，用于不同轮次的AES加密操作。

2.2 AES计算步骤

流程图如下：

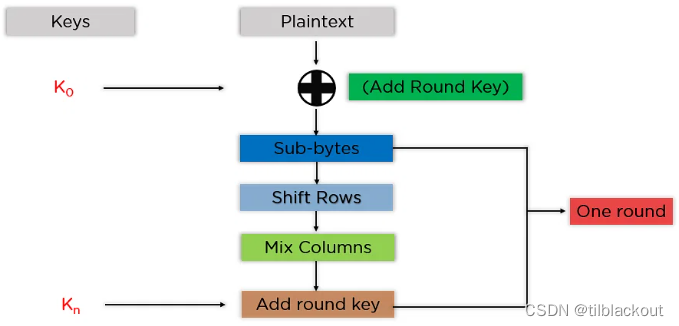
这些步骤需要依次对每个块进行操作。成功加密每个块后，将它们组合在一起形成最终的密文。具体步骤如下：

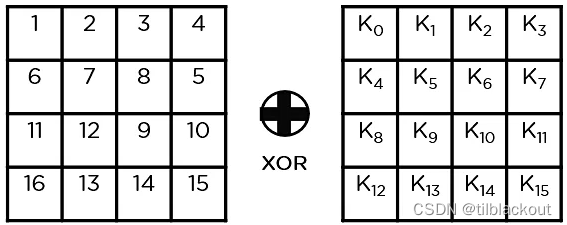
（1）添加轮密钥(Add Round Key)
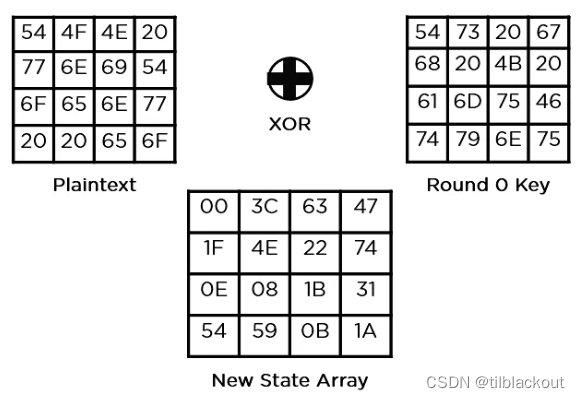
使用生成的第一个密钥(K0)，通过与状态数组中存储的块数据进行异或运算。将得到的状态数组作为下一步的输入。

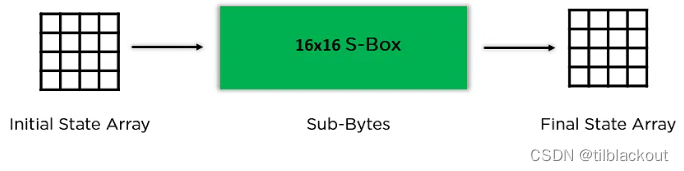
（2）字节替换(Sub-Bytes)
在这个步骤中，将状态数组的每个字节转换为十六进制，分为两个4位的数。通过一个替代盒(S-Box)映射生成最终状态数组的新值，其中高四位(行数)和低四位(列数)作为索引，在S-Box中查找对应的字节进行替换。

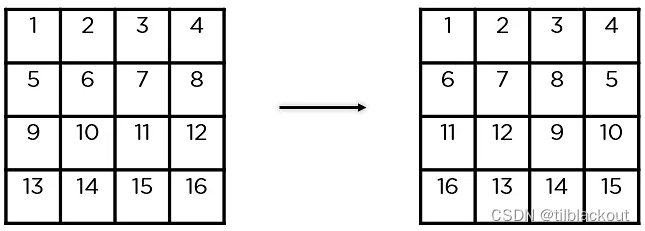
（3）行移位(Shift Rows)
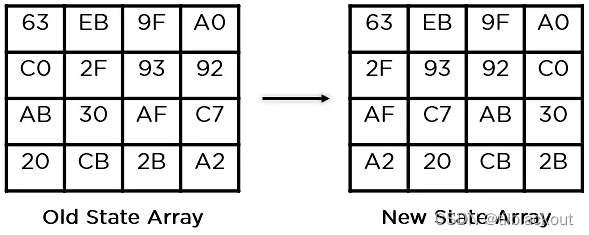
它交换行元素之间的位置。第一行不动，第二行循环左移1位，第三行循环左移2位，第四行循环左移3位。

（4）列混合变换(Mix Columns)
将一个预定义的常数矩阵与状态数组中的每一列进行乘法运算，从而得到下一状态数组中的新列。通过对状态数组中的所有列都执行与相同常数矩阵的乘法运算，最终得到下一步的状态数组。这个步骤在最后一轮中不执行。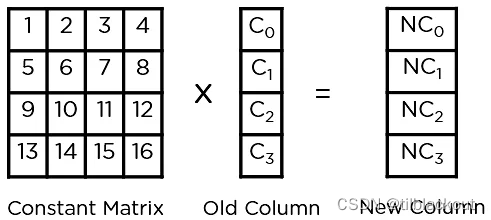

• 注意：这里的运算并不是传统的矩阵乘法，这个在后面的例子中讲解

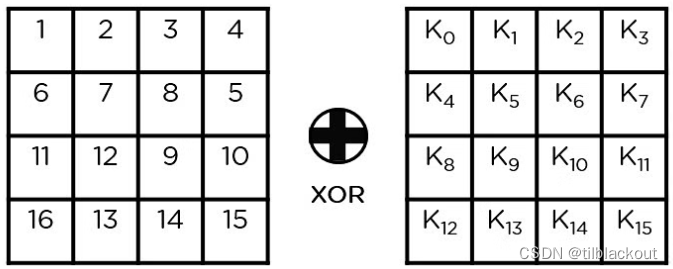
（5）添加轮密钥(Add Round Key)
将轮次对应的密钥与前一步得到的状态数组进行异或运算。如果这是最后一轮，则得到的状态数组将成为特定块的密文；否则，它将作为下一轮的新状态数组输入。

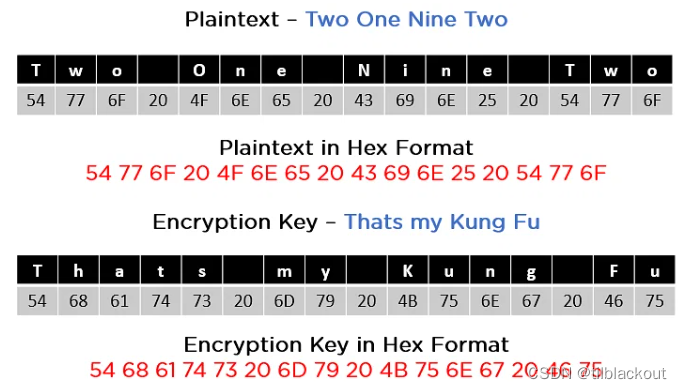
2.3 实例

假设明文为Two One Nine Two，而加密密钥为Thats my Kung fu，我们需要使用它们的16进制来进行计算，它们的长度都是128bit，如下图所示：

接着我们生成接下来10轮的扩展密钥(轮密钥)：

所有的轮密钥都是从Round 0密钥进行扩展的，首先将每一列从0开始索引：

我们根据以下公式可以一列一列地求出后面的轮密钥：
如果这个索引不是4的倍数，则$W_i=W_{i-4}\oplus W_{i-1}$。
如果索引是4的倍数，则$W_i=W_{i-4}\oplus T(W_{i-1})$。其中T函数包括：
①字循环：假设$W_{i-1}$从上到下为$[a_1,a_2,a_3,a_4]$，则字循环后为$[a_2,a_3,a_4,a_1]$
②字节代换：将字循环的结果使用S盒进行字节代换
③轮常量异或：将字循环的结果、字节代换的结果和轮常量三者进行异或得到最终的$T(W_{i-1})$，其中轮常量是一个固定的10×4的矩阵

（1）添加轮密钥(Add Round Key)

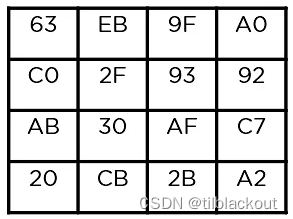
（2）字节替换(Sub-Bytes)：通过一个16x16的S-Box进行字节替换
这里就不列出S-Box的原型了，假设最终的结果如下：

（3）行移位(Shift Rows)

（4）列混合变换(Mix Columns)

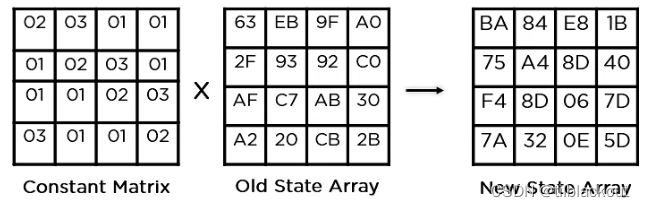
这里以得出状态矩阵的第一个元素0xBA为例，看看是怎么计算得到的：
$\text{ res }=(2\times 0\text{x}63)+(3\times 0\text{x}2F)+0\text{x}AF+0\text{x}A2=0\text{x}BA$
根据AES的规定，这里有两个地方需要转化：第一个加法需要转为异或运算，第二个乘法的运算的转换有些复杂，规则如下：
$$\begin{array}{rl}& (00000010)\times \left(a_7{a}_6{a}_5{a}_4{a}_3{a}_2{a}_1{a}_0\right)=\{\begin{array}{c}\left(a_6{a}_5{a}_4{a}_3{a}_2{a}_1{a}_{0}0\right),a_7=0\\ \left(a_6{a}_5{a}_4{a}_3{a}_2{a}_1{a}_{0}0\right)\oplus (00011011),a_7=1\end{array}\\ & (00000011)\times \left(a_7{a}_6{a}_5{a}_4{a}_3{a}_2{a}_1{a}_0\right)=[(00000010)\oplus (00000001)]\times \left(a_7{a}_6{a}_5{a}_4{a}_3{a}_2{a}_1{a}_0\right)\\ & =\left[(00000010)\times \left(a_7{a}_6{a}_5{a}_4{a}_3{a}_2{a}_1{a}_0\right)\right]\oplus \left(a_7{a}_6{a}_5{a}_4{a}_3{a}_2{a}_1{a}_0\right)\end{array}$$
乘法运算需要将数转化为二进制，上图中第一个公式为2乘以一个uint8的数的规则。第二行为3乘以一个uint8的数的规则，实际上就是根据乘法分配率转变为第一个公式。
我们现在就来计算一下上面的两个乘法：
$$\begin{array}{rl}& 2\times 0\text{x}63=(00000010)b\times (01100011)b=(11000110)b=0\times C6\\ & 3\times 0\text{x}2F=\left[(00000010)b\times (00101111)b\right]\oplus (0010111)b=(01011110)b\oplus (00101111)b=(01110001)b=0\times 71\\ & \text{ res }=0\text{x}C6\oplus 0\text{x}71\oplus 0\text{x}AF\oplus 0\text{x}A2=0\text{x}BA\end{array}$$

（5）添加轮密钥(Add Round Key)：这一步异或上前面的Round 1密钥

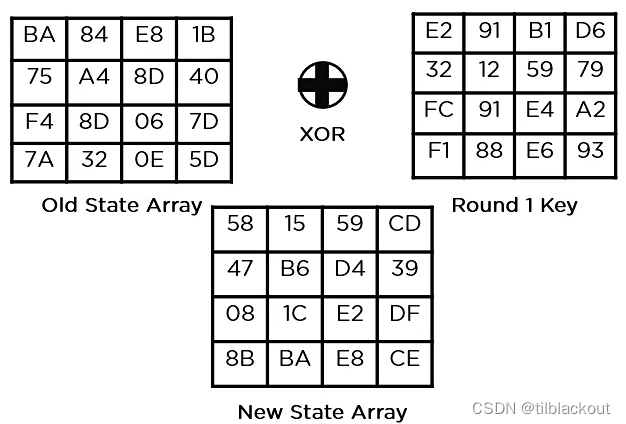
这个状态数组将成为下一轮的输入，根据密钥的长度，重复上述步骤，直到完成第10轮，就得到了最终的密文。

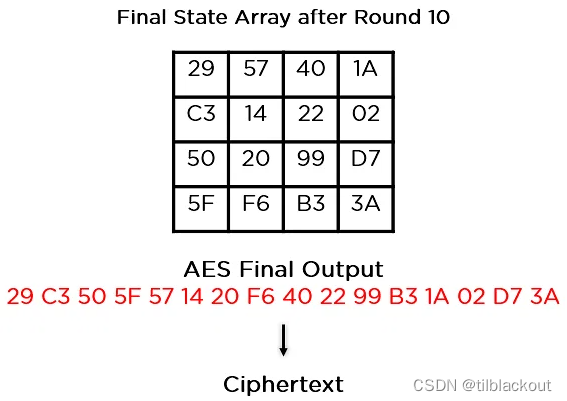
3 总结

AES算法用于加密与解密数据，在计算机领域中具有高度的安全性和效率。AES算法的数据块大小为128位，密钥长度可以是128位、192位或256位。算法在加密过程中使用了不同的轮数，这些轮数也根据密钥长度的不同而有所变化。本文对AES加密的原理做了一个简单的介绍，并举了一个简单的例子。和我之前写的CRC、MD5的博客一样，有了原理后一定要在代码中实现，这才是理论的意义，这也能帮我们更深入地理解代码。所以下一节，我将深入地剖析一下AES的代码实现。