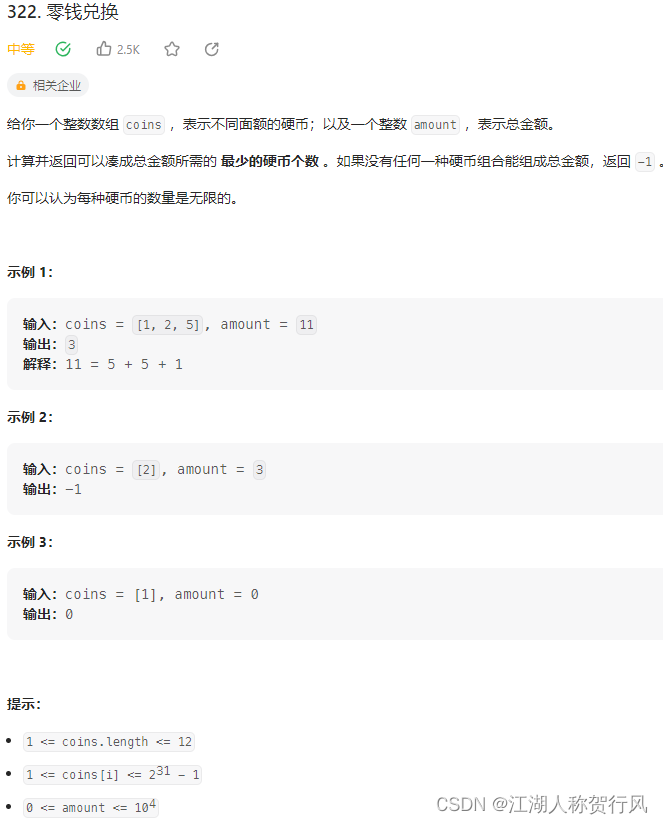
题目来源:https://leetcode.cn/problems/coin-change/description/
C++题解(来源代码随想录):题目中说每种硬币的数量是无限的,可以看出是典型的完全背包问题。动规五部曲分析如下:
- 确定dp数组以及下标的含义。dp[j]:凑足总额为j所需钱币的最少个数为dp[j]
- 确定递推公式。凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j]。递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
- dp数组如何初始化。首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0; 其他下标对应的数值呢?考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。所以下标非0的元素都是应该是最大值。
- 确定遍历顺序。本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。
- 举例推导dp数组
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX);dp[0] = 0;for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包if (dp[j - coins[i]] != INT_MAX) { // 如果dp[j - coins[i]]是初始值则跳过,不跳过+1会超出int范围。dp[j] = min(dp[j - coins[i]] + 1, dp[j]);}}}if (dp[amount] == INT_MAX) return -1;return dp[amount];}
};