OpenCV-Python中的图像处理-傅里叶变换
- 傅里叶变换
- Numpy中的傅里叶变换
- Numpy中的傅里叶逆变换
- OpenCV中的傅里叶变换
- OpenCV中的傅里叶逆变换
- DFT的性能优化
- 不同滤波算子傅里叶变换对比
傅里叶变换
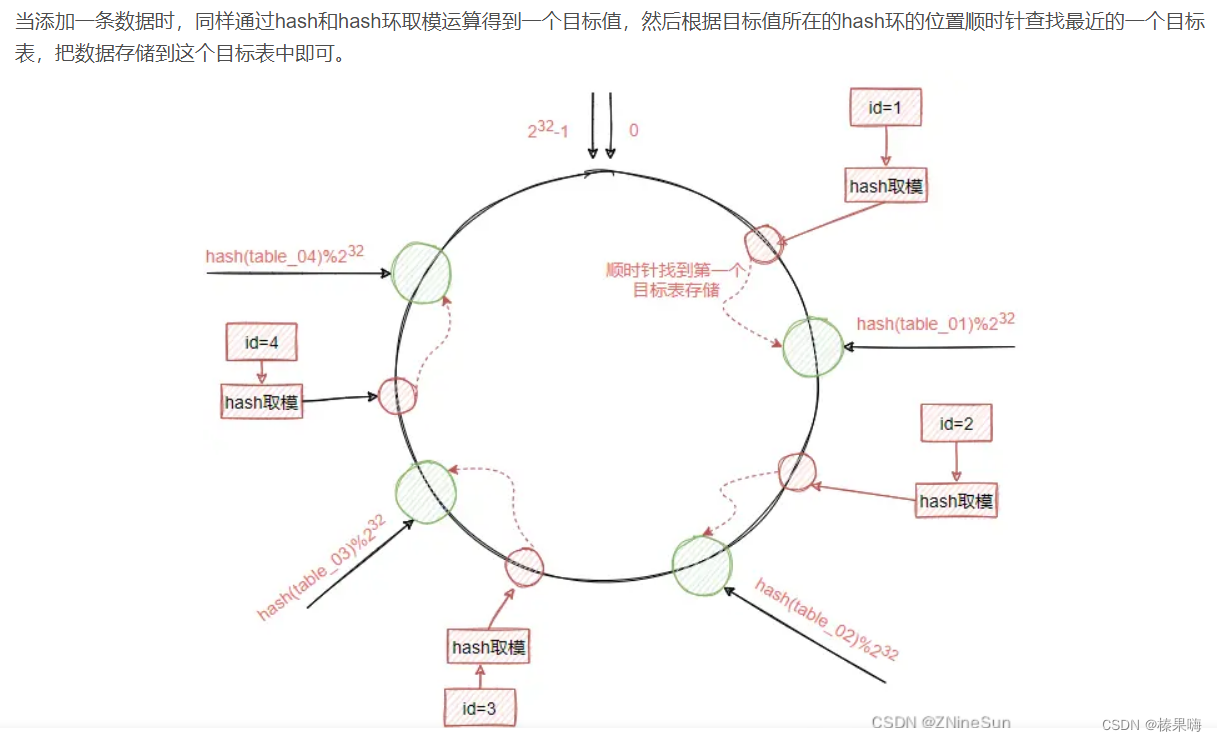
- 傅里叶变换经常被用来分析不同滤波器的频率特性。我们可以使用 2D 离散傅里叶变换 (DFT) 分析图像的频域特性。实现 DFT 的一个快速算法被称为快速傅里叶变换( FFT)。
- 对于一个正弦信号:x (t) = A sin (2πft), 它的频率为 f,如果把这个信号转到它的频域表示,我们会在频率 f 中看到一个峰值。如果我们的信号是由采样产生的离散信号组成,我们会得到类似的频谱图,只不过前面是连续的,现在是离散。你可以把图像想象成沿着两个方向采集的信号。所以对图像同时进行 X 方向和 Y 方向的傅里叶变换,我们就会得到这幅图像的频域表示(频谱图)。
- 对于一个正弦信号,如果它的幅度变化非常快,我们可以说他是高频信号,如果变化非常慢,我们称之为低频信号。你可以把这种想法应用到图像中,图像那里的幅度变化非常大呢?边界点或者噪声。所以我们说边界和噪声是图像中的高频分量(注意这里的高频是指变化非常快,而非出现的次数多)。如果没有如此大的幅度变化我们称之为低频分量。
Numpy中的傅里叶变换
Numpy 中的 FFT 包可以帮助我们实现快速傅里叶变换。函数 np.fft.fft2() 可以对信号进行频率转换,输出结果是一个复杂的数组。本函数的第一个参数是输入图像,要求是灰度格式。第二个参数是可选的, 决定输出数组的大小。输出数组的大小和输入图像大小一样。如果输出结果比输入图像大,输入图像就需要在进行 FFT 前补0。如果输出结果比输入图像小的话,输入图像就会被切割。
f = np.fft.fft2(img)
现在我们得到了结果,频率为 0 的部分(直流分量)在输出图像的左上角。如果想让它(直流分量)在输出图像的中心,我们还需要将结果沿两个方向平移 N/2 。函数 np.fft.fftshift() 可以帮助我们实现这一步。(这样更容易分析)。进行完频率变换之后,我们就可以构建振幅谱了。
fshift = np.fft.fftshift(f)
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)
f = np.fft.fft2(img)
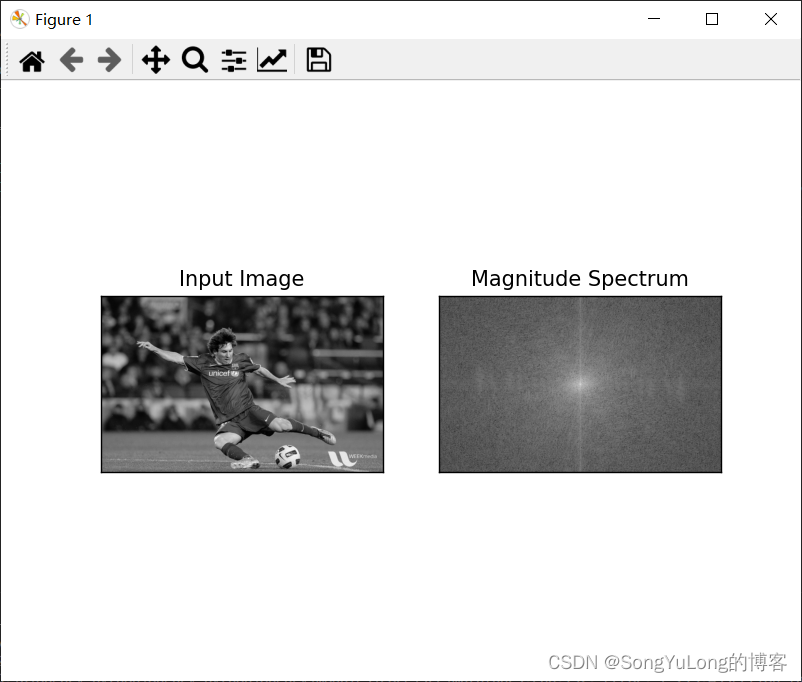
fshift = np.fft.fftshift(f)# 构建振幅图
magnitude_spectrum = 20*np.log(np.abs(fshift))plt.subplot(121), plt.imshow(img, cmap='gray'), plt.title('Input Image')
plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray'), plt.title('Magnitude Spectrum')
plt.show()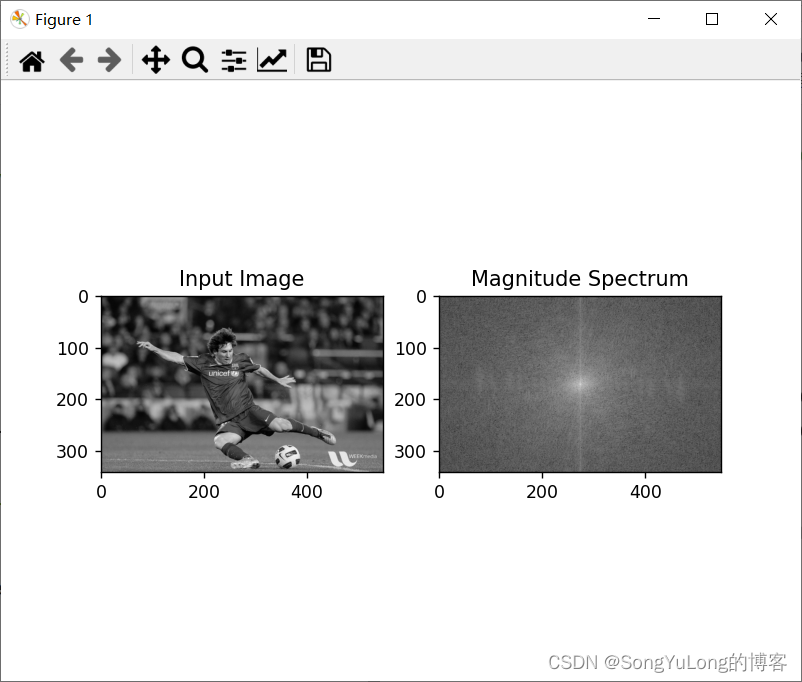
我们可以看到输出结果的中心部分更白(亮),这说明低频分量更多。
Numpy中的傅里叶逆变换
- 对图像进行FFT变换之后得到频域图像数据,然后再做IFFT变换又可以得到原始图像。相关函数:np.fft.ifftshift(),np.fft.ifft2()
fishift = np.fft.ifftshift(fshift)
img_ifft = np.fft.ifft2(fishift) - 我们可以对频域图像数据进行操作以实现一些图像处理效果,如在频域内将低频分量的值设为0,可以实现对图像的高通滤波处理:
rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)# 1.在Numpy内对图像进行傅里叶变换,得到其频域图像
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
# 这里是构建振幅图,显示图像频谱
magnitude_spectrum = 20*np.log(np.abs(fshift))# 2.IFFT 将频域图像还原成原始图像,这里只是验证FFT的逆运算
fishift = np.fft.ifftshift(fshift)
img_ifft = np.fft.ifft2(fishift)
img_ifft = np.abs(img_ifft) # 取绝对值,否则不能用imshow()来显示图像# 3.在频域内将低频分量的值设为0,实现高通滤波。
rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)
fshift[crow-30:crow+30, ccol-30:ccol+30] = 0 # 4.对高通滤波后的图像频域数据进行逆傅里叶变换,得到高通滤波后图像。
f_ishift = np.fft.ifftshift(fshift)
img_back = np.fft.ifft2(f_ishift)
img_back = np.abs(img_back) # 取绝对值,否则不能用imshow()来显示图像
# 构建高通滤波后的振幅图,显示图像频谱
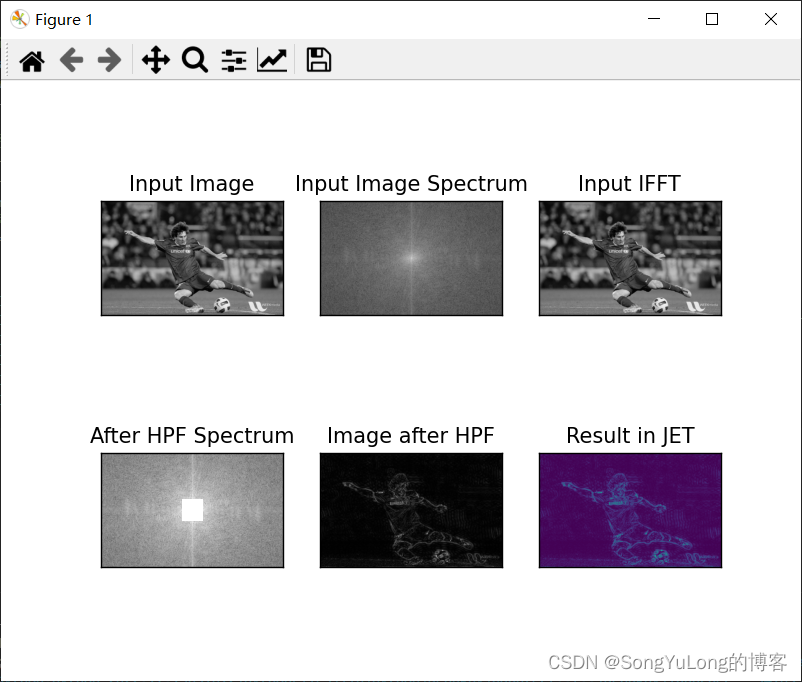
after_sepctrum = 20*np.log(np.abs(fshift))plt.subplot(231), plt.imshow(img, cmap='gray'), plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(232), plt.imshow(magnitude_spectrum, cmap='gray'), plt.title('Input Image Spectrum'), plt.xticks([]), plt.yticks([])
plt.subplot(233), plt.imshow(img_ifft, cmap='gray'), plt.title('Input IFFT'), plt.xticks([]), plt.yticks([])
plt.subplot(234), plt.imshow(after_sepctrum, cmap='gray'), plt.title('After HPF Spectrum'), plt.xticks([]), plt.yticks([])
plt.subplot(235), plt.imshow(img_back, cmap='gray'), plt.title('Image after HPF'), plt.xticks([]), plt.yticks([])
plt.subplot(236), plt.imshow(img_back), plt.title('Result in JET'), plt.xticks([]), plt.yticks([])
plt.show()
OpenCV中的傅里叶变换
OpenCV 中相应的函数是 cv2.dft() 和 cv2.idft()。和前面输出的结果一样,但是是双通道的。第一个通道是结果的实数部分,第二个通道是结果的虚数部分。输入图像要首先转换成 np.float32 格式。
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0], dft_shift[:,:,1]))plt.subplot(121), plt.imshow(img, cmap='gray'), plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray'), plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()
OpenCV中的傅里叶逆变换
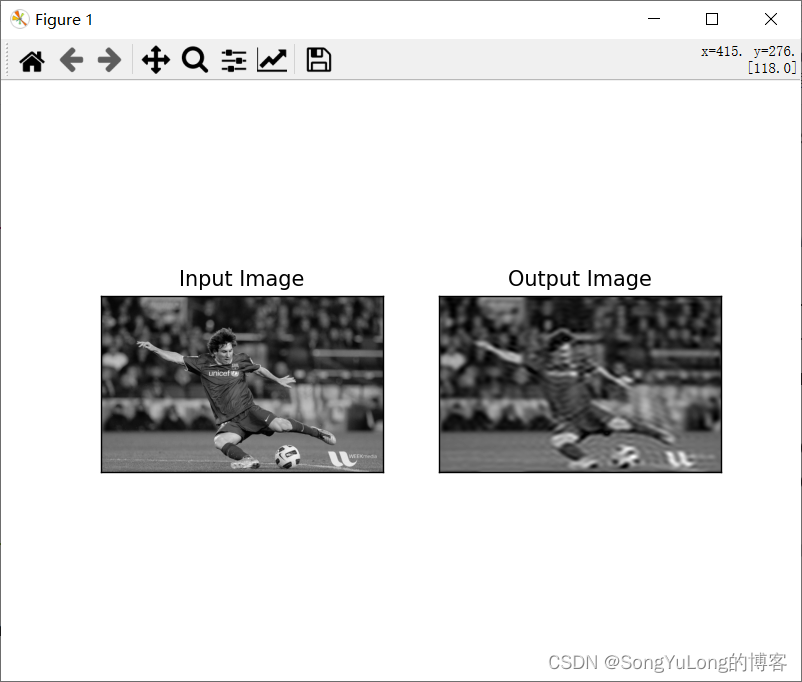
前面的部分我们实现了一个 HPF(高通滤波)高通滤波其实是一种边界检测操作。现在我们来做 LPF(低通滤波)将高频部分去除。其实就是对图像进行模糊操作。首先我们需要构建一个掩模,与低频区域对应的地方设置为 1, 与高频区域对应的地方设置为 0。
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)
# 1.OpenCV中做DFT
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)rows, cols = img.shape
crow, ccol = int(rows/2), int(cols/2)# create a mask first, center square is 1, remaining all zeros
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1# apply mask and inverse DFT
fshift = dft_shift*mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:,:,0], img_back[:,:,1])plt.subplot(121), plt.imshow(img, cmap='gray'), plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(img_back, cmap='gray'), plt.title('Output Image'), plt.xticks([]), plt.yticks([])
plt.show()
DFT的性能优化
- 当数组的大小为某些值时 DFT 的性能会更好。当数组的大小是 2 的指数时 DFT 效率最高。当数组的大小是 2, 3, 5 的倍数时效率也会很高。所以如果你想提高代码的运行效率时,你可以修改输入图像的大小(补 0)。对于OpenCV 你必须自己手动补 0。但是 Numpy,你只需要指定 FFT 运算的大小,它会自动补 0。
- OpenCV 提供了一个函数:cv2.getOptimalDFTSize()来确定最佳大小。它可以同时被 cv2.dft() 和 np.fft.fft2() 使用。
import numpy as np
import cv2img = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)
rows,cols = img.shape
print('原始图像大小:',rows, cols)
nrows = cv2.getOptimalDFTSize(rows)
ncols = cv2.getOptimalDFTSize(cols)
print('DFT最佳大小:',nrows, ncols)
原始图像大小: 342 548
DFT最佳大小: 360 576
import numpy as np
import cv2
from matplotlib import pyplot as pltimg = cv2.imread('./resource/opencv/image/messi5.jpg', cv2.IMREAD_GRAYSCALE)
rows,cols = img.shape
print('原始图像大小:',rows, cols)
nrows = cv2.getOptimalDFTSize(rows)
ncols = cv2.getOptimalDFTSize(cols)
print('DFT最佳大小:',nrows, ncols)# Numpy数组操作,原图扩大到最佳DFT size
nimg = np.zeros((nrows, ncols))
nimg [:rows, :cols] = img#
right = ncols - cols
bottom = nrows - rows
# just to avoid line breakup in PDF file
mimg = cv2.copyMakeBorder(img, 0, bottom, 0, right, cv2.BORDER_CONSTANT, value=0)plt.subplot(231), plt.imshow(img, cmap='gray')
plt.subplot(232), plt.imshow(nimg, cmap='gray')
plt.subplot(233), plt.imshow(mimg, cmap='gray')
plt.show()
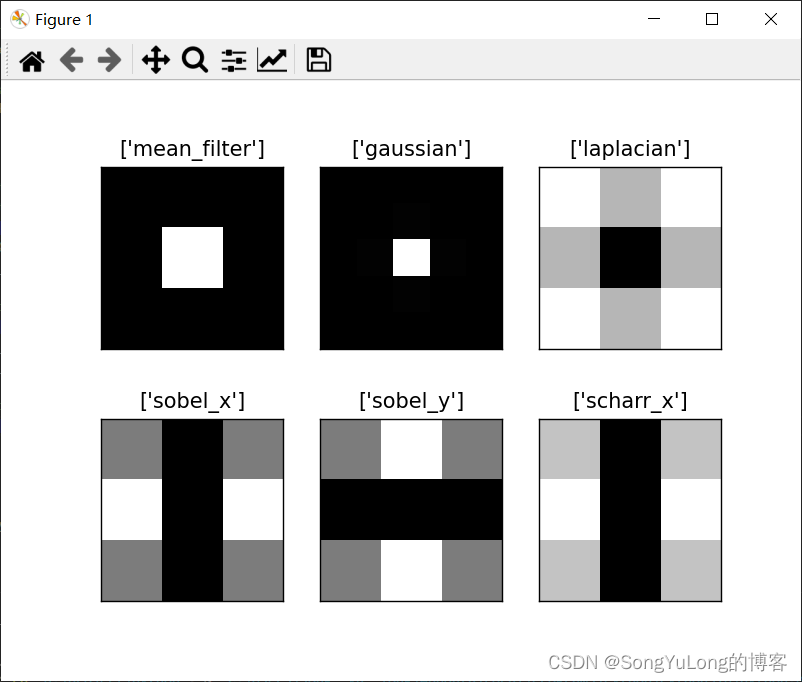
不同滤波算子傅里叶变换对比
为什么拉普拉斯算子是高通滤波器?为什么 Sobel 是 HPF?等等。对于第一个问题的答案我们以傅里叶变换的形式给出。我们一起来对不同的算子进行傅里叶变换并分析它们:
import numpy as np
import cv2
from matplotlib import pyplot as plt# simple averaging filter whitout scaling parameter
mean_filter = np.ones((3,3))# creating a guassian filter
x = cv2.getGaussianKernel(5, 10)
# x.T 为矩阵转置
gaussian = x*x.T# different edge detecting filters
# scharr in x-direction
scharr = np.array([[-3, 0, 3],[-10, 0, 10],[-3, 0, 3]])# sobel in x direction
sobel_x = np.array([[-1, 0, 1],[-2, 0, 2],[-1, 0, 1]])# sobel in y direction
sobel_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])# laplacian
laplacian = np.array([[0, 1, 0], [1, -4, 1],[0, 1, 0]])filters = [mean_filter, gaussian, laplacian, sobel_x, sobel_y, scharr]
filter_name = ['mean_filter', 'gaussian', 'laplacian', 'sobel_x', 'sobel_y', 'scharr_x']fft_filters = [np.fft.fft2(x) for x in filters]
fft_shift = [np.fft.fftshift(y) for y in fft_filters]
mag_spectrum = [np.log(np.abs(z)+1) for z in fft_shift]for i in range(6):plt.subplot(2,3,i+1), plt.imshow(mag_spectrum[i], cmap='gray')plt.title([filter_name[i]]), plt.xticks([]), plt.yticks([])
plt.show()