深入篇【C++】手搓模拟实现二叉搜索树(递归/非递归版本)&&常见应用场景
- Ⅰ.二叉搜索树概念
- Ⅱ.二叉搜索树模拟实现(递归与非递归)
- ①.定义结点
- ②.构造二叉树
- ③.插入结点
- ④.删除结点(重要)
- ⑤.查找结点
- ⑥.析构二叉树
- ⑦.拷贝二叉树
- ⑧.二叉树赋值
- Ⅲ.二叉搜索树应用
- ①.K模型与KV模型
Ⅰ.二叉搜索树概念
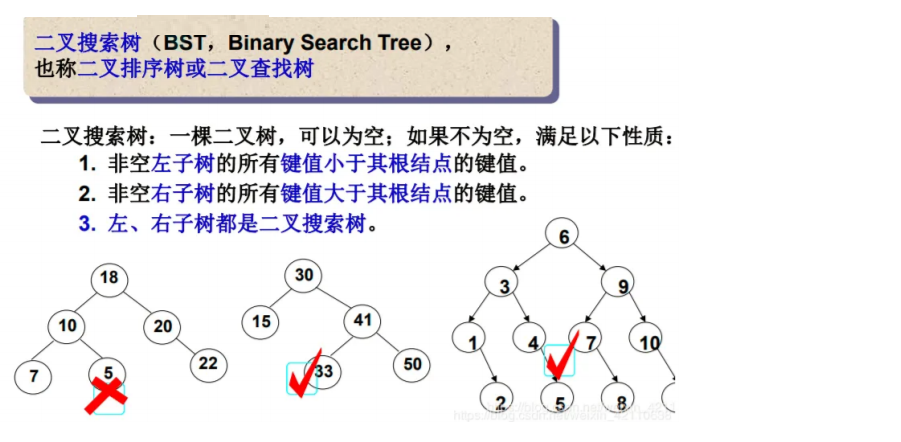
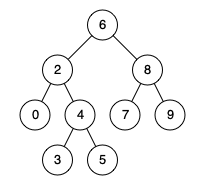
二叉搜索树又称二叉排序树,它或者是一颗空树或者是具有以下性质的二叉树:
1.当它的左子树不为空,则左子树上所有的结点的值都要小于根节点。
2.当它的右子树不为空,则右子树上所有的结点的值都要大于根结点。
3.它的左右子树都是二叉搜索树。
Ⅱ.二叉搜索树模拟实现(递归与非递归)
①.定义结点
二叉树的结点:含有左右指针和数据的结点。
template <class K>struct BSTreeNode//定义二叉树结点{BSTreeNode<K>* left;BSTreeNode<K>* right;K _key;BSTreeNode(const K& key)//初始化:_key(key), left(nullptr), right(nullptr){}};
②.构造二叉树
结点定义出来后,就用二叉树的形式组织起来,封装一个指向结点的指针。
一开始需要初始化:
template <class K>struct BSTree{typedef BSTreeNode<K> Node;BSTree()//构造函数,初始化:_root(nullptr){}private:Node* _root;//封装一个指向结点的指针 }
③.插入结点
1.非递归版本:
插入结点的方法很简单,当这颗树为空树时,直接开辟出一个结点给它。当这颗树不为空时,则按照二叉搜索树的特性来比较,将插入结点插入到正确位置。
1.当插入的结点值key要比根结点大,则key需要到根的右树进行比较,当key的值比根结点小,则key需要到根的左树进行比较,当key的值与根结点相同时,则返回fasle,按照这样的方式循环下去,当要比较的结点为空时,则就可以将结点插入到这个位置上了。每次比较中都要记录父节点的位置,因为最后需要链接起来。
2.最后链接起来需要和父结点比较一下才能知道链接到父节点的左边还是右边。如果大于父节点则链接到右边,如果小于父节点则连接到左边。
bool insert(const K& key){if (_root == nullptr){_root = new Node(key);}else{Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key < key){parent = cur;cur = cur->right;}else if (cur->_key > key){parent = cur;cur = cur->left;}else{return false;}}if (parent->_key < key){parent->right = new Node(key);}if (parent->_key > key){parent->left = new Node(key);}}return true;}
2.递归版本
我们要知道递归每次都要改变结点的位置,我们就必须要传结点(结点指针)作为参数,但在类外面,我们想要调用递归函数,也需要传结点指针了,但这里结点指针被封装起来不能访问,所以不能直接用一个递归函数就能完成,需要靠一个子函数来获取结点指针。而真正的递归函数就不需要手动传结点指针啦。
1.当根节点为空时,直接开辟出结点给它。
2.当根结点不为空时,就要将key与结点值进行比较,当key大于结点值时,就要转化为子问题,递归到右子树进行比较,当key小于结点值时,就递归到左子树进行比较,当key等于结点值时,就返回false。
3.当递归结束时,就可以将开辟好结点链接起来。(递归的过程就是不断的在创建结点,回来的过程就是不断地将结点链接起来)。
4.这里不需要像非递归那样,每次比较都需要记录父节点的位置,我们这里用一个引用就可以轻松解决问题!我们的指针参数使用引用,即子函数的参数是递归函数参数的别名。
这样做就有一个绝妙的关系:root结点是父节点的左指针或者右指针。直接可以将父节点和新开辟的结点链接起来。
bool insertR(const K& key)//每次递归都需要要改变结点的状态,所以必须要传结点的指针过来,这里使用一个子函数{return _insertR(_root, key);}bool _insertR(Node*& root, const K& key){////root是父节点左子树或者右子树的别名if (root == nullptr){root = new Node(key);//将父节点与新结点链接起来}if (root->_key < key){return _insertR(root->right, key);}else if (root->_key > key){return _insertR(root->left, key);}else{return false;}return true;}
④.删除结点(重要)
1.非递归版本
删除结点要比较复杂,因为存在多种情况,当删除的结点只有一个孩子时,当删除的结点没有孩子时,当删除的结点有两个孩子时,要分三种情况讨论。
1.当删除结点没有孩子时,使用托孤法。将父节点与空链接起来。
2.当删除结点只有一个孩子时,使用托孤法,将父节点与孤结点链接起来。
3.当删除结点有两个孩子时,使用找保姆法,找一个可以替代本身的结点。交换这两个结点,删除这个替换结点。
这个保姆结点可以是左子树的最大结点或者是右子树的最小结点。
要删除某个结点,首先需要找到这个结点,按照二叉搜索树的特性来比较查找,key大于结点值,到右树找,key小于结点值,到左树找,当key等于结点值时,就说明找到了。
而找到要删除的结点后,又要分三种情况来讨论,要删除的结点是属于哪种的,是没有孩子结点的?还是只有一个结点的?还是有两个孩子结点的?其实第一种和第二种是可以合并成一种的。
【当存在一个孩子结点时】
当右子树是空时,说明左子树是孤结点。需要将左子树托孤给父节点。(每次比较的时候需要记录父节点位置)。
而托孤给父节点也是有讲究的,因为不知道是将这个孤结点链接到父结点的左边还是右边,我们要注意,当删除结点是父结点的左孩子时,则这个删除结点的任何一个孩子结点都要小于删除结点的父节点,所以必须链接到父节点的左边。而当删除结点是父节点的右孩子时,删除结点的任何一个孩子结点都要大于删除结点的父节点,所以必须链接到父节点的右边。
所以我们根据当前删除结点是父节点的左子树还是右子树来决定将孤结点链接到父节点的哪边。
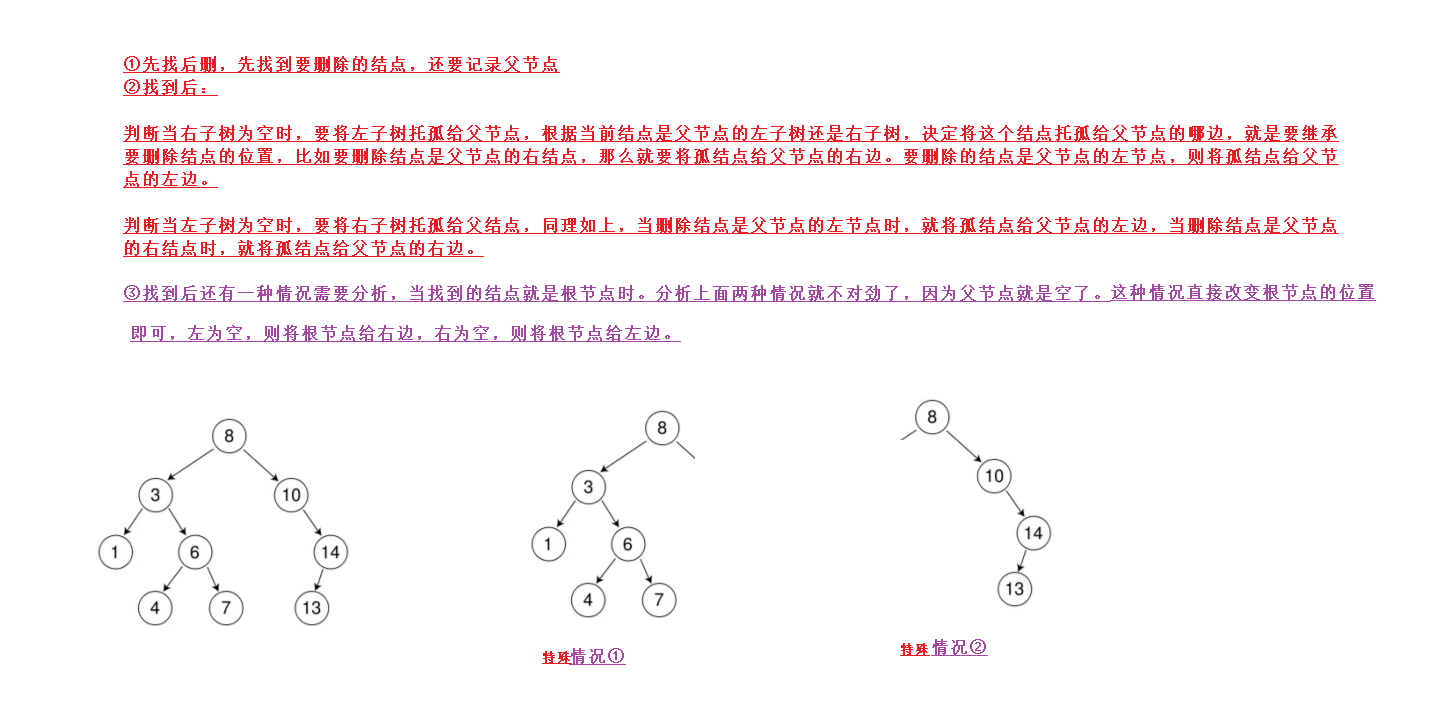
最后还有一种特殊情况比如情况1和情况2,当删除结点是8时,没有左子树或者右子树,但是父节点为空。
所以需要特殊讨论一下。
【当存在两个孩子结点时】
当存在两个孩子结点时,就需要使用保姆法。比如要删除的结点是根节点8,那么它的孩子有两个。我们首先需要找到一个可以替代它的结点,比如左子树的最大结点7,就可以替代它,将它们两个交换。
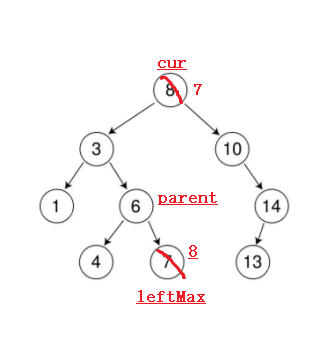
然后删除这个替代结点就可以啦。其实从这里我们就可以观察到,只要找到保姆后,再交换一下,那这个问题就变成要删除的结点只有一个孩子的问题了,因为这个替代结点必定没有右孩子(它是左子树的最大结点,即左子树的最右边).
然后就可以使用托孤法,将这个结点的左子树托孤给父节点即可。

bool erase(const K& key){//首先需要找到要删除的结点,这个过程需要记录父节点Node* cur = _root;Node* parent = nullptr;//父节点一开始为空while (cur){if (cur->_key < key)//特殊情况需要讨论一下{parent = cur;//记录父节点cur = cur->right;}else if (cur->_key > key){parent = cur;//记录父节点cur = cur->left;}else//找到要删除的结点了--cur就是要删除的结点{//1.右子树为空,左子树为孤结点,需要托孤给父节点//特殊情况:当删除结点为根节点时if (cur->right == nullptr) {if (cur == _root){_root = cur->left;//直接往右挪动}else{if (parent->left == cur)//托孤{parent->left = cur->left;}else{parent->left = cur->left;}}}//2.左子树为空,右子树为孤结点,需要托孤给父节点else if (cur->left == nullptr){if (cur == _root)//特殊情况需要讨论一下{_root = cur->right;}else{if (parent->left == cur)//托孤{parent->left = cur->right;}else{parent->right = cur->right;}}}//3.左右子树都存在,找保姆else{//保姆:当前要删除结点的最右结点Node* leftMax = cur->left;Node* parent = cur;//这里不能给nullptrwhile (leftMax->right){parent = leftMax;leftMax = leftMax->right;}//找到保姆后交换std::swap(cur->_key, leftMax->_key);//转化为上面问题--因为最右结点的右结点肯定为空//那左节点就是孤结点,需要托孤if (parent->right == leftMax){parent->right = leftMax->left;}if (parent->left == leftMax){parent->left = leftMax->left;}cur = leftMax;}delete cur;//最后删除这个结点return true;}}return false;}
2.递归版本
递归版本就要比非递归版本简洁多了,只不过有点难理解。这里还是需要子函数来获取结点指针。
要删除某个结点,首先需要找到这个结点。
当key比根结点大的时候,递归到右子树进行比较,当key比根结点值小的时候,递归到左子树进行比较,当key跟结点值相同时,表明找到了。找到后就要分三种情况讨论。
【当存在一个孩子结点时】
不同于非递归版本需要记录父节点,递归版本不需要记录父节点,因为一个引用,让我们省去了很多麻烦。root就是父节点的左指针或者右指针。托孤直接托孤给root即可。因为root就是父节点的左右指针指向。
当右子树不存在时,直接将要删除结点的左子树托孤给root。当左子树不存在时,直接将要删除结点的右子树托孤给root。
【当存在两个孩子结点时】
当存在两个孩子结点时,还是需要使用保姆法,首先找到保姆结点,然后将要删除结点的值与保姆结点值交换。
这样就转化成子问题了。从整棵树来看,因为保姆结点和删除结点交换,而改变了搜索二叉树的特性。不能使用了。
但从左子树来看,还是完整的二叉搜索树,并且要删除结点就只有一个孩子,直接转化为上面的问题。
bool _eraseR(Node*& root, const K& key){//首先还是要先找到要删除的结点if (root == nullptr)return false;if (root->_key < key){return _eraseR(root->right, key);//递归到右子树进行比较}else if (root->_key > key){return _eraseR(root->left,key);//递归到左子树进行比较}else//找到了{Node* del = root;//引用的魅力:root就是父节点左子树或者右子树的引用!,不需要找父节点了//1.左子树为空if (root->left == nullptr){root = root->right;//直接托孤}//2.右子树为空else if (root->right == nullptr){root = root->left;}//3.左右子树都不为空else{//首先找保姆Node* leftMax = root->left;while (leftMax->right){leftMax = leftMax->right;}std::swap(del->_key, leftMax->_key);//转化为子问题//交换完后就不是一个搜索树了,结构被破坏了,但左子树没有,并且这时要删除的结点只有一个结点或者没有结点return _eraseR(root->left, key);//但左子树还是完整的二叉搜索树}delete del;return true;}}
⑤.查找结点
查找二叉树中的某个结点,简单的很,当key的值大于结点值时就递归到右子树去找,当key 的值小于结点的值就递归到左子树去找,当key等于结点值时,就表明找到了,返回true。当找到空则返回false。
bool FindR(const K& key){return _FindR(_root, key);}bool (Node* root, const K& key){if (root == nullptr){return false;}if (root->_key < key){_FindR(root->right, key);}else if (root->_key > key){_FindR(root->left, key);}else{return true;}}
⑥.析构二叉树
对于二叉树的析构,通常使用后序遍历来析构。
遇到空就返回,先析构左子树,再析构右子树,最后析构根结点。
~BSTree(){Destroy(_root);}void Destroy(Node* root){//析构走后序遍历if (root == nullptr)return;Destroy(root->left);//递归析构左子树Destroy(root->right);//递归析构右子树delete root;//析构根结点root = nullptr;}
⑦.拷贝二叉树
拷贝二叉树,我们不能使用insert来一个一个插入,因为inset带有筛选的功能,最后结果顺序会不同的。
我们使用类似于前序遍历的方式,进行拷贝,遍历到哪就相当于拷贝到哪。
首先遇到空就返回。1.拷贝结点 2.递归拷贝左子树3.递归拷贝右子树。4.最后将拷贝结点返回。
BSTree(BSTree<K>& t):_root(nullptr){_root = _Copy(t._root);//前序递归拷贝}Node* _Copy(Node* root)//前序递归拷贝{if (root == nullptr)return nullptr;//根 左子树 右子树Node* newnode = new Node(root->_key);newnode->left = _Copy(root->left);//递归拷贝newnode->right = _Copy(root->right);//递归时,拷贝创建结点,返回时,链接起来return newnode;}
⑧.二叉树赋值
现代写法走起
BSTree<K>* operator=(BSTree<K> t){swap(_root, t._root);return this;}
Ⅲ.二叉搜索树应用
①.K模型与KV模型
1.K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到
的值。即应用在查找某个对象在不在问题。
2… KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。即应用通过一个对象找另外的一个对应的对象问题。
而关联式容器map和set其实就是key_value模型和key模型。
比如查英汉词典就是类似,通过输入英文,而获取对应的中文。
或者计算一盒水果的个数,每种水果有着对应的个数。
比如我们可以将K模型修改成KV模型,就是存两个对象,一个是K,一个是V。
namespace key_value
{template <class K,class V>struct BSTreeNode{BSTreeNode<K,V>* left;BSTreeNode<K,V>* right;K _key;V _value;BSTreeNode(const K& key,const V& value):_key(key),_value(value), left(nullptr), right(nullptr){}};template <class K,class V>struct BSTree{typedef BSTreeNode<K,V> Node;BSTree():_root(nullptr){}BSTree(BSTree<K,V>& t):_root(nullptr){_root = _Copy(t._root);//前序递归拷贝}BSTree<K,V>* operator=(BSTree<K,V> t){swap(_root, t._root);return this;}void Inoder(){_Inoder(_root);}bool insertR(const K& key,const V& value)//每次递归都需要要改变root的状态,所以必须要传root过来,这里使用一个子函数{return _insertR(_root, key,value);}bool eraseR(const K& key){return _eraseR(_root, key);}~BSTree(){Destroy(_root);}Node* FindR(const K& key){return _FindR(_root, key);}private:Node* _FindR(Node* root, const K& key)//key是无法被修改的,value是可以被修改的,所以要传Node* 来修该value{if (root == nullptr){return nullptr;}if (root->_key < key){_FindR(root->right, key);}else if (root->_key > key){_FindR(root->left, key);}else{return root;}}Node* _Copy(Node* root)//前序递归拷贝{if (root == nullptr)return nullptr;//根 左子树 右子树Node* newnode = new Node(root->_key,root->_value,root->_value);newnode->left = _Copy(root->left);//递归拷贝newnode->right = _Copy(root->right);//递归时,拷贝创建结点,返回时,链接起来return newnode;}void Destroy(Node* root){//析构走后序遍历if (root == nullptr)return;Destroy(root->left);Destroy(root->right);delete root;root = nullptr;}bool _eraseR(Node*& root, const K& key){//首先还是要先找到要删除的结点if (root == nullptr)return false;if (root->_key < key){return _eraseR(root->right, key);}else if (root->_key > key){return _eraseR(root->left, key);}else//找到了{Node* del = root;//引用的魅力:root就是父节点左子树或者右子树的引用!,不需要找父节点了//1.左子树为空if (root->left == nullptr){root = root->right;}//2.右子树为空else if (root->right == nullptr){root = root->left;}//3.左右子树都不为空else{//首先找保姆Node* leftMax = root->left;while (leftMax->right){leftMax = leftMax->right;}std::swap(del->_key, leftMax->_key);//转化为子问题//交换完后就不是一个搜索树了,结构被破坏了,但左子树没有,并且这时要删除的结点只有一个结点或者没有结点return _eraseR(root->left, key);}delete del;return true;}}bool _insertR(Node*& root, const K& key,const V& value){//root是父节点左子树或者右子树的别名if (root == nullptr){root = new Node(key,value);}if (root->_key < key){return _insertR(root->right,key,value);}else if (root->_key > key){return _insertR(root->left, key,value);}else{return false;}return true;}void _Inoder(Node* _root){if (_root == nullptr)return;_Inoder(_root->left);cout << _root->_key << ":"<<_root->_value<<endl;_Inoder(_root->right);}Node* _root;};}
两种应用场景:
void test2()
{key_value::BSTree<string, int> couttree;//key_value模型 计算水果个数string a[] = { "西瓜","香蕉","火龙果","橘子","梨子","西瓜","苹果","香蕉","火龙果" };for (auto& e : a){auto ret = couttree.FindR(e);if (ret == nullptr){couttree.insertR(e, 1);}else{ret->_value++;}}couttree.Inoder();
}
void test1()
{key_value::BSTree<string, string> dic;//查字典 key_value模型dic.insertR("insert", "插入");dic.insertR("delete", "删除");dic.insertR("love", "喜欢");dic.insertR("print", "打印");dic.Inoder();string name;while (cin >> name){auto ret = dic.FindR(name);if (ret != nullptr){cout << ret->_value << endl;}else{cout << "不存在" << endl;}}}