地理测绘基础知识(3)-观测与遮挡

在上一篇文章中，我们介绍了椭球模型下的一系列基础的坐标操作。本节，介绍观测与遮挡问题。

观测主要用于从观察点A观测大地标准点B，用来解决观测的仰角、方位角与大地坐标系之间的关系。
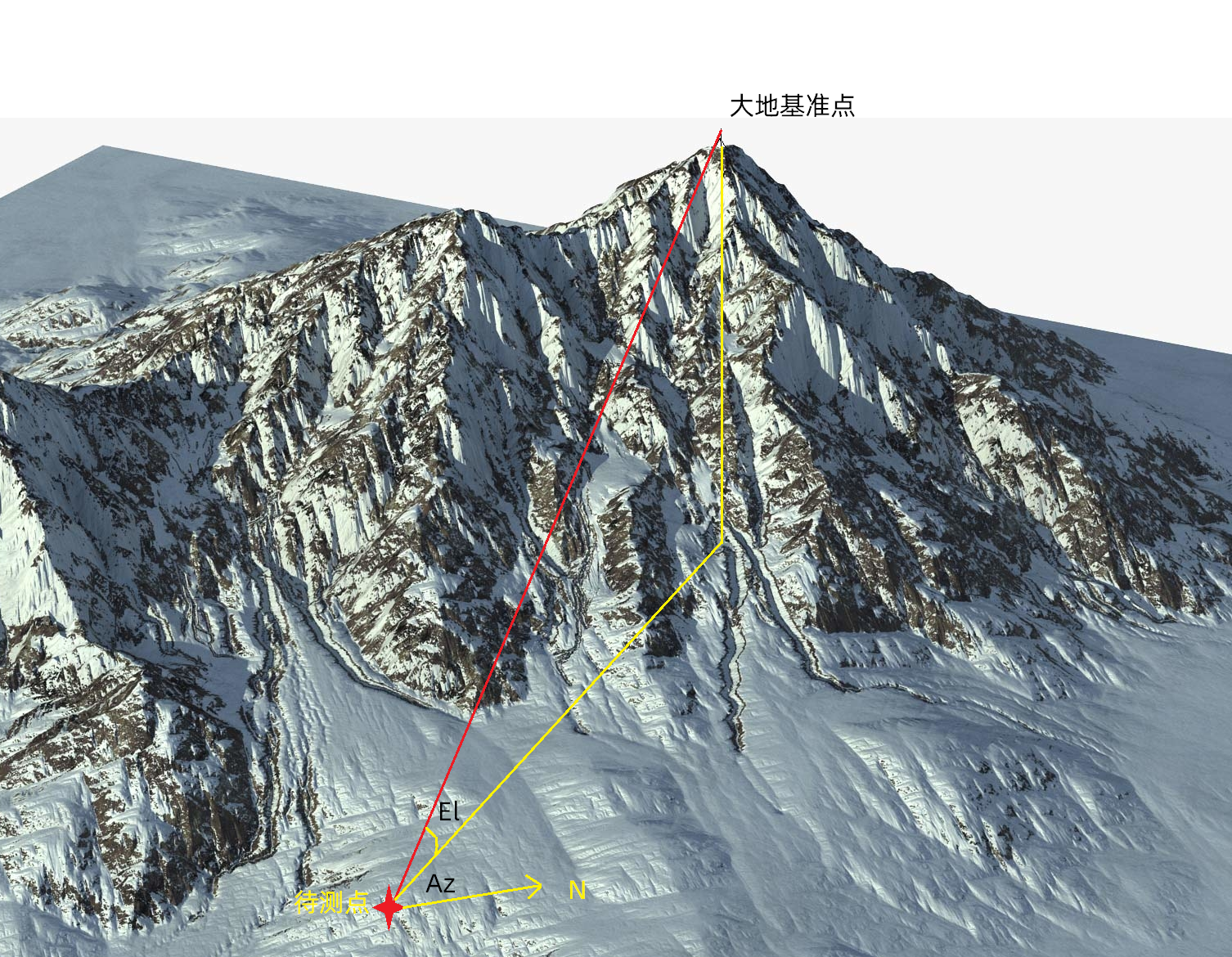在这里插入图片描述在没有GPS卫星的时代，为了测量一个位置的坐标，往往会设置多个采样点，不断测角、测距、测气压，“跑断腿”。在现代，这种基于方位俯仰的测量技术已经用的不多了，但方位俯仰的计算还是很有用的。

遮挡问题和观测是同一个问题，解决的是从A点能不能看到B的问题。有时候计算A,B的共视问题时用的很多，尤其是其中一方为高山或者飞机时。

1 根据AB两点位置求取方位角、俯仰角

在 A 点观测B点的方位俯仰，是在A点的ENU坐标下完成的。

ENU
接前文，A的ECEF坐标为 $\vec A$ , B的ECEF坐标为 $\vec B$ , 在A的ENU坐标系下的坐标为 $\vec{B_{ENU}}$ ，他们的关系：

要计算站在t位置下，查看任意一点 M 的 ENU 坐标，只要执行运算

$\vec {B_{ENU}}^T=\begin{bmatrix} {\vec {E} \\ \vec N \\ \vec U}\end{bmatrix} \times \left ( \vec {B_{ECEF}} - \vec t \right )^T =R \times \left ( \vec {B_{ECEF}} - \vec t \right )^T$

为了行文方便，重复一下R矩阵的特点。上式中坐标都是行向量,转置后是列向量。R的左逆、右逆都是自身的转置,故而两类坐标的转换很方便。如果是求取单位向量，则把 $\vec t$ 设置为0即可。

$\begin{bmatrix} {-\sin \theta} & {\cos \theta} & 0\\ {-\sin \varphi cos\theta} & {-\sin \varphi \sin \theta} & {\cos \varphi} \\ \cos \varphi cos\theta & \cos \varphi \sin \theta & \sin \varphi \end{bmatrix}$

$R\times R^T=R^T \times R=I$

(1) 俯仰El

$\sin^{-1} \frac{U}{\left| \vec {B_{ENU}}\right|}$

(2) 方位Az

$\tan^{-1} \frac{E}{N}$

(3) 基于大气折射的俯仰修正

对于大气层外的B位置，还需要考虑电磁波的折射问题。我们参考 http://www.zeptomoby.com/satellites/ 中的代码，其修正原理如下：

#ifdef WANT_ATMOSPHERIC_CORRECTIONdouble saveEl = el;// Elevation correction for atmospheric refraction.// Reference:  Astronomical Algorithms by Jean Meeus, pp. 101-104// Note:  Correction is meaningless when apparent elevation is below horizonel += deg2rad((1.02 / tan(deg2rad(rad2deg(el) + 10.3 / (rad2deg(el) + 5.11)))) / 60.0);if (el < 0.0){// Reset to true elevationel = saveEl;}if (el > (PI / 2)){el = (PI / 2);}
#endif

主要接口：

/*!* \brief observe_az_el_range	  计算方位角、俯仰角* \param llaA_in	A点(观察者)* \param llaB_in	B点(被观察者)* \param paz		方位角* \param pel		俯仰角* \param prange	长度* \param ATMOSPHERIC_CORRECTION	大气折射矫正开关* \param rad		经纬度采用弧度* \param latfirst	纬度在第一维度[0]*/
inline void observe_az_el_range(const double llaA_in[/*3*/],const double llaB_in[/*3*/],double * paz,double * pel,double * prange,bool ATMOSPHERIC_CORRECTION = false,const bool rad = false,const bool latfirst = true)

2 可视判断问题

上一节的问题，可以引申出一个命题。如果知道A\B的位置，如何判断A与B之间是不是发生遮挡？同学们有时候会想当然认为只要仰角小于0，就会遮挡。这其实只存在于A位于海面的情况。真实情况要复杂的多，和二者所处的地形有很大关系。

(1) 基于DEM的精确测算方法

一般认为：在海面上，只要A、B两点的连线与当前椭球面没有交点，则可视；在陆地上，只要A、B两点的连线与当前地形没有交点，则可视。在可视关系发生时，仰角完全可以小于0.

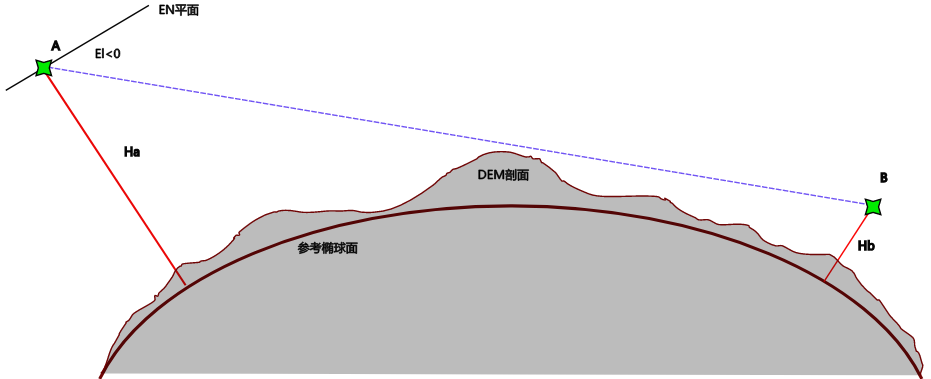
此问题可等效为线段A-B与地表数字高程DEM平面有无交点的问题。我们构造参数方程描述线段AB上的任意一点 E，游标 $\varrho$ 是介于0~1的实数。

$\vec E=\vec A + (\vec B-\vec A)\varrho$

设函数 $h=F_{dem}(\vec E)$ 能够返回ECEF坐标 $\vec E$ 对应的椭球切投影处的地面高程h（单位），而 $H=LLA_H({\vec E})$ 返回的是当前位置下的海拔，则可视的条件是：
$\forall {\varrho \in \left [0,1\right ]}: F_{dem}(\vec E)<LLA_{H}(\vec E)$
通俗的说，就是AB连线上的每一点都高于地形。

这种判断，需要有精确的数字高程数据的支持。函数F查询DEM阵列，根据经纬度网格，进行插值，获取高程。此类计算极为耗时，且与DEM数据的品类高度相关，接口上，采用functional对象进行泛化处理。

(2) 基准海平面算法

当采用标准海平面作为表面时，DEM数据恒为0. 该命题变为线段AB与椭球面有无交点的问题。可以使用斜率折半查找的方法，找到距离地面最近的参数 $\varrho$ 。

(3) 引入仰角约束

如果还有附带条件，如试图排除“擦边球”场景，避免线段上某个位置与DEM曲面恰好相切，则可以使用仰角约束。可以要求在路径上任意一点观测A、B两点的仰角均大于 $El$ ，如5度或者10度。

要注意的是，引入的约束越多，则计算越慢。

主要接口：

/*!* \brief observe_vis_judge	假设地球没有地形，是光滑的椭球，求取AB是不是可视* \param llaA_in		观测点的经纬度* \param llaB_in		被观测点经纬度* \param minEl			仰角约束，路径上所有地表位置观察A、B的仰角均要高于minEl* \param rad			经纬度采用弧度* \param latfirst		纬度在第一维度[0]* \return				true 是AB可视，false是不可视*/
inline bool observe_vis_judge(const double llaA_in[/*3*/],const double llaB_in[/*3*/],const double minEl = 0,const bool rad = false,const bool latfirst = true)；/*!* \brief observe_dem_judge 根据数字高程DEM判断可视关系* \param llaA_in	观测点的经纬度* \param llaB_in   被观测点经纬度* \param dem		数字高程回调，给入纬度（度）、经度（度），返回高度（米）* \param dem_in_meters dem数据的分辨率（米）,将使用高于1/2分辨率的精度进行搜索测试* \param minEl			仰角约束，路径上所有地表位置观察A、B的仰角均要高于minEl* \param rad		经纬度采用弧度* \param latfirst	纬度在第一维度[0]* \return			true 是AB可视，false是不可视*/
inline bool observe_dem_judge(const double llaA_in[/*3*/],const double llaB_in[/*3*/],std::function<double (double lat,double lon)> dem,const double dem_in_meters,const double minEl = 0,const bool rad = false,const bool latfirst = true)；