目录
- 前言
- 泛读
- 摘要
- Introduction
- Related Work
- 小结
- 精读
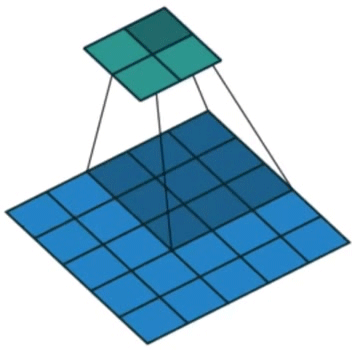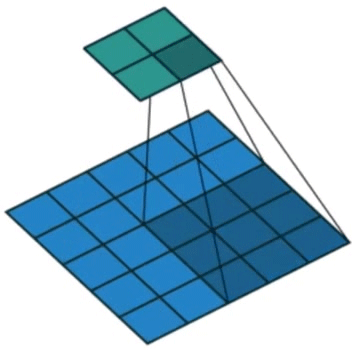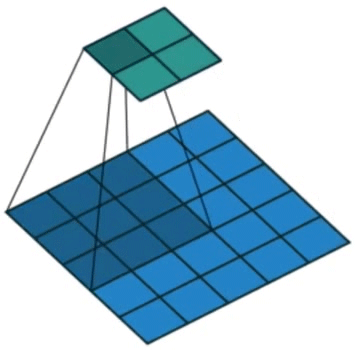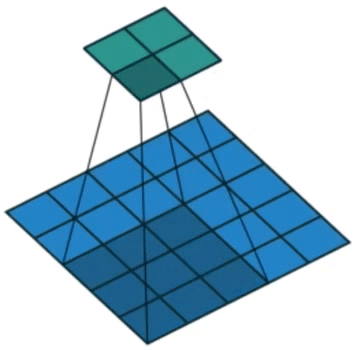
- 编码器:特征卷积
- 解码器:LSTM网络
- 随机硬注意力和确定软注意力机制
- 硬注意力
- 软注意力
- 双重随机注意力
- 训练
- 实验
- 数据集
- 评估过程
- 定量分析
- 定性分析
- 结论
- 代码(略)
前言
本课程来自深度之眼《多模态》训练营,部分截图来自课程视频。
文章标题:how, Attend and Tell: Neural Image Caption Generation with Visual Attention
神经图像描述生成
作者:Kelvin Xu等
单位:多伦多+蒙特利尔大学
发表时间:2015 ICML
Latex 公式编辑器
泛读
本文使用CNN提取图像特征,将Softmax层之前的那一层vector作为encoder端的输出并送入decoder中,使用LSTM对其解码并生成句子,这种方法也是本文所采取的方法,只是在此基础上嵌入了soft和hard attention机制。
摘要
Inspired by recent work in machine translation and object detection, we introduce an attention based model that automatically learns to describe the content of images.
第一句,总体描述,黑体部分破题:基于注意力的模型
We describe how we can train this model in a deterministic manner using standard backpropagation techniques and stochastically by maximizing a variational lower bound.
我们。。。
We also show through visualization how the model is able to automatically learn to fix its gaze on salient objects while generating the corresponding words in the output sequence.
我们还。。。(这部分工作是重点)
We validate the use of attention with state-of-the-art performance on three benchmark datasets: Flickr8k, Flickr30k and MS COCO.
SOTA描述
Introduction
自动生成图像的标题是一项与场景理解的核心非常接近的任务——计算机视觉的主要目标之一。标题生成模型不仅必须强大到足以解决计算机视觉的挑战,即确定哪些物体在图像中,而且它们还必须能够捕捉并以自然语言表达它们的关系。由于这个原因,标题生成长期以来一直被视为一个困难的问题。对于机器学习算法来说,这是一个非常重要的挑战,因为它相当于模仿人类将大量突出的视觉信息压缩成描述性语言的非凡能力。
第二段大概讲了一下前人的工作,并表示现在流行的做法是CNN+RNN,然后将在下一节进行展开。
第三段:人类视觉系统中最引人入胜的一面是注意力的存在。注意力不是将整个图像压缩成一个静态的表示,而是允许突出的特征在需要时动态地出现在最前面。当图像中存在大量的杂乱无章的信息时,这一点尤其重要。使用表征(如来自convnet顶层的表征),将图像中的信息提炼成最突出的对象,是一种有效的解决方案,在以前的工作中被广泛采用。不幸的是,这有一个潜在的缺点,即失去了可能对更丰富、更有描述性的标题有用的信息。使用更多的低层次表示法可以帮助保留这些信息。然而,使用这些特征需要一个强大的机制来引导模型,以获得对当前任务重要的信息。
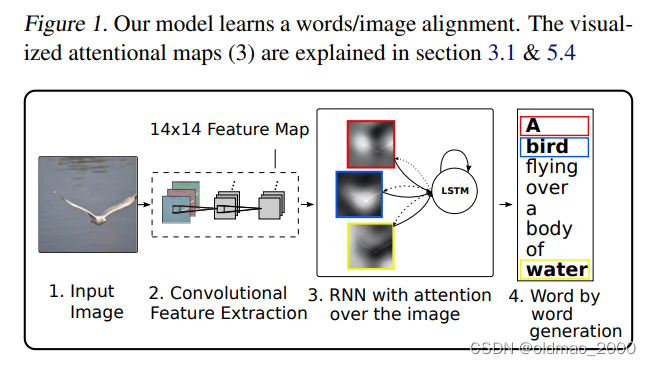
接下来开始写本文的工作:
使用从卷积网络的顶层提取图像信息到最显著地对象的表示。但是缺点是容易丢失对描述标题更有用的信息,使用低级表示有助于保存信息。
除了神经网络之外,image caption还有两种典型的方法:
1、使用模板的方法,填入一些图像中的物体;
2、使用检索的方法,寻找相似描述。
这两种方法都使用了一种泛化的手段,使得描述跟图片很接近,但又不是很准确。所以作者在此基础上提出了自己的模型架构,将soft和hard attention引入到caption,并利用可视化手段理解attention机制的效果。
最后一段具体讲本文contribution以及文章的section构成:
我们在一个通用框架(第3.1节)中引入了两种基于注意力的图像caption生成器:
1)一种可通过标准反向传播方法训练的“软”确定性注意力机制;
2)一种可通过以下方法训练的“硬”随机注意力机制用REINFORCE最大化或等效地最大化近似下限(Williams,1992)。
我们展示了如何通过可视化关注的重点在“何处”和“何处”来获得洞察力并解释该框架的结果,定量地验证了注意力在字幕生成中的作用和最新的表现。(第5.4节)
最后,我们在以下三个基准数据集上以最先进的性能(第5.3节)定量验证了注意力在caption生成中的有用性:Flickr8k,Flickr30k,和 MS COCO数据集。
“soft” deterministic attention mechanism 确定性注意力机制:确定的全局注意力
“hard” stochastic attention mechanism 随机注意力机制:不确定取attention的区域位置
本文主要提出了与soft attention相对应的hard attention
•hard: Attention每次移动到一个固定大小的区域(类似句子中我只关注主语部分)
•soft: Attention每次是所有区域的一个加权和(每个单词都和其他所以单词进行注意力计算,自己决定当前单词和其他单词的紧密关系,是全局的,自动的)
soft attention是可微的,即attention项和作为结果的loss function都是输入的可微函数,这样梯度信息保留下来,就可以进行反向传播。
图2中展示了注意力随着词序变化的情况:

图3表示了不同图片中注意力的区域:

Related Work
在这一节中,我们提供了以前关于图像描述生成和注意力机制的相关背景。最近,人们提出了几种生成图像描述的方法。其中许多方法都是基于递归神经网络,并受到成功使用神经网络进行机器翻译的序列到序列训练的启发。图像标题生成非常适合机器翻译的编码器-解码器框架的一个主要原因是它类似于将图像 "翻译 "成句子。
第一个使用神经网络来生成标题的方法是Kiros等人(2014a),他们提出了一个多模态的对数线性模型,该模型由图像的特征来偏重。这项工作后来由Kiros等人(2014b)跟进,其方法被设计为明确地允许以自然的方式进行排名和生成。Mao等人(2014)采取了类似的生成方法,但用一个递归的神经语言模型取代了前馈的神经语言模型。Vinyals等人(2014)和Donahue等人(2014)的模型都使用LSTM RNNs。与Kiros等人(2014a)和Mao等人(2014)的模型在输出词序列的每个时间步骤都看到图像不同,Vinyals等人(2014)只在开始时向RNN展示图像。在图像方面,Donahue等人也将LSTMs应用于视频,使他们的模型能够生成视频描述。
然后下一段开始评述模式:
所有这些工作都将图像表示为来自预先训练的卷积网络顶层的单一特征向量。Karpathy和Li则提出了学习一个用于排名和生成的联合嵌入空间,其模型学习将句子和图像的相似性作为双向RNN输出的R-CNN对象检测的一个函数来评分。这里提到其实是CLIP的工作。
Fang 等人(2014 年)提出了一种通过结合物体检测进行生成的三步管道。他们的模型首先基于多实例学习框架学习多个视觉概念的检测器。然后将在caption上训练的语言模型应用于检测器的输出,然后从联合图像-文本嵌入空间进行重构。
与这些模型不同的是,我们提出的注意力框架没有明确地使用物体检测器,而是从头开始学习潜在的排列组合。这使我们的模型能够超越 “对象性”,并学会关注抽象的概念。
在使用神经网络生成caption之前,有两种主要方法占主导地位。第一种方法是生成caption模板,根据对象检测和属性发现的结果进行填充;第二种方法是首先从一个大型数据库中检索类似的caption图片,然后修改这些检索到的caption以适应查询。这些方法通常涉及一个中间的 "泛化 "步骤,以去除caption中只与检索到的图像相关的细节,如城市的名称等。这两种方法后来都被现在占主导地位的(端到端)神经网络方法淘汰了。
小结
本文目的: Study the attention mechanism used in natural image caption algorithm.
研究目标: Models with an attention mechanism can attend to the salient part of an image while generating its caption.
精读
编码器:特征卷积
我们的模型使用单个原始图像生成caption: y \text{y} y,该caption y \text{y} y为1-of- K K K个的编码序列。
y = { y 1 , ⋯ , y C } , y i ∈ R K y=\{\text{y}_1,\cdots,\text{y}_C\},\text{y}_i\in\mathbb{R}^K y={y1,⋯,yC},yi∈RK
其中 K K K是词库大小, C C C是caption的长度。我们使用卷积神经网络来提取一组特征向量,命名为 a \text{a} a,我们将其称为注释向量。 提取器产生 L L L个特征向量,每个 D D D维向量对应于图像的一部分。
a = { a 1 , ⋯ , a L } , a i ∈ R D a=\{\text{a}_1,\cdots,\text{a}_L\},\text{a}_i\in\mathbb{R}^D a={a1,⋯,aL},ai∈RD
a i \text{a}_i ai是一个D维特征,共有 L L L个,描述图像的 L L L个不同区域(可重叠)。这里使用CNN对图像进行特征提取,使用较低卷积层提取特征(之前的研究使用全连接层,而这里为了获得特征向量和二维图像各部分之间的对应关系,使用的是 lower convolutional layer),允许解码器通过选择所有特征向量的子集来选择性地聚焦于图像的某些部分。
解码器:LSTM网络
LSTM网络(如图4)通过在上下文向量,先前的隐藏状态和先前生成的单词的条件下的每个时间步生成一个单词来产生CAPTION。
使用 T s , t : R s → R t T_{s,t}:\mathbb{R}^s\rightarrow\mathbb{R}^t Ts,t:Rs→Rt表示具有所学习参数的简单仿射变换
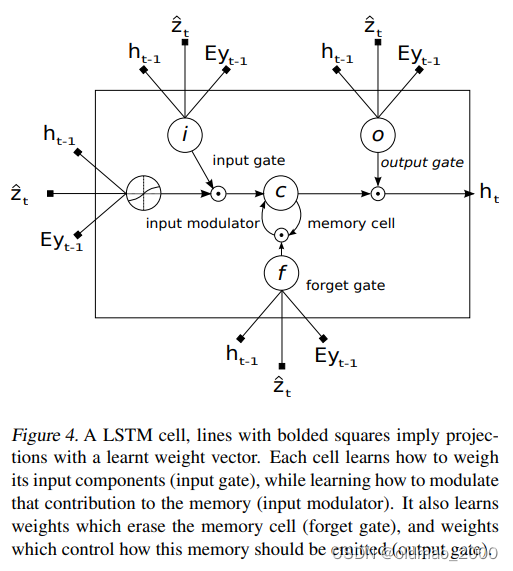
( i t f t o t g t ) = ( σ σ σ tanh ) T D + m + n , n ( E y t − 1 h t − 1 z t ^ ) c t = f t ⊙ c t − 1 + i t ⊙ g t h t = o t ⊙ tanh ( c t ) \begin{pmatrix} i_t \\ f_t \\ o_t \\ g_t\end{pmatrix}= \begin{pmatrix} \sigma \\ \sigma \\ \sigma \\ \tanh\end{pmatrix}T_{D+m+n,n} \begin{pmatrix} E_{y_{t-1}} \\ h_{t-1} \\ \hat{z_t} \\ \end{pmatrix}\\ c_t = f_t\odot c_{t-1}+i_t\odot g_t\\ h_t=o_t\odot \tanh(c_t) itftotgt = σσσtanh TD+m+n,n Eyt−1ht−1zt^ ct=ft⊙ct−1+it⊙gtht=ot⊙tanh(ct)
公式中 i t , f t , c t , o t , h t i_t,f_t,c_t,o_t,h_t it,ft,ct,ot,ht分别是LSTM的输入状态,忘记状态,存储状态,输出状态和隐藏状态。
向量 z ^ ∈ R D \hat{z}\in\mathbb{R}^D z^∈RD是上下文向量,捕获与特定输入位置相关的视觉信息。
E ∈ R m × K E\in \mathbb{R}^{m×K} E∈Rm×K是一个嵌入矩阵。
m和n分别表示嵌入和LSTM维度
σ和 ⊙ \odot ⊙分别表示sigmoid和逐元素乘法。
上式中的上下文向量 z t ^ \hat{z_t} zt^是在时间t输入的图像相关部分的动态表示。我们定义了一种机制 ϕ \phi ϕ,它可以从注释矢量 a i , i = 1 ⋯ L \text{a}_i,i= 1\cdots L ai,i=1⋯L计算 z t ^ \hat{z_t} zt^, L L L对应于在不同图像位置处提取的特征。对于每个位置 i i i,该机制都会产生正权重 α i α_i αi,它可以解释为位置 i i i是产生下一个单词的正确焦点所在的可能性(“硬”注意力:随机的注意力机制),也可以解释为 i i i位置在 a i \text{a}_i ai中的相对重要性。每个注释向量 a i \text{a}_i ai的权重 α i α_i αi是由注意力模型 f a t t f_{att} fatt计算得出的,为此我们使用了基于先前隐藏的多层感知器(MLP)状态 h t − 1 \text{h}_{t-1} ht−1。
e t i = f a t t ( a i , h t − 1 ) α t i = e x p ( e t i ) ∑ k = 1 L exp ( e t k ) e_{ti}=f_{att}(\text{a}_i,\text{h}_{t-1})\\ \alpha_{ti}=\cfrac{exp(e_{ti})}{\sum_{k=1}^L \exp(e_{tk})} eti=fatt(ai,ht−1)αti=∑k=1Lexp(etk)exp(eti)
软注意力机制使用的是Bahdanau等人模型 。我们注意到隐藏状态随输出RNN的输出顺序的前进而变化:网络下一步查找的“位置”取决于已生成的单词的顺序。
计算出权重 α i α_i αi(通过softmax后总和为1)后,可通过以下公式计算上下文向量 z t ^ \hat{z_t} zt^:
z t ^ = ϕ ( { a i } , { α i } ) \hat{z_t}=\phi (\{\text{a}_i\},\{α_i\}) zt^=ϕ({ai},{αi})
其中, ϕ \phi ϕ是在给定注释矢量及其相应权重的情况下返回单个矢量的函数。 ϕ \phi ϕ函数的详细内容将在第二节中讨论。
LSTM的初始内存状态和隐藏状态由通过两个单独的MLP馈送的注释向量的平均值来预测:
c 0 = f init,c ( 1 L ∑ i L a i ) h 0 = f init,h ( 1 L ∑ i L a i ) \text{c}_0=f_{\text{init,c}}(\cfrac{1}{L}\sum_i^L \text{a}_i)\\ \text{h}_0=f_{\text{init,h}}(\cfrac{1}{L}\sum_i^L \text{a}_i) c0=finit,c(L1i∑Lai)h0=finit,h(L1i∑Lai)
本文使用一个深层输出层(Pascanu等人,2014)在给定LSTM状态,上下文向量和前一个单词的情况下计算输出单词概率:
p ( y t ∣ a , y 1 t − 1 ) ∝ exp ( L o ( E y t − 1 + L h h t + L z z ^ t ) ) p(\text{y}_t|\text{a},\text{y}_1^{t-1})\propto\exp(\text{L}_o(\text{E}{\text{y}_{t-1}}+\text{L}_h\text{h}_t+\text{L}_z\hat{\text{z}}_t)) p(yt∣a,y1t−1)∝exp(Lo(Eyt−1+Lhht+Lzz^t))
其中 L o ∈ R K × m , L h ∈ R m × m , L z ∈ R m × D \text{L}_o\in\mathbb{R}^{K\times m},\text{L}_h\in\mathbb{R}^{m\times m},\text{L}_z\in\mathbb{R}^{m\times D} Lo∈RK×m,Lh∈Rm×m,Lz∈Rm×D
E E E是随机初始化的学习参数
随机硬注意力和确定软注意力机制
stochastic attention and deterministic attention
硬注意力
我们将位置变量 s t s_t st表示为模型在生成第 t t t个字时决定集中注意力的位置。 s t , i s_{t,i} st,i是指示符(独热编码),如果第i个位置( L L L除外)是用于提取视觉特征的位置,则将其设置为1。 通过将注意力位置视为中间潜变量,我们可以分配一个由 { α i } \{α_i\} {αi}参数化的多重分布,并将 z ^ t \hat z_t z^t视为随机变量:
p ( s t , i = 1 ∣ s j < t , a ) = α t , i z ^ t = ∑ i s t , i a i p(s_{t,i}=1|s_{j<t},\text{a})=\alpha_{t,i}\\ \hat {\text{z}}_t=\sum_is_{t,i}\text{a}_i p(st,i=1∣sj<t,a)=αt,iz^t=i∑st,iai
我们定义了一个新的目标函数 L s L_s Ls,该函数是边际对数似然 log p ( y ∣ a ) \log p(\text{y}|\text{a}) logp(y∣a)的变分下界,该对数观察给定图像特征 a \text{a} a的单词 y \text{y} y的序列。 可以通过直接优化 L s L_s Ls得出模型参数 W W W的学习算法:
L s = ∑ s p ( s ∣ a ) log p ( y ∣ s , a ) ≤ log ∑ s p ( s ∣ a ) p ( y ∣ s , a ) = log p ( y ∣ a ) L_s=\sum_s p(s|\text{a})\log p(\text{y}|s,\text{a})\leq \log\sum_s p(s|\text{a}) p(\text{y}|s,\text{a})=\log p(\text{y}|\text{a}) Ls=s∑p(s∣a)logp(y∣s,a)≤logs∑p(s∣a)p(y∣s,a)=logp(y∣a)
参数 W W W的偏导公式如下:
∂ L s ∂ W = ∑ s p ( s ∣ a ) [ ∂ log p ( y ∣ s , a ) ∂ W + log p ( y ∣ s , a ) ∂ log p ( s ∣ a ) ∂ W ] \cfrac{\partial L_s}{\partial W}=\sum_sp(s|\text{a})\left [\cfrac{\partial \log p(\text{y}|s,\text{a})}{\partial W}+\log p(\text{y}|s,\text{a})\cfrac{\partial \log p(s|\text{a})}{\partial W}\right ] ∂W∂Ls=s∑p(s∣a)[∂W∂logp(y∣s,a)+logp(y∣s,a)∂W∂logp(s∣a)]
上式中提出了相对于模型参数的基于蒙特卡洛的近似采样。 这可以通过从上面定义的多重分布中采样位置 s t s_t st来完成:
s ~ t ∼ Multinoulli L ( { α i } ) \tilde s_t\sim\text{Multinoulli}_L(\{α_i\}) s~t∼MultinoulliL({αi})
∂ L s ∂ W ≈ 1 N ∑ n = 1 N [ ∂ log p ( y ∣ s ~ n , a ) ∂ W + log p ( y ∣ s ~ n , a ) ∂ log p ( s ~ n ∣ a ) ∂ W ] \cfrac{\partial L_s}{\partial W}\approx \cfrac{1}{N}\sum_{n=1}^N\left [\cfrac{\partial \log p(\text{y}|\tilde s^n,\text{a})}{\partial W}+\log p(\text{y}|\tilde s^n,\text{a})\cfrac{\partial \log p(\tilde s^n|\text{a})}{\partial W}\right ] ∂W∂Ls≈N1n=1∑N[∂W∂logp(y∣s~n,a)+logp(y∣s~n,a)∂W∂logp(s~n∣a)]
借鉴Weaver&Tao使用移动平均基线来减少梯度的蒙特卡洛估计器中的方差。 Mnih等人先前
已使用类似但更复杂的方差减少技术。 看到第k个mini-batch后,将移动平均基线估计为先前对数似然具有指数衰减的累积总和:
b k = 0.9 × b k − 1 + 0.1 × log p ( s ~ k ∣ a ) b_k=0.9\times b_{k-1}+0.1\times \log p(\tilde s_k|\text{a}) bk=0.9×bk−1+0.1×logp(s~k∣a)
为了进一步减少估计量方差,在多重分布 H [ s ] H[s] H[s]上添加了一个熵项。 同样,对于给定图像,概率为0.5,我们将采样的注意力位置 s ~ \tilde s s~设置为其期望值 α α α。 两种技术都提高了随机注意力学习算法的鲁棒性。 该模型的最终学习规则如下
∂ L s ∂ W ≈ 1 N ∑ n = 1 N [ ∂ log p ( y ∣ s ~ n , a ) ∂ W + λ r ( log p ( y ∣ s ~ n , a ) − b ) ∂ log p ( s ~ n ∣ a ) ∂ W + λ e ∂ H [ s ~ n ] ∂ W ] \cfrac{\partial L_s}{\partial W}\approx \cfrac{1}{N}\sum_{n=1}^N\left [\cfrac{\partial \log p(\text{y}|\tilde s^n,\text{a})}{\partial W}+\lambda_r(\log p(\text{y}|\tilde s^n,\text{a})-b)\cfrac{\partial \log p(\tilde s^n|\text{a})}{\partial W}+\lambda_e\cfrac{\partial H[\tilde s^n]}{\partial W}\right ] ∂W∂Ls≈N1n=1∑N[∂W∂logp(y∣s~n,a)+λr(logp(y∣s~n,a)−b)∂W∂logp(s~n∣a)+λe∂W∂H[s~n]]
λ r , λ e \lambda_r,\lambda_e λr,λe是通过交叉验证设置的两个超参数。有研究指出,上式等效于REINFORCE学习规则的公式(Williams,1992年),其中注意力机制选择行动序列的奖励是与采样注意轨迹下目标句子的对数似然成正比的实数值。
the reward for the attention choosing a sequence of actions is a real value proportional to the log likelihood of the target sentence under the sampled attention trajectory.
注意力选择一连串action的reward是一个实值,与目标句子在采样注意力轨迹下的对数可能性成正比。
在对每个点进行硬选择时, ϕ ( { a i } , { α i } ) \phi(\{\text{a}_i\},\{α_i\}) ϕ({ai},{αi})是一个函数,该函数基于由 α α α参数化的多元分布在每个时间点返回采样的 a i \text{a}_i ai
软注意力
学习随机注意力需要每次对关注位置 s t s_t st进行采样,等价的来说,我们可以直接获取上下文向量 z ^ t \hat{\text{z}}^t z^t的期望值:
E p ( s t ∣ a ) [ z ^ t ] = ∑ i = 1 L α t , i a i \mathbb{E}_{p(s_t|a)}[\hat{\text{z}}^t]=\sum_{i=1}^L\alpha_{t,i}\text{a}_i Ep(st∣a)[z^t]=i=1∑Lαt,iai
并通过计算软注意力加权加权注释向量 ϕ ( { a i } , { α i } ) = ∑ i L α i a i \phi(\{\text{a}_i\},\{α_i\})=\sum_{i}^L\alpha_{i}\text{a}_i ϕ({ai},{αi})=∑iLαiai来确定确定性注意力模型。由于软注意力计算连续可微,因此可以使用端到端的方式进行反向传播训练。
学习软注意力也可以理解为注意力位置随机变量 s t s_t st下近似优化 L s L_s Ls方程中的边际可能性。
LSTM的隐藏激活函数 h t h_t ht是随机上下文向量 z ^ t \hat{\text{z}}^t z^t的线性投影,丢进非线性函数tanh中。
对于一阶Taylor逼近,期望值 E p ( s t ∣ a ) [ h t ] \mathbb{E}_{p(s_t|a)}[{\text{h}}_t] Ep(st∣a)[ht]等于使用预期上下文向量 E p ( s t ∣ a ) [ z ^ t ] \mathbb{E}_{p(s_t|a)}[\hat{\text{z}}^t] Ep(st∣a)[z^t]进行单前向传播后计算的 h t \text{h}_t ht。
考虑到之前计算上下文向量和前一个单词的情况下计算输出单词概率公式:
p ( y t ∣ a , y 1 t − 1 ) ∝ exp ( L o ( E y t − 1 + L h h t + L z z ^ t ) ) p(\text{y}_t|\text{a},\text{y}_1^{t-1})\propto\exp(\text{L}_o(\text{E}{\text{y}_{t-1}}+\text{L}_h\text{h}_t+\text{L}_z\hat{\text{z}}_t)) p(yt∣a,y1t−1)∝exp(Lo(Eyt−1+Lhht+Lzz^t))
令
n t = L o ( E y t − 1 + L h h t + L z z ^ t ) \text{n}_t=\text{L}_o(\text{E}{\text{y}_{t-1}}+\text{L}_h\text{h}_t+\text{L}_z\hat{\text{z}}_t) nt=Lo(Eyt−1+Lhht+Lzz^t)
n t , i n_{t,i} nt,i表示通过将随机变量 z ^ \hat{\text{z}} z^值设定为 a i \text{a}_i ai而计算出的 n t \text{n}_t nt。
我们为softmax k t h k^{th} kth词预测定义归一化的加权几何平均值为:
N W G M [ p ( y t = k ∣ a ) ] = ∏ i exp ( n t , k , i ) p ( s t , i = 1 ∣ a ) ∑ j ∏ i exp ( n t , j , i ) p ( s t , i = 1 ∣ a ) = exp ( E p ( s t ∣ a ) [ n t , k ] ) ∑ j exp ( E p ( s t ∣ a ) [ n t , j ] ) NWGM[p(y_t=k|\text{a})]=\cfrac{\prod_i\exp(n_{t,k,i})^{p(s_{t,i=1}|a)}}{\sum_j\prod_i\exp(n_{t,j,i})^{p(s_{t,i=1}|a)}}\\ =\cfrac{\exp(\mathbb{E}_{p(s_t|a)}[n_{t,k}])}{\sum_j\exp(\mathbb{E}_{p(s_t|a)}[n_{t,j}])} NWGM[p(yt=k∣a)]=∑j∏iexp(nt,j,i)p(st,i=1∣a)∏iexp(nt,k,i)p(st,i=1∣a)=∑jexp(Ep(st∣a)[nt,j])exp(Ep(st∣a)[nt,k])
上面的等式表明,使用预期的上下文向量可以很好地逼近caption预测的标准化加权几何平均值,其中
E [ n t ] = L o ( E y t − 1 + L h E [ h t ] + L z E [ z ^ t ] ) \mathbb{E}[\text{n}_t]=\text{L}_o(\text{E}{\text{y}_{t-1}}+\text{L}_h\mathbb{E}[\text{h}_t]+\text{L}_z\mathbb{E}[\hat{\text{z}}_t]) E[nt]=Lo(Eyt−1+LhE[ht]+LzE[z^t])
它表明softmax单元的NWGM是通过将softmax应用于基本线性投影的期望值而获得的。 另外,根据(Baldi&Sadowski,2014)的结果,在softmax激活下, N W G M [ p ( y t = k ∣ a ) ] ≈ E [ p ( y t = k ∣ a ) ] NWGM[p(y_t=k|\text{a})]\approx\mathbb{E}[p(y_t=k|\text{a})] NWGM[p(yt=k∣a)]≈E[p(yt=k∣a)]。 这意味着由随机变量 s t s_t st引起
的所有可能的注意力位置上的输出期望值,是通过预期上下文向量 E [ z ^ t ] \mathbb{E}[\hat{\text{z}}^t] E[z^t]进行简单的前向传播计算。 换句话说,软注意力模型是注意力位置上的边缘似然性(marginal likelihood)的近似值。
双重随机注意力
通过构造, ∑ i α t i = 1 \sum_i\alpha_{ti}=1 ∑iαti=1(因为它们是oftmax的输出)。 在训练模型的确定性版本(硬注意力)时,我们引入了一种双重随机随机正则化形式,其中我们还鼓励 ∑ t α t i ≈ 1 \sum_t\alpha_{ti}\approx1 ∑tαti≈1。这可以解释为鼓励模型在生成过程中对图像的每个部分给予同等的关注。 在我们的实验中,我们观察到从数量上看,这种正则化对提高整体BLEU分数很重要,并且从质量上讲,这会导致caption更加丰富和描述性。 另外,软注意力模型在每个时间步长 t t t处从先前的隐藏状态 h t − 1 \text{h}_{t-1} ht−1预测门控标量 β β β,使得 ϕ ( { a i } , { α i } ) = β ∑ i L α i a i \phi(\{\text{a}_i\},\{α_i\})=\beta\sum_i^L\alpha_i\text{a}_i ϕ({ai},{αi})=β∑iLαiai,其中 β t = σ ( f β ( h t − 1 ) ) \beta_t=\sigma(f_{\beta}(\text{h}_{t-1})) βt=σ(fβ(ht−1))。 我们注意到我们的注意力权重通过包含标量β来更加强调图像中的对象。
具体而言,模型通过最小化以下不利的对数似然性来对模型进行端到端训练:
L d = − log ( P ( y ∣ x ) ) + λ ∑ i L ( 1 − ∑ t C α t i ) 2 L_d=-\log(P(\text{y}|\text{x}))+\lambda\sum_i^L(1-\sum_t^C\alpha_{ti})^2 Ld=−log(P(y∣x))+λi∑L(1−t∑Cαti)2
训练
我们的注意力模型的两个变体(软、硬)都使用自适应学习率算法进行了随机梯度下降训练。 对于Flickr8k数据集,我们发现RM-SProp(Tieleman&Hinton,2012)效果最佳,而对于Flickr30k/MS COCO数据集,我们使用了最近提出的Adam算法(Kingma&Ba,2014)。
为了创建解码器使用的注释 a i a_i ai,我们使用了在ImageNet上进行预训练的Oxford VGGnet(Simonyan&Zisserman,2014),而没有进行微调。但是原则上可以使用任何编码器(CNN)。 另外,有了足够的数据,我们还可以从零开始(或微调)训练模型的其余部分的编码器。 在我们
的实验中,我们在最大池化之前的第四个卷积层使用的是14×14×512特征图。 这意味着我们的解码器可以对196×512(即L×D)的图片进行扁平化编码操作。
由于我们的实现需要的时间与每次更新中最长句子的长度成正比,因此我们发现,对随机caption组的训练在计算上是浪费的。 为了减轻这个问题,在预处理中,我们构建了一个字典,将句子的长度映射到相应的caption子集。 然后,在训练过程中,我们随机取样一个长度,并检索该长度的大小为64的mini-batch。 我们发现,这大大提高了收敛速度,而性能却没有明显下降。 在我们最大的数据集(MS COCO)上,我们的软注意力模型花费不到3天的时间在NVIDIA Titan Black GPU上进行训练。
除了抓爆外(Srivastava等,2014),我们使用的唯一其他正则化策略是early stopping(跑BLEU评分过程)。在实验的后期训练中,我们观察到验证集对数似然性与BLEU之间的相关性差异很大。 由于BLEU是最常报告的指标,因此我们在验证集上使用了BLEU进行模型选择。在我们的实验中,我们在Flickr8k实验中还使用了Whet-lab(Snoek等人,2012; 2014)。 有一些超参数的设置是在Flickr30k和COCO实验中搞定的。
我们将基于Theano的这些模型的代码(Bergstra等,2010)公开发布,以鼓励该领域的进一步研究。
实验
数据集
我们报告了流行的Flickr8k和Flickr30k数据集的结果,两个数据集分别具有8,000和30,000图像,以及更具挑战性的Microsoft COCO数据集具有82,783图像。 Flickr8k Flickr30k数据集每个图像都带有5个参考语句,但是对于MS COCO数据集,某些图像的引用量超过5个,以确保我们丢弃的数据集的一致性。 我们仅对MS COCO应用了基本标记,因此它与Flickr8k和Flickr30k中存在的标记一致。对于我们所有的实验,我们使用的固定词汇量为10,000。
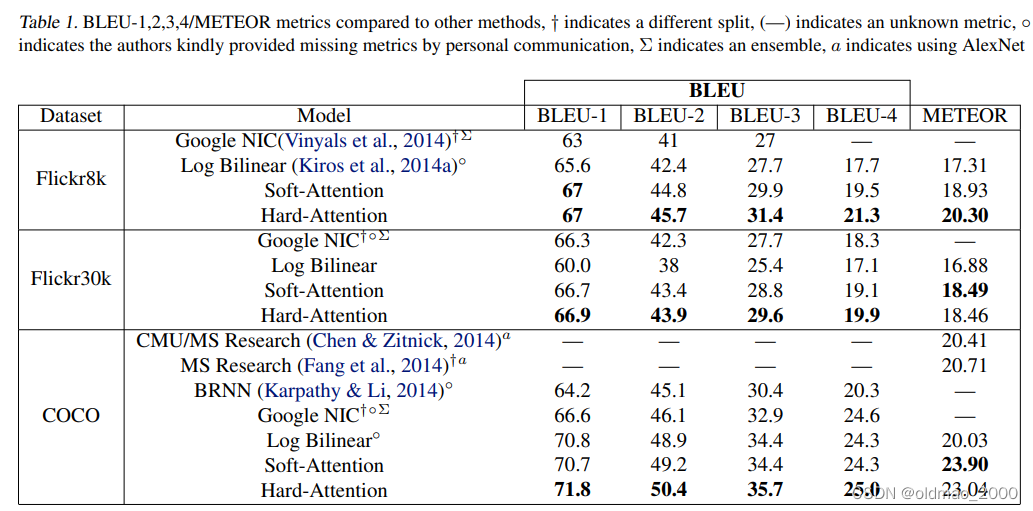
上表报告了基于关注的体系结构的结果。 我们使用常用的BLEU metric2报告结果,这是caption生成文献中的标准。 我们报告BLEU从1到4,但没有brevity penalty(BLEU 中的某个惩罚因子)。 但是,由于有研究人员对BLEU提出了批评,因此我们还报告了另一种常见的METEOR标准(Denkowski&Lavie,2014年),并在可能的情况下进行比较。
评估过程
对评估过程的影响因素进行一些说明:
首先是卷积特征提取器选择的差异。 对于相同的解码器架构,请使用最新的架构,例如GoogLeNet或Ox-ford VGG Szegedy等。(2014),Simonyan&Zisserman(2014)可
以比使用AlexNet带来更高的性能(Krizhevsky et al。,2012)。 在我们的评估中,我们仅直接与使用可比的GoogLeNet / Oxford VGG功能的结果进行比较,但是对于METEOR指标的评估比较,我们则使用AlexNet的结果。
第二个挑战是单一模型与整体比较。 虽然其他方法通过使用集成(ensemble)得到了性能提升,但在我们的结果中,我们报告了单个模型的性能。
最后,由于数据集拆分之间的差异。 在我们报告的结果中,我们使用Flickr8k的预定义拆分。 但是,Flickr30k和COCO数据集的挑战之一是缺乏标准化的分割。 本文报告了先前工作中使用的公开可用拆分(Karpathy&Li,2014,第一篇文章)。 根据我们的经验,拆分的差异不会对整体性能产生实质性的影响,但是我们注意到存在差异的地方。
定量分析
其实就是上面那个大表,该表中,我们提供了验证注意力定量有效性的实验总结。 我们在Flickr8k,Flickr30k和MS COCO上获得了最先进的性能。 此外,我们注意到,在我们的实验中,我们能够显着改善MS COCO上的METEOR性能(SOTA),我们推测这与使用了更低层表示的某些正则化技术有关。 最后,我们还注意到,我们可以使用单个模型获得整体的性能。
定性分析
通过对模型学习到的注意力成分进行可视化,我们可以在模型的输出中增加一层解释性(见图1中的第3点)。 其他执行此操作的系统则依赖于对象检测系统来生成候选对齐目标(Karpathy&Li,2014)。 我们的方法更加灵活,因为模型可以处理“非对象”突出区域。19层的OxfordNet使用3x3过滤器堆栈,这意味着特征图尺寸在最大池化层中变小。调整输入图像的大小,以使最短的一面为256维,并保留长宽比。卷积网络的输入是中心裁剪的224x224图像。因此,在4个最大池化层的情况下,顶部卷积层的输出尺寸为14x14。因此,为了可视化软模型的注意权重,我们将权重上采样设置为 2 4 = 16 2^4 = 16 24=16倍,然后应用高斯滤波器。我们注意到,每个14x14单元的接收场高度重叠。正如我们在图2和3中看到的那样,该模型学习了与人类直觉非常吻合的对齐方式。尤其是在错误示例中,我们看到可以利用这种可视化效果来直观了解为什么会犯这些错误。我们在附录A中为读者提供了更广泛的可视化示例。
结论
我们提出了一种基于注意力的方法,该方法使用BLEU和METEOR指标在三个基准数据集上提供最新性能。 我们还展示了如何利用学习到的注意力为模型生成过程提供更多的可解释性,并证明学习到的
对齐方式非常符合人类的直觉。 我们希望本文的结果能够鼓励将来使用视觉注意力的工作。 我们还期望将编码器/解码器方法的模块化与关注结合起来,使其在其他领域中有用。